Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 03. 2018 12:09
Uspořádej čísla
Ahoj. Na internetu jsem narazila na příklad, snad zajímavý...
Uspořádej čísla 1 až 305 tak, aby součet každých dvou sousedů byl třetí mocninou celého čísla.
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#2 09. 03. 2018 17:11
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Uspořádej čísla
↑ Andrejka3:
Ahoj. A lze to? Nebo se má dokázat, že to nejde? :-)
"Máte úhel beta." "No to nemám."
Offline
#3 09. 03. 2018 17:37 — Editoval check_drummer (09. 03. 2018 21:05)
#4 09. 03. 2018 18:13
Re: Uspořádej čísla
What does a drowning number theorist say?
'log log log log ...'
Offline
#5 10. 03. 2018 14:57
Re: Uspořádej čísla
Řešení je tady, bez komentáře, jak k němu dojít.
↑ check_drummer:
What does a drowning number theorist say?
'log log log log ...'
Offline
#6 10. 03. 2018 17:00 — Editoval laszky (10. 03. 2018 17:00)
Re: Uspořádej čísla
↑ Andrejka3:
Pokud si vytvorime graf majici 305 vrcholu odpovidajicich cislum 1-305 a dva vrcholy budou spojene hranou, paklize je soucet odpovidajich cisel treti mocninou celeho cisla, potom se jedna o problem z teorie grafu - nalezeni Hamiltonovske cesty v grafu. Tzn. cesty, ktera projde po hranach grafu pres vsechny jeho vrcholy, pricemz kazdy navstivi prave jednou. Zkousel jsem to v programu wxmaxima, ale trva mu to hodne dlouho. Graf ma 305 vrcholu a 399 hran. Jeden jediny vrchol ma stupen 1, a to vrchol cislo 256, takze musi byt na kraji. Dalsich 173 vrcholu ma stupen 2, takze maji jiste sousedy.
Offline
#7 10. 03. 2018 17:05 — Editoval Andrejka3 (10. 03. 2018 17:07)
Re: Uspořádej čísla
What does a drowning number theorist say?
'log log log log ...'
Offline
#8 10. 03. 2018 17:29 — Editoval laszky (10. 03. 2018 17:30)
Re: Uspořádej čísla
↑ Andrejka3:
Problem si celkem zjednodusis, pokud si nejdriv najdes tech 173 cisel, ktere maji jasne sousedy. Jestlize problem spociva v nalezeni 304 "sousedstvi" (hran v grafu), potom minimalne 174 (pokud by vsechny byly za sebou) mas jasnych. Velmi pravdepodobne jich bude vic nez 174 - tipnul bych tak kolem 220-230. Takze ti zbyde uz jen vhodne vybrat dalsich 70-80 hran.
Offline
#9 10. 03. 2018 18:46
Re: Uspořádej čísla
↑ laszky:
No, teď mi zbývá 100 hra, pokud nemám někde chybu. Sousední vrcholy stupně dva jistě musí být propojeny hranou. Ale nevím, proč by vrchol stupně dva nemohl být konec Hamiltonovy cesty. Nemůže?
Díky za rady!
What does a drowning number theorist say?
'log log log log ...'
Offline
#10 10. 03. 2018 19:11
Re: Uspořádej čísla
↑ Andrejka3:
To asi muze byt... Jeste bych zkusil vyhledat tyhle situace.
Offline
#11 10. 03. 2018 23:09
Re: Uspořádej čísla
↑ laszky:
Tomu nerozumím. Čím je ta situace zajímavá?
Jako obvykle, když programuju, dělám spoustu chyb. Nový pokus: program by měl:
1) přidat hranu mezi vrcholem stupne 1 a sousedem
2) přidat hranu mezi dvema (sousednimi) vrcholy stupne 2
3) pridat hranu mezi vrcholem, ktery uz ma jednu pouzitou hranu, jednu zbyvajici a
a) sousednim vrcholem stupne 2
b) sousednim vrcholem stejne vlastnosti.
A vzdycky, kdyz uz mam vrchol se dvema pouzitymi hranami, tak ho odeberu a vytvorim si podgraf. Cestu si zapisuju zvlast.
Tak ted mi to pise, ze zbyva 223 hran do 304 cesty. Takže nic moc.
What does a drowning number theorist say?
'log log log log ...'
Offline
#12 10. 03. 2018 23:56
Re: Uspořádej čísla
Ja uz to zvladnul ;) Ale muj postup asi nebude vhodny, pokud by v grafu bylo mnohem vice hran...
Offline
#13 11. 03. 2018 00:11 — Editoval Andrejka3 (11. 03. 2018 00:15)
Re: Uspořádej čísla
↑ laszky:
Gratuluju! A zavidim :)
Znamena to, ze sis (sikovne) tipoval?
Edit: Na obrázku, jak jsou škrtnuté ty tři cesty. Proč by nemohla jedna z nich nebýt škrtnutá? Jednu neškrtnutou bychom škrtli a vytvořil by se jeden konec -- což je ok, ne?
What does a drowning number theorist say?
'log log log log ...'
Offline
#14 11. 03. 2018 00:33 — Editoval laszky (11. 03. 2018 00:34)
Re: Uspořádej čísla
↑ Andrejka3:
Pres ty hrany u vrcholu stupne 2 cesta vest musi, takze do toho vrcholu (napr. stupne 5 jako na obrazku) vedou urcite dve hrany z vrcholu stupne 2. Treti hrana z jednoho vrcholu vest nemuze, takze vsechny ostatni muzeme skrtnout ;-)
Offline
#16 11. 03. 2018 00:58
Re: Uspořádej čísla
↑ Andrejka3:
Nj, to je asi pravda... v tom pripade by mi to nefungovalo. Nicmene, vzhledem k tomu, ze se to behem tech 5 iteraci ani jednou nestalo, tak za tim asi bude nejake pravidlo, proc to fungovalo :-)
Offline
#17 11. 03. 2018 14:13
Re: Uspořádej čísla
↑ Andrejka3:
Napadlo me, ze pokud nejaky z vrcholu, ktery ma stupen 2 (cerveny vrchol na obrazku), bude nakonec koncovy, potom urcite lezi na nejake kruznici. Takze muzeme tu Hamiltonovskou cestu zvolit i jinak - tak aby tento vrchol koncovym nebyl (viz obrazek). Ale pravda je, ze ten muj postup selze, pokud nektera z tech hran, ktere odebiram, bude mostem - tj, pokud po odebrani te hrany vznikne nesouvisly graf. To bych tam mel nejak ohlidat.
Offline
#18 11. 03. 2018 14:28
Re: Uspořádej čísla
↑ laszky:
Popřemýšlím o tom. Určitě se k tomu ještě vrátím. 3 dny mi to nedalo spát. Přitom to je taková blbost.
Ještě bych ráda věděla, jestli to tvé řešení je stejné jako na webu ↑ Andrejka3:.
What does a drowning number theorist say?
'log log log log ...'
Offline
#19 11. 03. 2018 14:35
#20 11. 03. 2018 14:57
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Uspořádej čísla
Ahoj, já čekal nějaký elegantní důkaz, v tomto směru je škoda, že má úloha řešení. :-) Možná by bylo vhodné ji přesunout do "Algoritmy a programování". :-)
"Máte úhel beta." "No to nemám."
Offline
#21 11. 03. 2018 16:00 — Editoval laszky (11. 03. 2018 19:29)
Re: Uspořádej čísla
↑ Andrejka3:
Ahoj, ale zjistil jsem, ze je vice reseni... napr. pokud se podivas na konec toho reseni, na ktere jsi dala odkaz, potom lze namisto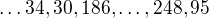
pouzit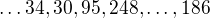 .
.
ale taky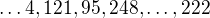 .
.
Offline
#22 11. 03. 2018 18:52
Re: Uspořádej čísla
↑ laszky:
Dobrý objev.
Vymyslela jsem vzory, které když se vyskytnou v grafu, řekne to, kterou hranou jít. Má to háček - v tom grafu nejsou :)
Ještě mě to baví, takže to nevzdávám.
↑ check_drummer:
Třeba se něco najde. Přesouvám...
What does a drowning number theorist say?
'log log log log ...'
Offline
#23 11. 03. 2018 22:28
Re: Uspořádej čísla
↑ check_drummer: Objevil jsem opravdu podivuhodný důkaz; bohužel tohle okénko na psaní příspěvků je příliš malé, aby se do něj vešel.
Offline
#24 13. 03. 2018 00:17
Re: Uspořádej čísla
↑ laszky:
Jasně. Hledal jsi všechny vrcholy takové, že když přidáš nějakou hranu do konstruované cesty a počítáš s vrcholem jako s koncem, jestli dostaneš těmi jednoduchými pravidly cestu délky 304.
Aspoň tak jsem to napsala v C.
Nebo jsi to dělal jinak?
Velké díky za trpělivost a že jsi všechny podrobnosti neprozradil! Díky tomu se můžu cítít, jako bych to vyřešila :D
What does a drowning number theorist say?
'log log log log ...'
Offline
#25 13. 03. 2018 17:22
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Uspořádej čísla
↑ Stýv:
Požádej admina, ať okénko zvětší. Máme více možností než za středověku. :-)
"Máte úhel beta." "No to nemám."
Offline

