Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 03. 2018 17:19 — Editoval laszky (13. 03. 2018 17:23)
2D lineární PDR druhého řádu
Dobry den,
narazil jsem na jednu PDR a podarilo se mi ji vyresit pouze pro  . Nenapada nekoho, jak to resit pro dalsi uhly
. Nenapada nekoho, jak to resit pro dalsi uhly  ? Budu rad, za kazdy tip.
? Budu rad, za kazdy tip.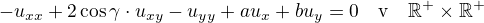
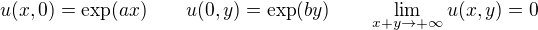
Pricemz konstanty 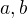 splnuji
splnuji  .
.
PS: Resil jsem to tak, ze jsem reseni hledal jako soucet/rozdil nekolika exponencialnich funkci tvaru 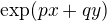
Offline
#3 18. 03. 2018 20:07
Re: 2D lineární PDR druhého řádu
↑ MichalAld:
Pro 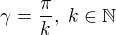 vychazeji p a q v exponentu tech funkci
vychazeji p a q v exponentu tech funkci 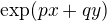 zaporne. Pro jine racionalni nasobky
zaporne. Pro jine racionalni nasobky  vyjde vzdy aspon jedno p nebo q kladne, takze neni splnena okrajova podminka
vyjde vzdy aspon jedno p nebo q kladne, takze neni splnena okrajova podminka 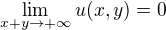 .
.
Offline
