Matematické Fórum

Peter_CSR · 26. 03. 2018 12:58

Ahoj,

"Nech p je nepárne prvočíslo. Najväčší spoločný deliteľ všetkých čísel 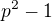$p^{2} - 1$
sa rovná:"

nechápem prečo píšu o prvočísle že je nepárne... Najväčšie známe prvočíslo má cca 23 249 425 číslic. To idem skúšať jedno po druhom, umocňovať, odčítať jednotku a deliť...

Správna odpoveď by mala byť 8. Viem len že by som vzťah (asi) upravil na (p+1)*(p-1), kde každá zátvorka bude deliteľná dvoma...a ich súčin musí byť deliteľný 4.... a teraz čo?

zdenek1 · 26. 03. 2018 13:02

↑ Peter_CSR:
jsou to dvě sudá za sebou jdoucí čísla. Jedno z nich je jistě dělitelné čtyřmi a druhé ne.

vanok · 26. 03. 2018 13:02

Ahoj ↑ Peter_CSR: ,
p-1, p+1 su dve po sebe iduce parne cisla.
Co z toho mozes vyvodit?

Peter_CSR · 26. 03. 2018 13:13

takže, jedno je deliteľné 4, tj, dá sa napísať ako 4*p, druhé 2, čiže zapíšem ako 2*q, takže (p + 1)(p - 1) = 8pq.

Otázka ostáva, či je to úplná množina riešení... ale nemám asi spôsob, ako o tom určiť čokoľvek ďalšie, alebo mám?

vanok · 26. 03. 2018 14:12

↑ Peter_CSR:,
To prve nepis ako 4p ale napr. 4m. Vsak p si uz pouzil.

Poznamka. Neparne prvocislo p pisu lebo jedinne parne prvocislo je 2. A to vtedy neplati.

Staci?

vlado_bb

↑ Peter_CSR: Ako myslis svoju otazku, ci je mnozina rieseni uplna? Mal si najst najvacsi spolocny delitel, teda JEDNO cislo. Nasiel si ho. Co by podla teba mala byt ta “uplna mnozina rieseni”?

A potom, tvoja poznamka o najvacsom znamom prvocisle napoveda, ze si asi ulohu nepochopil spravne. V ulohe sa chce najst najvacsi spolocny delitel VSETKYCH cisel s uvedenou vlastnostou a nie vsetkych takych, ze $p$ je zname. Cize ak by si aj (odhliadnuc od casovej narocnosti) vyskusal vsetky zname prvocisla, ulohu by si nevyriesil.

laszky · 26. 03. 2018 14:46

↑ vlado_bb:

Mne ta uloha prisla taky trochu divne formulovana a pochopil jsem ji az z tve interpretace... Spravne by to spis melo byt: "Uvazujme mnozinu $\{p_1,p_2,p_3,\dots\}$ vsech lichych (neparnych) prvocisel. Jaky je nejvetsi spolecny delitel cisel $p_1^2-1, p_2^2-1, p_3^2-1, \dots$ ?" Nebo nejak podobne, ne? :-)

vlado_bb

↑ laszky: Ano, tiez som si to takto preformuloval.

DominikBnP · 26. 03. 2018 14:51

To, že každé takové číslo tvaru $p^2-1$ bude dělitelné osmi, jste odvodili společně správně, ale ještě musíš ukázat, že největší společný dělitel nebude větší než 8, tedy nějaký násobek osmi. Ale to je hned vidět z toho, že pro p=3 je $p^2-1$ rovno právě osmi, tedy největší společný dělitel všech těchto čísel i s tou osmičkou nemůže být větší, než nejmenší z nich, tedy 8.

vlado_bb · 26. 03. 2018 14:56

↑ DominikBnP: Podla coho usudzujes, ze ↑ Peter_CSR: ma problem prave s touto uvahou a ze ju nezvladne sam?

DominikBnP · 26. 03. 2018 15:01

↑ vlado_bb:
Proč si myslíš, že je tento tvůj dotaz na mě k věci, tedy nikoli OT?

vlado_bb · 26. 03. 2018 15:02

↑ DominikBnP: Pretoze sa tyka tohoto vlakna, ktoreho cielom nie je ulohu vyriesit, ale pomoct zadavatelovi, aby ju vyriesil.

DominikBnP · 26. 03. 2018 15:12

↑ vlado_bb:

Aha, až na to, že tady padl neúplný postup, správně sice podaný, vydávaný ale za kompletní. A nedotažený důkaz není korektní. Pro některé z těch prvočísel to navíc i vyjde víc, třeba pro 11 a 19 apod.

vlado_bb · 26. 03. 2018 15:13

↑ DominikBnP: Ano, ale preco myslis, ze zadavatel ma prave s tymto problem a ze ho nezvladne sam?

Peter_CSR · 26. 03. 2018 15:16

DominikBnP napsal(a):
To, že každé takové číslo tvaru $p^2-1$ bude dělitelné osmi, jste odvodili společně správně, ale ještě musíš ukázat, že největší společný dělitel nebude větší než 8, tedy nějaký násobek osmi. Ale to je hned vidět z toho, že pro p=3 je $p^2-1$ rovno právě osmi, tedy největší společný dělitel všech těchto čísel i s tou osmičkou nemůže být větší, než nejmenší z nich, tedy 8.

áno, skutočne, toto je vec, ktorá mi unikala.

A Vlado_bb mal pravdu, zadaniu úlohy som neporozumel správne. To, že úlohe vyhovuje 8, takže žiadne číslo väčšie než 8 by už nemohlo byť riešením.

DominikBnP · 26. 03. 2018 15:17

↑ vlado_bb:

Já to nebudu zkoumat. Prostě tady padl postup, který nebyl kompletní, a pokud by se s tím takto spokojil, nebude to mít celé a tedy ani dobře. A i kdybych to autistické pravidlo o tom, že se tady příklad nesmí vyřešit, bral jako normu, tak tady došlo ke zmatení, protože nikdo nedal tu informaci, že to není všechno, působilo to z textu, jako že to všechno už je, a tedy došlo k vytvoření pěkné pasti.

vlado_bb · 26. 03. 2018 15:18

↑ Peter_CSR: Jasne, najvacsi spolocny delitel mnoziny cisel je nanajvys minimum z tejto mnoziny, spravne.

vlado_bb · 26. 03. 2018 15:20

↑ DominikBnP: Nestacilo sa zadavatela opytat, ci to uz povazuje za uplne riesenie? A k tomu autistickemu pravidlu ... ak povazujem pravidlo o tom, ze futbal sa nehra rukou, za autisticke, je to moje plne pravo, ale v tom pripade sa nebudem uchadzat o clenstvo vo futbalovom klube.

DominikBnP · 26. 03. 2018 15:22

↑ vlado_bb:
Já třeba považuju za autistické například přijet k dopravní nehodě, vidět člověka v autě, který neví, jak ven, a otevřít mu dveře a pak se ho ptát, jestli to už je dobré.

Peter_CSR · 26. 03. 2018 15:24

DominikBnP napsal(a):
↑ vlado_bb:
Já třeba považuju za autistické například přijet k dopravní nehodě, vidět člověka v autě, který neví, jak ven, a otevřít mu dveře a pak se ho ptát, jestli to už je dobré.

:D :D :D

Tento vtip mi príde vtipnejší než by mal, a nie len koli vladovi_bb :D :D :D

Nikdy nerobte z matematika záchrankára. Overí, či situácia má riešenie a spokojne odkráča :D

vlado_bb · 26. 03. 2018 15:24

↑ DominikBnP: Ano, vsetko ma svoje pravidla. O spravani sa pri dopravnej nehode hovoria zakonne a eticke normy. O spravani sa tu na fore zasa jeho zvyklosti a pravidla.

DominikBnP · 26. 03. 2018 15:25

↑ Peter_CSR:
No a právě proto jsem tě na to upozornil, že to, že je to 8, ještě musíš obhájit i shora, nejen zdola. Bylo to neintuitivní v momentě, kdy s těmito příklady nemáš takovou zkušenost.

DominikBnP · 26. 03. 2018 15:28

↑ vlado_bb:

A tady je právě příklad toho, proč je kvůli tomu toto fórum zrádné a jak takto může dát špatnou radu. Kdo totiž dostane nekompletní postup, který ale považuje za kompletní, je na tom hůř, než ten, kdo žádný postup nedostal.

A proto tady opravdu nehledat učitele matematiky.

Peter_CSR · 26. 03. 2018 15:42

DominikBnP napsal(a):
↑ Peter_CSR:
No a právě proto jsem tě na to upozornil, že to, že je to 8, ještě musíš obhájit i shora, nejen zdola. Bylo to neintuitivní v momentě, kdy s těmito příklady nemáš takovou zkušenost.

ah, som dnes strašne nesústredený.

jediná schodná cesta ktorú vidím je prepísanie výrazu na súčin a určenie jeho vlastností...

...mylím...neviem...

sorry, zle mi to dnes myslí.

vlado_bb · 26. 03. 2018 16:13

↑ Peter_CSR: Prosim ta, odpovedz jasne a strucne na tieto otazky:

1. Vsimol si si, ze uloha je uz vyriesena?

2. V com este vidis problem?

Matematické Fórum

#1 26. 03. 2018 12:58

Najväčší spoločný deliteľ

#2 26. 03. 2018 13:02

Re: Najväčší spoločný deliteľ

#3 26. 03. 2018 13:02

Re: Najväčší spoločný deliteľ

#4 26. 03. 2018 13:13

Re: Najväčší spoločný deliteľ

#5 26. 03. 2018 14:12

Re: Najväčší spoločný deliteľ

#6 26. 03. 2018 14:36 — Editoval vlado_bb (26. 03. 2018 14:41)

Re: Najväčší spoločný deliteľ

#7 26. 03. 2018 14:46

Re: Najväčší spoločný deliteľ

#8 26. 03. 2018 14:47 — Editoval vlado_bb (26. 03. 2018 14:47)

Re: Najväčší spoločný deliteľ

#9 26. 03. 2018 14:51

Re: Najväčší spoločný deliteľ

#10 26. 03. 2018 14:56

Re: Najväčší spoločný deliteľ

#11 26. 03. 2018 15:01

Re: Najväčší spoločný deliteľ

#12 26. 03. 2018 15:02

Re: Najväčší spoločný deliteľ

#13 26. 03. 2018 15:12

Re: Najväčší spoločný deliteľ

#14 26. 03. 2018 15:13

Re: Najväčší spoločný deliteľ

#15 26. 03. 2018 15:16

Re: Najväčší spoločný deliteľ

DominikBnP napsal(a):

#16 26. 03. 2018 15:17

Re: Najväčší spoločný deliteľ

#17 26. 03. 2018 15:18

Re: Najväčší spoločný deliteľ

#18 26. 03. 2018 15:20

Re: Najväčší spoločný deliteľ

#19 26. 03. 2018 15:22

Re: Najväčší spoločný deliteľ

#20 26. 03. 2018 15:24

Re: Najväčší spoločný deliteľ

DominikBnP napsal(a):

#21 26. 03. 2018 15:24

Re: Najväčší spoločný deliteľ

#22 26. 03. 2018 15:25

Re: Najväčší spoločný deliteľ

#23 26. 03. 2018 15:28

Re: Najväčší spoločný deliteľ

#24 26. 03. 2018 15:42

Re: Najväčší spoločný deliteľ

DominikBnP napsal(a):

#25 26. 03. 2018 16:13

Re: Najväčší spoločný deliteľ

Zápatí