Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 03. 2018 13:22
Sústava nerovníc
Ahoj,
toto je veľmi ľahká otázka, ale nie je mi celkom jasné, ako sa to obecne rieši...
https://imgur.com/a/LSeO7
Mohol by som si z toho spraviť lin rovnice a vypočítať bázové vektory, ale neviem na čo by mi to bolo... aldebo by som sa mohol zamyslieť nad každou nerovnosťou a čo znamená... strašne zdĺhavé...
Nejaká rýchla a spoľahlivá metóda?
Ďakujem.
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
- (téma jako vyřešené označil(a) Peter_CSR)
#3 26. 03. 2018 13:45 — Editoval Peter_CSR (26. 03. 2018 13:47)
Re: Sústava nerovníc
y > x - 1
a
y < x + 2
...no... z toho vidím, že ak x = 0, y patrí (-1,2)
y + 1 > x
a
y - 2 < x
ak y = 0, x patrí (-2, 1).
Ďalší krokom by bolo nakreslenie si štyroch bodov pre okrajové podmienky x = 0 a y = -1 alebo 2, y = 0 a x = -2 alebo 1.
a na záver, otestujem či množina riešení ide napr. pre x idúce do plus nekonečna na y idúce do plus alebo mínus nekonečna.... podľa toho spojím 4 body, ako mi vznikli... myslím... týmto posledným krokom som si nie úplne istý...
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#5 26. 03. 2018 14:05
Re: Sústava nerovníc
nie som si istý... V tomto prípade, mám 4 body, ktoré chcem spojiť 2 priamkami, a to možem spraviť dvojako. Obe prípady majú bodu nad i pod priamkou....
nie som si istý, čo sa ty myslí...
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#6 26. 03. 2018 15:11
Re: Sústava nerovníc
↑ Peter_CSR: Obe nerovnosti maju byt splnene sucasne, to je vyznam slova “obe” v texte ulohy. Teda najdeme mnozinu bodov, ktore vyhovuju prvej z nich, potom druhej (toto predpokladam vies) a potom uvazime, ze nas zaujimaju body, ktore patria do oboch najdenych mnozin. Moze byt?
Offline
#7 26. 03. 2018 17:27
Re: Sústava nerovníc
Zdravím vespolek, nehledej v tom zbytečně složitosti. Načrtneš si přímku y=x-1. Pak si zvolíš libovolný bod, neležící na této přímce a dosadíš si ho do dané nerovnosti y>x-1. Pokud bude nerovnost splněna, tato polorovina bude řešením, pokud ne, řešením bude ta opačná. Stejným způsobem vyřešíš i druhou nerovnost (přímka, dosazení bodu, určení té správné poloroviny). Výsledkem, jak už ti naznačuje vlado, bude průnik obou polorovin, neboť to, co v logice znamená 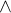 , v množinových operacích značí
, v množinových operacích značí 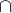 .
.
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#8 26. 03. 2018 17:50
Re: Sústava nerovníc
Peter_CSR napsal(a):
... aldebo by som sa mohol zamyslieť nad každou nerovnosťou a čo znamená... strašne zdĺhavé...
Jenže asi přesně tohle autor příkladu zamýšlel - aby se nad tím člověk ZAMYSLEL, protože na tom nic k počítání vlastně není.
Offline
#9 26. 03. 2018 20:09
Re: Sústava nerovníc
↑ MichalAld:
myslenie ma bolí :D Ja radšej počítam :D
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#10 26. 03. 2018 21:53
Re: Sústava nerovníc
↑ Peter_CSR: Teraz budem parafrazovat jedneho kolegu z fora - pokojne pocitaj aj bez rozmyslania, len tomu prosim nehovor matematika.
Offline
#11 26. 03. 2018 22:13
Re: Sústava nerovníc
↑ vlado_bb:
ako znel pôvodný výrok? :)
Inak, myslím źe to bol MichalAld, čo vynašiel princíp "keď nevieš, predel nulou"... :) Len taká perlička, čo ma pobavila... :)
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#12 26. 03. 2018 22:20
Re: Sústava nerovníc
↑ Peter_CSR: Klidně si to sbírejte, když vám to chutná, ale neříkejte tomu proboha václavky. (check_drummer)
Offline
#13 26. 03. 2018 22:40
Offline