Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 04. 2018 21:31
Derivace a limita funkce s absolutní hodnotou
Ahoj,
mohu poprosit o pomoc? Potřebuji zderivovat tuto funkci a dokázat, že limita v bodě -1 je nekonečno.
f: y = 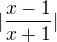
Ta derivace mě napadá leda přes intervaly, tedy (-∞;-1), (-1;1) a (1;∞). Ovšem jak pak dokázat monotónnost v jiných intervalech a dokázat, že existují/neexistují body, kde derivace neexistuje, to už netuším.
Díky moc!
Offline
#3 01. 04. 2018 21:58
Re: Derivace a limita funkce s absolutní hodnotou
↑ laszky:
Haha, díky moc za snahu, každopádně tenhle postup jsem si našel na tomto fóru ještě předtím, než jsem toto téma založil, ale absolutně nevím, jak s tím pracovat - pochopil jsem jen, že signum přiřazuje patřičné znaménko, ale jak s tím pracovat při derivaci a následném hledání například druhé derivace, podezřelých bodů z extrémů atd., to je zatím nad moje středoškolské znalosti :(
Ale děkuji za snahu, jdu o tom něco hledat, alespoň překvapit učitele :)
Offline
#6 01. 04. 2018 22:19
Re: Derivace a limita funkce s absolutní hodnotou
↑ vlado_bb:
Dle tužkou dopsané poznámky v tabulkách  , důkaz podle internetu přes tzv. chain rule. Trošku jsem si ho prošel, každopádně v angličtině, tak snad jsem to jakžtakž pochopil.
, důkaz podle internetu přes tzv. chain rule. Trošku jsem si ho prošel, každopádně v angličtině, tak snad jsem to jakžtakž pochopil.
Offline
#8 01. 04. 2018 22:25
Re: Derivace a limita funkce s absolutní hodnotou
↑ Dáda78: Pokial ma ist o odpoved na moju otazku, nepotrebujes nijaky dokaz, nijake chain rule, nijaky internet. Staci pochopit co je to derivacia. Bez toho ziadne dalsie aktivity v tomto smere nemaju zmysel.
Offline
#9 01. 04. 2018 22:31
Re: Derivace a limita funkce s absolutní hodnotou
↑ vlado_bb:
promiň, já už si poslední dobou najel na takový pravidlo, že si vše v matematice snažím dokazovat :-)
tak základní derivace si myslím, že ovládám, akorát jsem se ztratil, když jsem narazil na příklad s absolutní hodnotou, to jsem si dokázal vyřešit jen přes ty intervaly, ale očekávám nějaký celistvější výsledek :-)
Offline
#11 01. 04. 2018 22:39
Re: Derivace a limita funkce s absolutní hodnotou
ak smiem poradiť tiež, odpoveď na vladovu otázku je strašne jednoduchá, zamysli sa len čo presne derivácia znamená, aké sú podnienky jej existencie a máš to. Úplne rovnaký postup uplatníš aj na svojom príklade.
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#12 01. 04. 2018 22:48
Re: Derivace a limita funkce s absolutní hodnotou
↑ Peter_CSR:
tak derivace je směrnice tečny dané funkce a její podmínkou je spojitost této funkce?
Offline
#14 01. 04. 2018 22:50
Re: Derivace a limita funkce s absolutní hodnotou
↑ Dáda78: skoro správne, ale tie podmienky sú tam dve. Spomeň si na ňu a potom vyrieš vladov príklad. Uvažuj, ako by sa derivácia graficky chovala, ako by si na tú funkciu prikladala dotyčnicu.
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#15 01. 04. 2018 22:52
Re: Derivace a limita funkce s absolutní hodnotou
Dáda78 napsal(a):
↑ Peter_CSR:
tak derivace je směrnice tečny dané funkce a její podmínkou je spojitost této funkce?
alebo zober definíciu derivácia vyjadrenú prostredníctvom limity funkcie a vypočítaj ju tak pre každý bod. Algebraicky náročnejšie ale ekvivalentné.
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#17 01. 04. 2018 23:00
Re: Derivace a limita funkce s absolutní hodnotou
presne ako píšeš. a ako lazsky naznačil, je tu ešte podmienka nejak súvisiaca so spojitosťou.
tečna je dotyčnica :)
keď si to vieš graficky predstaviť, skús sa rovnakým štýlom zamyslieť čo symbolizuje tvoja úloha...
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#20 01. 04. 2018 23:11
Re: Derivace a limita funkce s absolutní hodnotou
laszky napsal(a):
↑ Dáda78:
Ja jen, zes rikal, ze podminkou je spojitost funkce... takze spojitost je trochu malo :-) Dokonce jsou i funkce, ktere jsou spojite, ale nemaji derivaci v zadnem bode ;-)
ktorá funkcia je spojitá ale nemá deriváciu v žiadnom bode?
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#21 01. 04. 2018 23:17
Re: Derivace a limita funkce s absolutní hodnotou
↑ Peter_CSR:
Napriklad Weierstrassova funkce.
Offline
#22 01. 04. 2018 23:33
Re: Derivace a limita funkce s absolutní hodnotou
laszky napsal(a):
↑ Peter_CSR:
Napriklad Weierstrassova funkce.
fíha!
toto je troška OT, ale neporadil by si mi ako postupovať, keď chcem nájsť funkciu ktorá je definovaná na celom R ale spojitá práve v jedinom bode? Viem že by som chcel nejak upravovať Dirichletovu fumkciu, napríklad, ale nie som si istý celkom ako... nehľadám odpoveď, iba poštuchnutie!
Inak, ak by ťa bavila kombinátorika, postol som 2 otázky a nejak v nich tápam... :)
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#23 01. 04. 2018 23:46
Re: Derivace a limita funkce s absolutní hodnotou
↑ Peter_CSR:
Staci kdyz tu Dirichletovu funkci D(x) prenasobis iksem... vysledek je spojity v nule ;-) ...promin, moc na tu kombinatoriku nemam naladu :D
Offline
#24 01. 04. 2018 23:53
Re: Derivace a limita funkce s absolutní hodnotou
no, tak si mi to prezdradil, tešil som sa že na vec prídem sám, ale dík :)
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#25 01. 04. 2018 23:56
Re: Derivace a limita funkce s absolutní hodnotou
↑ Peter_CSR:
Aha prepac... myslel jsem, ze sis do me stouchl (postuchnutie) a tys to myslel jinak :D Ale tak stale si muzes tu spojitost v nule zkusit dokazat ;-)
Offline

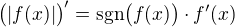 vsude mimo body, kde
vsude mimo body, kde 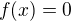 .
.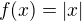 ?
?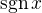 je nula vsude mimo
je nula vsude mimo  , kde derivace neexistuje. A pokud ti vadi signum, pak ho staci zapsat jako
, kde derivace neexistuje. A pokud ti vadi signum, pak ho staci zapsat jako 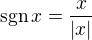 (opet plati vsude mimo x=0).
(opet plati vsude mimo x=0).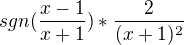 ?
? je spojita funkce, presto nema v 0 derivaci ;-)
je spojita funkce, presto nema v 0 derivaci ;-)