Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 04. 2018 13:52 — Editoval liamlim (03. 04. 2018 21:16)
Další "důkaz" Velké Fermatovy věty :D
edit2: Fakt se mi to nechce podrobně přepisovat. Napíšu sem jednotlivé věty a prosím o reakci, která část vypadá podezřele. Tu pak případně rozepíši více.
.....................................................................................
Fermatova věta: Neexistují po dvou nesoudělná  ,
,  a
a  tak, že pro nějaké prvočíselné
tak, že pro nějaké prvočíselné 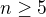 platilo
platilo 
.....................................................................................
1) Snadno se ukáže, že 
2) Definujeme 
3) Snadno se ukáže, že 
4) Snadno se ukáže, že je  liché
liché
5) Snadno se ukáže, že je  nesoudělné s
nesoudělné s 
6) Snadno se ukáže, že 
7.a) Nechť  je dělitelné
je dělitelné  . Pak
. Pak  .
.
7.b) Nechť  není dělitelné
není dělitelné  . Pak
. Pak  dělí
dělí 
.......................................................................................
**Doteď to byly triviality. V předchozích bodech určitě chyba není.**
8) Díky A se celkem snadno ukáže, že libovolné dělitele  , které nejsou ani
, které nejsou ani  ani tvaru
ani tvaru  dělí současně
dělí současně 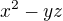 ,
, 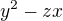 a
a  .
.
9) Ukáže se, že  má alespoň dva různé prvočíselné dělitele tvaru
má alespoň dva různé prvočíselné dělitele tvaru 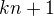
10) S pomocí 7 se celkem snadno ukáže, že libovolný dělitel  , který je tvaru
, který je tvaru  , je tvaru
, je tvaru 
11) Existují tedy prvočísla  ,
,  tak, že
tak, že  i
i  jsou tvaru
jsou tvaru  a současně
a současně 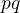 dělí
dělí  .
.
12) Ukáže se, že 
13) Ukáže se, že  nedělí
nedělí  , což je spor s tím, že
, což je spor s tím, že  a
a  jsou prvočísla tvaru
jsou prvočísla tvaru  .
.
...................................................................................
Užitečná tvrzení, která se dají buď najít na netu, nebo snadno dokázat:
A) Pro každá nesoudělná  ,
,  a prvočíselné
a prvočíselné  platí:
platí:
A1)  nedělí
nedělí 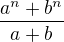
A2) Všechny dělitele 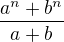 jsou buď
jsou buď  nebo tvaru
nebo tvaru  .
.
A3)  dělí
dělí 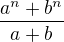 právě tehdy, když
právě tehdy, když  dělí
dělí 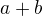
Offline
#2 03. 04. 2018 21:41
Re: Další "důkaz" Velké Fermatovy věty :D
Rozhodl jsem se ukázat samotný konec mého "důkazu" od části (11). Předpokládejme tedy, že máme tvrzení (11) dokázané a ukažme si spor...
Nejprve dokažme tvrzení (12):
Dle (7a) platí  . Díky (5) a eulerově větě dostaneme
. Díky (5) a eulerově větě dostaneme  . Díky faktu, že
. Díky faktu, že  ,
,  jsou prvočísla tvaru
jsou prvočísla tvaru  můžeme kongruenci pokrátit, čímž dostaneme přímo tvrzení (12).
můžeme kongruenci pokrátit, čímž dostaneme přímo tvrzení (12).
Důkaz tvrzení (13) už vlastně znamená samotný spor s existencí  ,
,  , tedy dokončení důkazu celé Velké Fermatovy věty. Proto důkaz rozepíši podrobněji. Nejprve z tvrzení (12) můžeme odvodit následující kongruence (všechny jsou modulo
, tedy dokončení důkazu celé Velké Fermatovy věty. Proto důkaz rozepíši podrobněji. Nejprve z tvrzení (12) můžeme odvodit následující kongruence (všechny jsou modulo 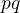 ):
):
Část X0:


Po sečtení dostaneme:
neboli
Část X1:
Stejně tak ze (12) přímo odvodíme kongruence (též jsou všechny modulo 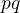 ):
):


Jejich sečtením dostaneme 
Což díky (12) je to samé jako 
neboli
..........................
Spojením části X0 a X1 přímo dostaneme následující:

Buď 3 nedělí  a jsme hotovi nebo 3 dělí
a jsme hotovi nebo 3 dělí  a tedy můžeme kongruenci vykrátit na tvar:
a tedy můžeme kongruenci vykrátit na tvar:
EDIT: tady si to rozmyslím. možná jsem už narazil na chybu. jak se to snažím přepisovat opravdu podrobně, tak jde některé věci lépe vidět
Offline
