Matematické Fórum

kaja(z_hajovny) · 19. 05. 2009 20:42

Preji pekny den,

nenapada prosim nekoho, kdo treba zrovna cerstve prosel kurzem numerickych metod, jak co nejsikovneji prevest na schodovity tvar matici, ktera ma cca 60 tisic radku a sloupcu? Nakonec by z toho mel byt program ve Fortranu.

Diky za jakekoliv odkazy, kdyz se to bralo ve skole tak jsem asi byl nemocny :)

jendula11 · 19. 05. 2009 20:45

↑ kaja(z_hajovny):
no matlab by to určitě zvládnul pokud by to stačílo?

kaja(z_hajovny) · 19. 05. 2009 20:49

↑ jendula11:
Mate s tak velkyma maticema nekdo zkusenosti? Matice neni nijak ridka ani pasova ani nic takoveho. Jak je to s casem vypoctu a s presnosti? (budou to data z nejakeho druzicoveho mereni)

jendula11 · 19. 05. 2009 20:58

↑ kaja(z_hajovny):
No zkušenosti, největší matice se kterou jsem pracoval v matlabu byla 30*30 ale myslím že by to mělo běžet, tedy nevím proč byto nemělo jít

musixx · 20. 05. 2009 11:14

jendula11 napsal(a):
↑ kaja(z_hajovny):
no matlab by to určitě zvládnul pokud by to stačílo?

Tak tohle mi prijde hodne naivni.

Min naivni a mozna preci jen realistictejisi nez jendula11 mi prijde tato uvaha.

Dostat nuly do j-teho sloupce tak, ze v nem vyberu prvek blizky medianu ci prumeru a pomoci toho radku "odstranovat" - tim se alespon pravdepodobne vyhnu castemu deleni malych cisel a podobnym problematickym operacim. Najit prumer je linearni cas, se znalosti prumeru najit neco jemu blizke je opet lienarni cas vuci radu matice. Pricist k-nasobek jednoho radku k l-nasobku jineho radku je 3*rad_matice=3r float-operaci.

Celkem tedy [2r + (r-1) * 3r] flop a mam nuly v jednom sloupci. Na malych maticich nezalezi, takze uvazme treba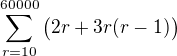
$\sum_{r=10}^{60000}\big(2r+3r(r-1)\big)$ ,
coz je pri predpokladu 500 Mflops (vicemene jedno dnesni standardni PC) cca 120 hodin vypocetniho casu.

Operace na jednom prvku matice je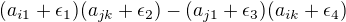
$(a_{i1}+\epsilon_1)(a_{jk}+\epsilon_2)-(a_{j1}+\epsilon_3)(a_{ik}+\epsilon_4)$ ,
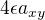coz se od hledaneho $a_{i1}a_{jk}-a_{j1}a_{ik}$ lisi o $4\epsilon a_{xy}$ . Nemohu tedy rict vice nez se relativni chyba se jednim krokem zvysi ctyrikrat.

Takovychto operaci delam s prvkem matice az 60000, tedy jsem nekde na max. sesti radech v decimalnim zapise, ktere ztracim v presnosti. Pri uziti IEEE 754 64bit float cisla mam vysledek s predpokladanou presnosti 1e-9 pro kazdy prvek matice. Na vstupu je kazdy prvek matice s presnosti 2.22e-16.

Matematické Fórum

#1 19. 05. 2009 20:42

prevod na schodovity tvar - obrovska matice

#2 19. 05. 2009 20:45

Re: prevod na schodovity tvar - obrovska matice

#3 19. 05. 2009 20:49

Re: prevod na schodovity tvar - obrovska matice

#4 19. 05. 2009 20:58

Re: prevod na schodovity tvar - obrovska matice

#5 20. 05. 2009 11:14

Re: prevod na schodovity tvar - obrovska matice

jendula11 napsal(a):

Zápatí