Matematické Fórum

Aldis · 06. 01. 2014 18:51

Ahoj všichni, moc prosím o pomoc s příkladem. Nechápu ani základ a tento potřebuji mít do zítra hotový. Zadání: Napište rovnici elipsy, která má osy shodné s osami soustavy souřadnic a prochází body M(-6,√7), N(3√2,4).

Arabela

Ahoj ↑ Aldis:,
ak má mať elipsa hlavnú os v osi x a vedľajšiu v osi y, jej rovnica je
$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ .
Súradnice daných bodov musia vyhovieť tej rovnici... Ďalej budeš vedieť?

Aldis · 06. 01. 2014 19:09

↑ Arabela:Děkuju. Obávám se, že dělám někde chybu. Vzorec mi je jasný, ale potom s tím asi pracuji špatně.

Arabela

↑ Aldis:
prepáč, tamto bola rovnica hyperboly. Má to byť so znamienkom plus.

Arabela · 06. 01. 2014 20:04

↑ Aldis:
$\frac{(-6)^{2}}{a^{2}}+\frac{(\sqrt{7})^{2}}{b^{2}}=1$
$\frac{(3\sqrt{2})^{2}}{a^{2}}+\frac{4^{2}}{b^{2}}=1$

Aldis · 06. 01. 2014 20:50

stále mi to nechce vyjí. Prosím, šlo by trochu ↑ Arabela:více rozepsat kroky?

Peterslovak · 06. 01. 2014 20:55

Za $a^{2}$ dosad 50
Za $b^{2}$ dosad 25
Ve vzorci u Arabely

Arabela · 07. 01. 2014 14:51

↑ Aldis:
$\frac{36}{a^{2}}+\frac{7}{b^{2}}=1$
$\frac{18}{a^{2}}+\frac{16}{b^{2}}=1$
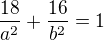
Po prenásobení menovateľmi
$36b^{2}+7a^{2}=a^{2}b^{2}$
$18b^{2}+16a^{2}=a^{2}b^{2}$
Dáme do rovnosti výrazy a^2.b^2, dostávame
$36b^{2}+7a^{2}=18b^{2}+16a^{2}$
$18b^{2}=9a^{2}$
$2b^{2}=a^{2}$
Dosadením za a^2 do jednej z dvoch rovníc v úvode môjho príspevku dostávame napríklad
$36b^{2}+7.2b^{2}=2b^{2}.b^{2}$
a po vydelení oboch strán rovnice výrazom b^2
$36+14=2b^2$
$2b^2=50$
$b^2=25$
$b=5$
Dosadením do výrazu
$a^{2}=2b^{2}$
dostaneme
$a^{2}=50$ , resp.
$a=5\sqrt{2}$

Cheop · 07. 01. 2014 14:55 — Editoval Cheop (07. 01. 2014 15:02)

↑ Arabela:
Zdravím, jen taková technická:
Pokud druhou rovnici vynásobím (-2) a sečtu s první rovnící dostanu hned:
$b^2=25$ a pak už lehce dopočítám
$a^2=50$ třeba z druhé rovnice a mám hotovo

Arabela · 07. 01. 2014 15:28

Zdravím ↑ Cheop:,
áno, vďaka, Vaše riešenie je samozrejme elegantnejšie. Ja som sa snažila byť hodne "polopatistická"...:)... Ale keď si to kolegyňa Aldis všetko prejde, aj s doplňujúcimi poznámkami, mala by v tom mať jasno (aspoň tomu chcem veriť)...

Aldis · 07. 01. 2014 15:57

↑ Arabela:Děkuji mnohokrát za oba způsoby řešení. Příklad odevzdán i se slovním vysvětlením:))

Arabela · 07. 01. 2014 18:42

↑ Aldis:
rada som pomohla...:)

JJohn · 15. 04. 2018 12:02

↑ Arabela:
Ahoj,

jak se zjistí, že hlavní osa je shodná s osou x a ne s osou y?

misaH · 15. 04. 2018 12:11 — Editoval misaH (15. 04. 2018 12:18)

↑ JJohn:

:-D

To sa pýtaš dobre, po viac než 4 rokoch...

Pod ktorým písmenkom v rovnici elipsy je väčšie číslo, s tou osou je rovnobežná hlavná os.

Aspoň myslím, že myslím dobre... :-)

JJohn · 15. 04. 2018 14:14

↑ misaH:
V zadání nemáš danou rovnici, potřebuješ nejdřív zjistit, ve kterém jmenovateli je a a ve kterém b.

zdenek1 · 15. 04. 2018 14:46

↑ JJohn:
Nepotřebuješ. $a$ a $b$ jsou na počátku jen písmenka. Teprve když vypočítáš jejich číselné hodnoty poznáš, které označuje hlavní (to větší) a které vedlejší poloosu.

JJohn · 15. 04. 2018 15:49

↑ zdenek1:
Děkuji.

Matematické Fórum

#1 06. 01. 2014 18:51

Kuželosečky - elipsa

#2 06. 01. 2014 19:04 — Editoval Arabela (06. 01. 2014 20:05)

Re: Kuželosečky - elipsa

#3 06. 01. 2014 19:09

Re: Kuželosečky - elipsa

#4 06. 01. 2014 19:57 — Editoval Arabela (06. 01. 2014 20:04)

Re: Kuželosečky - elipsa

#5 06. 01. 2014 20:04

Re: Kuželosečky - elipsa

#6 06. 01. 2014 20:50

Re: Kuželosečky - elipsa

#7 06. 01. 2014 20:55

Re: Kuželosečky - elipsa

#8 07. 01. 2014 14:51

Re: Kuželosečky - elipsa

#9 07. 01. 2014 14:55 — Editoval Cheop (07. 01. 2014 15:02)

Re: Kuželosečky - elipsa

#10 07. 01. 2014 15:28

Re: Kuželosečky - elipsa

#11 07. 01. 2014 15:57

Re: Kuželosečky - elipsa

#12 07. 01. 2014 18:42

Re: Kuželosečky - elipsa

#13 15. 04. 2018 12:02

Re: Kuželosečky - elipsa

#14 15. 04. 2018 12:11 — Editoval misaH (15. 04. 2018 12:18)

Re: Kuželosečky - elipsa

#15 15. 04. 2018 14:14

Re: Kuželosečky - elipsa

#16 15. 04. 2018 14:46

Re: Kuželosečky - elipsa

#17 15. 04. 2018 15:49

Re: Kuželosečky - elipsa

Zápatí