Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 04. 2018 13:05
- Adélka Hrubá
- Zelenáč
- Příspěvky: 8
- Škola: SVSE Praha
- Pozice: Student
- Reputace: 0
Nejtěžší statisticky příklad na logiku
Dnes zadaný příklad je jedním z klasických příkladů, které vedly ke vzniku teorie pravděpodobnosti a statistiky. Řešen byl již v 16. století kdy nebyly rozvinuty potřebné nástroje.
Úkol 1
Když Titius pojal Caju za choť, byli otcové obou manželů živí a zámožní. Titius sepsal manželskou smlouvu tak, že narodí-li se z manželství děti a manželka zemře dříve než manžel, obdrží manžel ze společného majetku, jak oběma do manželství přineseného, tak děďictvím získáného:
Dvě třetiny, budou li otcové obou manželů oba živi nebo oba mrtvi.
Jednu polovinu, zemřel-li již Cajin otec, ale druhý bude ještě živ.
Tři čtvrtiny, zemře-li jeho otec, ale Cajin otec bude živ.
Zbytek dostanou děti.
Když se však Cajiným rodičům zdál poslední článek nespravedlivý, navrh budoucí zeť, aby bez rozlišování jednotlivých případů vše bylo shrnuto do jednoho článku tak, že vdovec dostane dvě třetiny, ať je jakákoliv budoucnost rodičů manželů. Cajin otec souhlasil.
Je otázka, zda manželská smlouva sepsaná druhým způsobem je příznivější Cajiným dětem než první, kterou původně navrhoval Titius a kterou odmítl Cajin otec.
Předpokládejme, že pravděpodobnost úmrtí všech osob je totožná a dědictví obou otců je stejné.
Nápověda:
Za výhodnější považujeme tu smlouvu, u které je střední hodnota předpokládaného dědictví vyšší.
Označte si pomocí neznámých parametrů množství dědictví po otcích a množství společného majetku manželů.
Určete pravděpodobnostní funkci náhodné veličiny X udávající množství Titiem zděděného majetku.
Určete střední hodnotu náhodné veličiny X.
Mohl by mi prosím někdo pomoct vypočítat tento extra těžký příklad ? Jsem zvědavá, kolik lidí zvládne tohle vypočítat. Kdo bude první a správně vyřeší, ať mi napíše, pošlu odměnu nejlepšímu řešiteli.
Offline
#2 11. 04. 2018 16:44 — Editoval laszky (16. 07. 2022 23:27)
Re: Nejtěžší statisticky příklad na logiku
↑ Adélka Hrubá:
Ahoj. Pokud oznacime  pravdepodobnost umrti nektere z osob, potom stredni hodnota v prvnim pripade je
pravdepodobnost umrti nektere z osob, potom stredni hodnota v prvnim pripade je
[mathjax] EX = \sum_{i=1}^4x_ip_i = \frac{2}{3}p^2+\frac{2}{3}(1-p)(1-p)+\frac{1}{2}p(1-p)+\frac{3}{4}p(1-p) = \frac{2}{3}+\frac{1}{12}p(1-p) > \frac{2}{3},[/mathjax]
protoze [mathjax]p>0[/mathjax] a [mathjax]1-p>0.[/mathjax]
V prvnim pripade by tedy Titius ziskal v prumeru vice. Druha smlouva pro nej byla mene vyhodna.
Edit: Opravil jsem tu posledni nerovnost na opacnou. Diky ↑ Pritt: za upozorneni.
Offline
#3 12. 04. 2018 10:58
- Adélka Hrubá
- Zelenáč
- Příspěvky: 8
- Škola: SVSE Praha
- Pozice: Student
- Reputace: 0
Re: Nejtěžší statisticky příklad na logiku
Ahoj, nešlo by prosím rozvést, jak se dostat k jednotlivým číslům ?
Offline
#4 13. 04. 2018 10:01
Re: Nejtěžší statisticky příklad na logiku
Ahoj,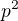 - pravděpodobnost, že umřou oba
- pravděpodobnost, že umřou oba - prav., že budou oba živí
- prav., že budou oba živí - prav., že první zemře a druhý bude naživu
- prav., že první zemře a druhý bude naživu - prav., že druhý zemře a první bude naživu
- prav., že druhý zemře a první bude naživu
Při výpočtu střední hodnoty se každý člen násobí částí zděděného majetku.
Offline
#5 13. 04. 2018 12:28
- Adélka Hrubá
- Zelenáč
- Příspěvky: 8
- Škola: SVSE Praha
- Pozice: Student
- Reputace: 0
Re: Nejtěžší statisticky příklad na logiku
Tisícere díky
Offline
#8 18. 04. 2018 16:18
- Adélka Hrubá
- Zelenáč
- Příspěvky: 8
- Škola: SVSE Praha
- Pozice: Student
- Reputace: 0
Re: Nejtěžší statisticky příklad na logiku
Ještě otázka, jaké množství zdědí ? Tahle otázka nebyla zodpovězena prosím
Offline

