Matematické Fórum

Al1 · 19. 04. 2018 19:18

Dobrý den,

potřebuji poradit s výpočtem $\int_{-1}^{1}\mathrm{acos}(x) \ dx$ , Použil jsem metodu per partes a v průběhu řešení je třeba vypočítat $\int_{-1}^{1}\frac{x}{\sqrt{1-x^{2}}} \ dx$ . Umím vypočítat neurčitý integrál $\int_{}^{}\frac{x}{\sqrt{1-x^{2}}}\ dx=-\sqrt{1-x^{2}}+c$ , takže s použitím tohoto výpočtu a dosazením mezí nemám problém a uirčitý integrál vychází nula.
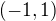Jde mi o to, že integrand není definovaný na $\langle-1,1\rangle$ , ale na $(-1,1)$ . Jak postupovat při výpočtu? Mohu udělat závěr, že integrand je funkce lichá a tudíž hned vím, že $\int_{-1}^{1}\mathrm{acos}(x) \ dx=0$

Děkuji.

laszky · 19. 04. 2018 21:58

Ahoj. Myslim, ze $\int_{-1}^{1}\mathrm{acos}(x) \ \mathrm{d}x=\int_{0}^{\pi}(1+\mathrm{cos}(x)) \ \mathrm{d}x=\pi$ - plyne napr. z graficke interpretace.

Co se tyce tveho postupu, zapomnel jsi, zes pouzil per partes:

$\int_{-1}^1 \mathrm{acos}(x)\ \mathrm{d}x = \left[x\mathrm{acos}(x)\right]_{-1}^1 + \int_{-1}^1\frac{x\ \mathrm{d}x}{\sqrt{1-x^2}} = \Bigr(0-(-\pi)\Bigr) + \Bigr[-\sqrt{1-x^2}\Bigr]_{-1}^1 = \pi$ .

Pokud jde o integral z neomezene funkce, po vhodne substituci se jedna v podstate o obdobu integralu $\int_0^1\frac{\mathrm{d}x}{\sqrt{x}} = \left[2\sqrt{x}\right]_0^1 = 2$ , ktery je konecny.

Al1 · 19. 04. 2018 22:06 — Editoval Al1 (19. 04. 2018 22:08)

↑ laszky:
Díky za odpověď. Já jsem na per partes nezapomněl, také píši, že jsem výpočet použil. Jde mi o to, že $\int_{-1}^{1}\frac{x}{\sqrt{1-x^{2}}} \ dx$ chci řešit substitucí $1-x^{2}=t^{2}$ a při přepočtu mezí si nevím rady. A nebo navrhni jinou substituci, se kterou nebudou "potíže".

laszky · 19. 04. 2018 22:25

Zrejme jde o to, ze funkce $1-x^2$ neni prosta na $[-1,1]$ a neni tedy invertibilni, coz je u substituce klicove - ptz by melo jit prejit inverzni substituci zpatky k puvodnimu integralu. Pokud integral roztrhnes na dva, substituci jiz pouzit muzes, ptz na dilcich intervalech je jiz fce $1-x^2$ prosta.

$\int_{-1}^{0}\frac{x}{\sqrt{1-x^{2}}} \ dx = \int_0^1\frac{-t\ \mathrm{d}t}{t} = -1$
$\int_{0}^{1}\frac{x}{\sqrt{1-x^{2}}} \ dx = \int_1^0\frac{-t\ \mathrm{d}t}{t} = -\int_0^1\frac{-t\ \mathrm{d}t}{t}=1$

Al1 · 19. 04. 2018 22:32

↑ laszky:
Tak tu myšlenku užít dva integrály jsem měl také, ale nedotáhl jsem ji do konce.
Mohu se ještě zeptat na tvůj výpočet $\int_{-1}^{1}\mathrm{acos}(x) \ \mathrm{d}x=\int_{0}^{\pi}(1+\mathrm{cos}(x)) \ \mathrm{d}x=\pi$
Proč 1+cos(x)?

laszky · 19. 04. 2018 22:43 — Editoval laszky (19. 04. 2018 22:49)

↑ Al1:

To je ciste z graficke interpretace. Kdyz chces spocitat plochu pod grafem funkce $\mathrm{acos}(x)$ od -1 do 1, tak je to stejne (zobrazis graf osove soumerne podle primky y=x) jako pocitat plochu pod grafem funkce $\cos(x)$ od 0 do $\pi$ , pricemz si ten graf musis jeste o 1 posunout na $1+\cos(x)$ , aby ta funkce byla kladna :-)