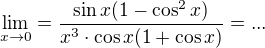Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 24. 04. 2018 23:47 Příspěvek uživatele kotry byl skryt uživatelem kotry. Důvod: duplikát
#5 24. 04. 2018 23:48 Příspěvek uživatele kotry byl skryt uživatelem kotry. Důvod: porušení pravidel fora
#7 25. 04. 2018 00:17
#8 25. 04. 2018 00:47
Re: Limita
↑ medvidek:
Díky, už to vychází. Poslední dva dny jsem nějak mimo, pořád dělám v příkladech takové hloupé chyby. Snad budu příští týden v lepší kondici, když mám maturovat :D.
Offline

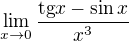

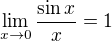 - jenže co s tím
- jenže co s tím  ?
?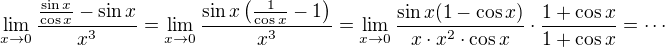
![kopírovat do textarea $\lim_{x\to0}=\frac{\sin x(1-\cos ^{2}x)}{x^{3}\cdot \cos x}=\lim_{x\to0}\frac{\sin ^{3}x}{x^{3}\cdot \cos x}=\lim_{x\to0}[(\frac{\sin x}{x})^{3}\cdot \frac{1}{\cos x}]=1^{3}\cdot \frac{1}{1}=1$](/mathtex/f2/f222e1f60218565623c6d00e29322e5d.gif)