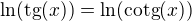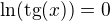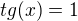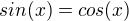Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 04. 05. 2018 09:27 — Editoval Peter_CSR (04. 05. 2018 09:27)
Re: Logaritmická rovnice
jkk777 napsal(a):
řešení
nemalo by to byt 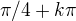 ?
?
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#5 04. 05. 2018 10:15
Re: Logaritmická rovnice
↑ Peter_CSR:
Zdravím,
↑ jkk777:
nenapsal, že řešením rovnice je 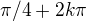 . To jen položil otázku, proč je u dané rovnice "kdesi" v oficinálních výsledcích uvedeno právě řešení
. To jen položil otázku, proč je u dané rovnice "kdesi" v oficinálních výsledcích uvedeno právě řešení 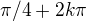 , když jemu vychází
, když jemu vychází 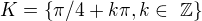 . A kolega ↑ laszky: mu potvrdil, že jeho řešení
. A kolega ↑ laszky: mu potvrdil, že jeho řešení 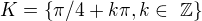 je správné- :-)
je správné- :-)
Offline
#7 04. 05. 2018 14:35
Re: Logaritmická rovnice
↑ Al1:
ako som povedal v predchadzajucoim prispevku, dakujem a sorry za tvoj cas :) . Polepsim sa, slibujem :)
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline