Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » doplnte cislo
#1 15. 05. 2018 09:26
doplnte cislo
Z casu na cas sa na forum dostane uloha typu "Doplnte dalsi clen postupnosti ...". Su v principe dve moznosti - v prvej moznosti je poskytnuta dalsia informacia alebo informacie o uvazovanej postupnosti. Vo velmi zjednodusenom priklade: "Doplnte treti clen aritmetickej postupnosti, ak jej prvy clen je 3 a druhy je 5." Ulohy takehoto typu su uplne v poriadku a teraz sa nimi nebudem zaoberat.
Druhym pripadom su situacie, ked o hladanej postupnosti nie je nic zname a presne take mam teraz na mysli. Sem tam ich mozete najst v roznych zabavnych rubrikach casopisov, v oblube ich maju tvorcovia "IQ testov" a co povazujem za kriticke, objavuju sa aj v prijimacich testoch na vysoke skoly. Dovolim si tvrdit, ze taketo ulohy nemaju v serioznej matematike co hladat a deformuju predstavy verejnosti o matematike. Univerzalnym principom riesenia matematickych problemov su (pri velkom zjednoduseni) dva kroky:
1. Najst riesenie
2. Ukazat, ze ine riesenie uz neexistuje.
Druhy krok velmi casto v rieseni explicitne nevystupuje, pretoze je napriklad zrejmy z pouziteho postupu. To ale neznamena, ze ho mozeme ignorovat. A zasadnym problemom spominanej kategorie uloh je to, ze druhy krok pri nom nie je mozne urobit. Ak mame doplnit stvrty clen postupnosti, v ktorej prve tri cleny su  , tak na stvrtom mieste moze byt akekolvek realne cislo
, tak na stvrtom mieste moze byt akekolvek realne cislo  , pretoze existuje postupnost, ktorej prve styri cleny su
, pretoze existuje postupnost, ktorej prve styri cleny su  , dokonca takych postupnosti existuje nekonecne vela.
, dokonca takych postupnosti existuje nekonecne vela.
Tvorcovia podobnych uloh a ich obhajcovia budu zrejme tvrdit, ze "ide o najdenie pravidla, pomocou ktoreho boli prve tri cleny vytvorene". Takato argumentacia ale neobstoji. Napriklad aj uvedene cleny  mozu byt prvymi tromi clenmi aritmetickej postupnosti a v tom pripade stvrty clen bude
mozu byt prvymi tromi clenmi aritmetickej postupnosti a v tom pripade stvrty clen bude  , ale aj postupnosti vsetkych neparnych prvocisel, a teda stvrty clen bude
, ale aj postupnosti vsetkych neparnych prvocisel, a teda stvrty clen bude  .
.
Tvorcovia a obhajcovia takychto uloh mozu namietat, ze okrem tychto dvoch rieseni sa ine neponuka, ale nemaju pravdu. V prvom rade - staci poznat definiciu postupnosti, aby sme pochopil, ze stvrty clen moze pokojne byt  . Uloha je splnena, pretoze postupnost s takymi styrmi prvymi clenmi skutocne existuje. V definicii postupnosti nie je ani slovo o tom, ze by sa jej
. Uloha je splnena, pretoze postupnost s takymi styrmi prvymi clenmi skutocne existuje. V definicii postupnosti nie je ani slovo o tom, ze by sa jej  -ty clen mal dat zapisat pomocou akejsi formuly na zaklade znalosti predchadzajucich clenov.
-ty clen mal dat zapisat pomocou akejsi formuly na zaklade znalosti predchadzajucich clenov.
A mimochodom, pre lubovolnu volbu hladaneho clena taka formula existuje - dokonca ide o polynomicku funkciu.
Co teda s takymito ulohami? Ak ste v pozicii, ze ich vyskyt mozete redukovat, prosim urobte to. Zvlast ak ide o prijimacie alebo skusobne testy na skolach akehokolvek typu - tam skutocne nemaju co robit. Ak ste student a takuto ulohu ste dostali v skole, upozornite prosim vhodnou formou vyucujuceho, ze ide o ulohu s nekonecnym poctom rieseni, z ktorych kazde je "rovnako dobre".
Dakujem.
Offline
#2 15. 05. 2018 09:44 — Editoval vanok (15. 05. 2018 10:25)
Re: doplnte cislo
Pozdravujem ↑ vlado_bb:,
Tema na rozmyslanie.
Kolega ↑ vlado_bb: ma podla mna pravdu.
A zaujimat sa napr. o postupnosti moze byt skutocna matematicka aktivita. Poznate toto url http://oeis.org ?
Zaujimave, ze.
Edit. Tu http://forum.matweb.cz/viewtopic.ph … 2&p=12 v #298 je zaujimave citanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 15. 05. 2018 19:22
Re: doplnte cislo
Utery 15. kvetna 1584, Pisa, Toskansko, dnesni Italie:
Jiz po ste se splha student mistni univerzity do sedmeho patra veze s bednou tezkych delovych kouli rozlicnych hmotnosti a haze je dolu. Dole, na miste dopadu, jiz vznika maly krater. Pak se ale student najednou zamysli: "K cemu mi je sto pokusu, kdyz stoprvni muze beztak dopadnout uplne jinak. Jdu se radsi venovat nabozenstvi, to ma vetsi budoucnost."
Strih.
Utery 15. zari 1665, Woolsthorpe-by-Colsterworth, Lincolnshire, dnesni Anglie:
Po vydatnem obede se mlady clen Trinity College natahl do stinu jablone a usnul. Kdyz najednou zafouka vitr a z koruny jablone na jeho hlavu spadne jablko. "I co, asi nejaka nahoda", rekne si. O dve hodiny pozdeji jiz kolem nej lezi sto jablek a na jeho hlave je sto bouli, presto dospeje k nazoru, ze "Sto jablek spadlo na moji hlavu ze stromu, ale to stoprvni muze beztak nekam odletet a na zem (hlavu) nespadne. Jdu se radsi venovat nabozenstvi, to ma vetsi budoucnost"
Strih
Utery 15. brezna 1825, Erlangen, Bavorsko, dnesni Nemecko:
Syn zamecnika dela pokusy s draty, skrz ktere pousti elektricky proud. Ackoli jiz vyzkousel stovku dratu ruznych delek a sirek vyrobenych z ruznych materialu a z namerenych hodnot by snad i slo vydedukovat nejaky vztah, pomysli si: "K cemu mi je sto pokusu, kdyz ten stoprvni stejne muze dopanout uplne jinak. Jdu se radsi venovat nabozenstvi, to ma vetsi budoucnost."
Strih
Utery 15. prosince 1942, Chicago, Illinois, USA:
Italsky emigrant ostreluje pomoci neutronu atomy uranu a pozoruje jejich rozpad a uvolnujici se energii. Kdyz v tom si rekne: "Ze sta provedenych pokusu by snad slo vytusit nejakou zavislost, ale stoprvni muze beztak dopadnout uplne jinak. Toho Hitlera porazime urcite jinak. Jdu se radsi venovat nabozenstvi, to ma vetsi budoucnost."
Strih
Utery 15. kvetna 2018, diskuzni internetove forum.
Ulohy, kde by se z nekolika cisel mela dedukovat nejaka zavislost, by se mely redukovat. Urcite to nepatri do skol.
Offline
#5 15. 05. 2018 21:11
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: doplnte cislo
↑ laszky:
Ahoj, rozdíl mezi posledním a ostatními přiklady je ten, že u ostatních je znám kontext, odkud se ta čísla vzala - tj. že je dána nějaká zkoumaná veličina, příklady jejích hodnot, a je možné zkoumat nejen tyto hodnoty, ale i onu veličinu.
Střih:
Průměrný student matematiky si prohlíží IQ test a vidí úlohu: Jakým číslem pokračuje následující posloupnost? 1,2,4,8,16, ... Zvolí 32.
Střih:
Student matematiky s oblibou v číselných soustavách si prohlíží IQ test a vidí úlohu: Jakým číslem pokračuje následující posloupnost? 1,2,4,8,16, ... Zvolí 23. Každé následující číslo je totiž dáno jako součet číslic přechozích čísel zvětšený o 1.
Střih:
Student matematiky s oblibou v kombinatorické geometrii si prohlíží IQ test a vidí úlohu: Jakým číslem pokračuje následující posloupnost? 1,2,4,8,16, ... Zvolí 31. Číslo na n-té pozici totiž označuje maximální počet oblastí kružnice, které vytnou úsečky spojující n bodů na obvodu této kružnice.
"Máte úhel beta." "No to nemám."
Offline
#6 15. 05. 2018 21:15
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: doplnte cislo
Ahoj, já bych řekl, že je rozdíl mezi úlohou:
vlado_bb napsal(a):
"doplnte dalsi clen v postupnosti
"
a úlohou
"doplnte dalsi clen v postupnosti  , kde uvedené hodnoty jsou vdálenosti, které urazil přemět spuštěný z věže za 1,2,3,4 sekundy"
, kde uvedené hodnoty jsou vdálenosti, které urazil přemět spuštěný z věže za 1,2,3,4 sekundy"
"Máte úhel beta." "No to nemám."
Offline
#8 15. 05. 2018 21:33
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: doplnte cislo
↑ MichalAld:
Kromě toho, že jde o první číslice čísla pi, tak třeba: lze si snadno všimnout, že na sudých místech je vždy 1 a že čísla na lichých místech tvoří atimetickou posloupnost s diferencí 1, takže posloupnost pokračuje jako 1,6,1,7,..
A pak je otázka - které řešení je správné a které je jednodušší? :-)
"Máte úhel beta." "No to nemám."
Offline
#9 15. 05. 2018 21:41
Re: doplnte cislo
Ahoj ↑ MichalAld:,
Oeis nasiel taketo postupnosti v ktorych najdes tvoju postupnost aj v situaciach, ze nejde o zaciatocne cleny postupnosti
http://oeis.org/search?q=3%2C+1%2C+4%2C … ;go=Search
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 15. 05. 2018 22:49
Re: doplnte cislo
↑ MichalAld:
Pozdravujem, a ja mam rad ↑ vanok: tu co som tam pridal v edit.
Ze to je krasne.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 16. 05. 2018 11:04
Re: doplnte cislo
Ahoj ↑ MichalAld:,
To neviem. Ako by si to dokazal?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 16. 05. 2018 15:44
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: doplnte cislo
check_drummer napsal(a):
Střih:
Student matematiky s oblibou v číselných soustavách si prohlíží IQ test a vidí úlohu: Jakým číslem pokračuje následující posloupnost? 1,2,4,8,16, ... Zvolí 23. Každé následující číslo je totiž dáno jako součet číslic přechozích čísel zvětšený o 1.
Vedel by si nájsť kontrapríklad aj na postupnosť zadanú 1,2,4,8,16,32,...?
check_drummer napsal(a):
Střih:
Student matematiky s oblibou v kombinatorické geometrii si prohlíží IQ test a vidí úlohu: Jakým číslem pokračuje následující posloupnost? 1,2,4,8,16, ... Zvolí 31. Číslo na n-té pozici totiž označuje maximální počet oblastí kružnice, které vytnou úsečky spojující n bodů na obvodu této kružnice.
Platí to aj pre n=1?
Offline
#14 16. 05. 2018 16:34
Re: doplnte cislo
Ahoj ↑ Ferdish:,
To je otazka interpretacie. ( alebo priliz rychlej redakcie popisu takej situacii)
Jeden bod neurcuje nejaku priamku ( ta je urcena dvomi roznymi bodmi).
Tak pre jeden dany bod na kruznici jej zodpovedajuca cast kruhu ktory urcuje ma jedinu oblast.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 16. 05. 2018 16:42 — Editoval Ferdish (16. 05. 2018 16:48)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: doplnte cislo
Ahoj ↑ vanok:,
áno, išlo mi o to, ako je možné pomocou úsečky spojiť bod so sebou samým :)
Samozrejme, v niektorých prípadoch býva samotný bod považovaný za úsečku s nulovou dĺžkou, ale to už potom IMO skĺzneme do dišputy nie nepodobnej tej o štvorci ako o limitnom prípade obdĺžnika.
Offline
#16 16. 05. 2018 20:31
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: doplnte cislo
Ahoj,
Ferdish napsal(a):
check_drummer napsal(a):
Střih:
Student matematiky s oblibou v číselných soustavách si prohlíží IQ test a vidí úlohu: Jakým číslem pokračuje následující posloupnost? 1,2,4,8,16, ... Zvolí 23. Každé následující číslo je totiž dáno jako součet číslic přechozích čísel zvětšený o 1.Vedel by si nájsť kontrapríklad aj na postupnosť zadanú 1,2,4,8,16,32,...?
Asi ano - třeba se studentem, který má rád Lagrangeův interpolační polynom. :-)
Ferdish napsal(a):
check_drummer napsal(a):
Střih:
Student matematiky s oblibou v kombinatorické geometrii si prohlíží IQ test a vidí úlohu: Jakým číslem pokračuje následující posloupnost? 1,2,4,8,16, ... Zvolí 31. Číslo na n-té pozici totiž označuje maximální počet oblastí kružnice, které vytnou úsečky spojující n bodů na obvodu této kružnice.Platí to aj pre n=1?
Proč by neplatilo? Zůstane pouze jediná oblast - celá plocha kružnice - více oblastí tam být nemůže. :-)
"Máte úhel beta." "No to nemám."
Offline
#17 16. 05. 2018 21:03
Re: doplnte cislo
Ahoj ↑ check_drummer:,
A ako si si mohol vsimnut, v priklade co som citoval vyssie ↑ vanok: najdes podobnu situaciu, no dve rozne postupnosti sa lisia prvy krat v clenoch 777451915729367 .
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#18 16. 05. 2018 22:39
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: doplnte cislo
↑ check_drummer:
Ak mi nájdeš stredoškoláka, ktorý si sám od seba naštudoval LIP a našiel v ňom životné zaľúbenie, tak OK :-)
A čo sa týka tej druhej citácie, išlo mi o tú úsečku, ktorou spojíš bod so sebou samým...tak ako som spomenul vyššie.
Offline
#19 17. 05. 2018 09:05
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: doplnte cislo
↑ Ferdish:
I kdybys spojil úsečkou bod se sebou samým, tak nezískáš další oblasti.
A jak souvisí neznalost LIP s nejednoznačným řešením problému? Sám jsi psal, že se při zadání této úlohy nesmí radit, jaký tvar má ta závislost, takže mi z toho plyne, že se ani nesmí radit, že se nesmí použít LIP. :-)
Takže paradoxně studenti s vyšší znalostí budou více penalizovaní, protože budou uvažovat i složitější vztahy, které by zadavatel nezvolil a možná je ani nezná..
"Máte úhel beta." "No to nemám."
Offline
#20 17. 05. 2018 09:31 — Editoval Ferdish (17. 05. 2018 11:49)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: doplnte cislo
↑ check_drummer:
No, akurát penalizujú samých seba, pretože uvažovanie zložitejších vzťahov ich bude pri riešení stáť viacej času, ktorý im potom môže chýbať inde...kdežto postupnosť n-tých mocnín čísla 2, kde 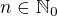 intuitívne napadne väčšinu. Znovu hovorím - Occamova britva.
intuitívne napadne väčšinu. Znovu hovorím - Occamova britva.
Offline
#21 17. 05. 2018 11:44
Re: doplnte cislo
Pozdravujem,
Dam tu priamo to url o ktorom som uz tu pisal, ale asi ste ho nenasli ( skoda) http://ami.ektf.hu/uploads/papers/final … 9to234.pdf
Oplati sa precitat.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#22 17. 05. 2018 22:48
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: doplnte cislo
↑ Ferdish:
Jakým číslem pokračuje tato posloupnost:
1, ..
?
"Máte úhel beta." "No to nemám."
Offline
#24 18. 05. 2018 08:46
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: doplnte cislo
↑ check_drummer:
Tak toto je už vážne pod moju úroveň...s tebou sa skutočne nedá debatovať. Končím.
Offline
#25 18. 05. 2018 15:44
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: doplnte cislo
↑ check_drummer:
Pokud máš jenom jedno číslo, tak nejjednodušší je jeho opakování, tj. 1,1,1,...
Tyhle druhy testů testují (očividně):
1. Schopnost vidět vzory v datech.
2. Najít pravidlo, které je s nejvyšší pravděpodobností zodpovědné za generování toho vzoru.
Je to inteligence (nebo alespoň jeden z druhů inteligence) a prediktor schopnosti studovat.
Ale pochopitelně nemůže existovat žádný algoritmus, který by tohle řešil obecně.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » doplnte cislo