Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 05. 2018 17:46
Určení hodnot parametrů kvadratické rovnice
Ahoj, prosím o pomoc,
ve vzorových přijímačkách na ČVUT je tento příklad:
Určete hodnotu parametrů a, b, c tak, aby rovnost
(2a - 3x)(by + 3) = 9x^2 + 2cx + 2
platila pro každé reálné číslo x, a rozhodněte, které tvrzení je pravdivé.
A) Existuje více trojic parametrů splňujících podmínky
B) Součin všech parametrů je 11/2
C) a = 3, b = -3, c = 11/2
D) Takové parametry neexistují
E) Žádná z ostatních možností není správná
Offline
#2 22. 05. 2018 18:05
Re: Určení hodnot parametrů kvadratické rovnice
Já bych to viděl asi takto:
Pokud by to mělo mít řešení, musel bys volbou parametrů dosáhnout toho, že levá strana bude stejná jako pravá.
Levá strana obsahuje proměnnou y (to není parametr) a pravá ne. Takže dokud tam bude to y, tak to nemůže být splněno nikdy. Toho y se ale můžeme zbavit tak, že položíme b=0.
Dále na pravé straně je člen 9x^2, a na levé žádné x^2 nemáme. Žádnou volbou nedosáhneme toho, aby nám na pravé straně tento člen zmizel, nebo se na levé objevil.
PS: není to y náhodou chyba, nemá tam být taky x ?
Offline
#3 22. 05. 2018 18:34
Re: Určení hodnot parametrů kvadratické rovnice
↑ MichalAld:
Omlouvám se, skutečně místo (by + 3) má správně být (bx+ 3) .
Když se vše vykrátí, vyjde
(9 + 3b)x^2 + (2c - 2ab + 9)x + (2 - 6a),
ale nevím jak postupovat dál.
Offline
#4 22. 05. 2018 18:40
Re: Určení hodnot parametrů kvadratické rovnice
↑ re_visor:
Přesněji řečeno, vyjde
(9 + 3b)x^2 + (2c - 2ab + 9)x + (2 - 6a) = 0
Offline
#5 22. 05. 2018 18:42 — Editoval Peter_CSR (22. 05. 2018 18:43)
Re: Určení hodnot parametrů kvadratické rovnice
...pripominas mi Kubasa :)
obecne, rovnica ma nekonecne vela rieseni ked 0x = 0.
...resp. pre kvadraticku rovnicu musi zjavne platit ze 
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#6 22. 05. 2018 19:33
Re: Určení hodnot parametrů kvadratické rovnice
↑ Peter_CSR:
Kubase neznám :)
Znamená to, že existuje jen jediné řešení a to: a= b = c = 0 ?
Offline
#7 22. 05. 2018 19:54
Re: Určení hodnot parametrů kvadratické rovnice
↑ re_visor:
Ne, to znamená, že řešení najdeš vyřešením soustavy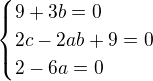
(pokud je tvůj příspěvek #4 správně - nekontroloval jsem)
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#8 22. 05. 2018 20:17 — Editoval Al1 (22. 05. 2018 20:21)
Re: Určení hodnot parametrů kvadratické rovnice
↑ re_visor:
Zdravím,
v zadání je napsáno: Určete hodnotu parametrů a, b, c tak, aby rovnost ... Dívej se na příklad jako na rovnost dvou kvadratických trojčlenů. A ty se rovnají, pokud se rovnají jednotlivé koeficienty.
Po úpravě levé strany dostaneš 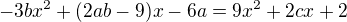 . A z toho ti plyne to, co napsal kolega ↑ zdenek1:.
. A z toho ti plyne to, co napsal kolega ↑ zdenek1:.
Ona totiž kvadratická rovnice nemůže mít nekonečně mnoho řešení, jak ti naznačil ↑ Peter_CSR:.
Edit: a tvé téma patří do sekce SŠ. :-)
Offline
