Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 05. 2018 22:24 — Editoval Peter_CSR (24. 05. 2018 22:25)
zvájomná poloha priamok v priestore
Zdravíčko,
majme 2 priamky v  :
:
p:  ,
, 
q:  ,
, 
Ako zistím ich vzájomnú polohu užitím hore uvedených rovníc?
Mohol by som vytypovať nejaké body  patriace každej priamke, určiť smerový vektor, napísať parametrické rovnice a tie porovnať, ale tento postup nechcen. Chcel by som využiť pramo všeobecné rovnice.
patriace každej priamke, určiť smerový vektor, napísať parametrické rovnice a tie porovnať, ale tento postup nechcen. Chcel by som využiť pramo všeobecné rovnice.
Ďakujem.
- Pepe the Frog
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#2 24. 05. 2018 23:24 — Editoval Ferdish (24. 05. 2018 23:26)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: zvájomná poloha priamok v priestore
Priamka sa v  nedá zapísať všeobecne, len parametricky. Takže mi nejako uniká, ako chceš dospieť k riešeniu IBA s použítím všeobecných rovníc...
nedá zapísať všeobecne, len parametricky. Takže mi nejako uniká, ako chceš dospieť k riešeniu IBA s použítím všeobecných rovníc...
Offline
#3 24. 05. 2018 23:32 — Editoval misaH (24. 05. 2018 23:33)
- misaH
- Příspěvky: 13459
Re: zvájomná poloha priamok v priestore
↑ Ferdish:
Ahoj.
:-)
Dá sa zapísať ako prienik dvoch rovín, to je všeobecný zápis.
(A veď keď chce, tak ho nechaj, nech rieši...)
Offline
#4 24. 05. 2018 23:41 — Editoval laszky (25. 05. 2018 09:52)
Re: zvájomná poloha priamok v priestore
↑ Peter_CSR:
Rovnice lze zapsat jako soustavu 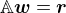 , kde
, kde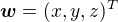 ,
, 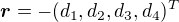 a
a  .
.
Predpokladejme, ze oba dva pary rovnic skutecne definuji primky, pak se jedna o soustavu 4 rovnic o trech neznamych s matici  splnujici
splnujici 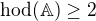 . Ta muze mit 0, 1, nebo nekonecne mnoho reseni:
. Ta muze mit 0, 1, nebo nekonecne mnoho reseni:
a) Pokud 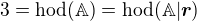 , ma podle Frobeniovy vety soustava prave jedno reseni a primky jsou tedy ruznobezky lezici v jedne rovine.
, ma podle Frobeniovy vety soustava prave jedno reseni a primky jsou tedy ruznobezky lezici v jedne rovine.
b) Pokud 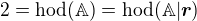 , potom jsou primky totozne.
, potom jsou primky totozne.
c) Pokud  , potom jsou primky rovnobezne ruzne.
, potom jsou primky rovnobezne ruzne.
d) Pokud  , potom jsou primky mimobezne.
, potom jsou primky mimobezne.
Offline
#5 25. 05. 2018 00:11
Re: zvájomná poloha priamok v priestore
↑ laszky:
vvvďaka...! Pozriem si tú Frobeniovu vetu, snáď to nebude zase nejaké maso :D Medzitým, čo značí to malé roztomilé T-čko nad vektormi?
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#7 25. 05. 2018 00:38 — Editoval Peter_CSR (25. 05. 2018 00:40)
Re: zvájomná poloha priamok v priestore
↑ Ferdish:
Skutočne je tomu tak. Ja som ich ale zapísal ako prienik nadrovín.
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#8 25. 05. 2018 01:37
Re: zvájomná poloha priamok v priestore
↑ laszky:
oh, aha! T-ako transformovaný! Ha! (však?)
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#9 25. 05. 2018 01:43
#10 25. 05. 2018 02:19
Offline
 ;-)
;-)