Matematické Fórum

Peter_CSR

Zdravíčko,

majme úlohu:

Za stôl s 10 miestami, u ktorého jednoznačne rozoznávame každé miesto, musíme usadiť 5 mužov, 3 ženy, 2 mačky a psa.

Muži neznášajú iných mužov a mačky (konkurencia a nemajú radi to malé chlpaté "mňau") a ženy neznášajú iné ženy a psov.

Ako úlohu riešiť?

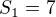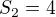Mohol by som mužov a mačky zgrupovať do jednej skupiny a ženy a psov do druhej. Tým pádom dostanem skupinu $S_{1} = 7$ a $S_{2} = 4$ Najskôr musím rozdeliť stôl na Skupinu 1 a Skupinu 2, ktoré sa budú striedať, čiže sa jedná o permutácie 2. triedy bez opakovania. Následne, keď viem poradie skupín chcem určiť ktoré miesta sa obsadia: V skupine 1 mám 7 prvkov na 5 miest, takže sa obsadia všetky (kombinujem... na 5 miest 5 rôznych prvkov), v skupine 2 mám 4 prvky, takže mužomačky budú sedieť buď vedľa ženopsov alebo vedľa prázdneho miesta. Jedná sa teda o kombinácie 4.triedy z 5 prvkov. No a keď mám všetky miesta vybraté, vyberem kto ich obsadí: v prvej skupine to bude variácia 5. triedy zo 7. prvkov, v druhej permutácia 4 prvkov.

Výsledná rovnica bude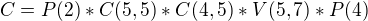

$C = P(2)*C(5,5)*C(4,5)*V(5,7)*P(4)$

uhm... je to takto správne?

zdenek1 · 25. 05. 2018 05:44

↑ Peter_CSR:
To jako umístíš na deset míst jedenáct "věcí"? Někdo bude mít kočku na klíně? Nebo bude pes pod stolem?
Úloha není dost exaktně zadaná.

Peter_CSR · 25. 05. 2018 11:32

↑ zdenek1:

samozrejme sa na 10 miest zmestí maximálne 10 osôb. V riešení som napísal, že používam variácie 5. triedy zo 7 prvkov, správne? Muži a mačky nemôžu sedieť vedľa seba, takže bude vedľa nich buď žena, mačka alebo prázdna sedačka.

Ale rozumiem, týmto kombinátorickým úlohám je vždy ťažké porozumieť. Už vidím prečo.

Ferdish

↑ Peter_CSR:
Kolega ↑ zdenek1: podľa mňa reagoval na to, že či zvieratá berieš ako neoddeliteľný doplnok k už sediacemu mužovi alebo žene (teda že samotný pes/samotná mačka nemôže obsadiť voľné miesto) alebo nie.

laszky · 25. 05. 2018 12:56

↑ Peter_CSR:

Kdyz muze byt jedno prazdne misto, muzou byt i 2? Muze byt 9 prazdnych mist?

Peter_CSR · 26. 05. 2018 00:04

↑ Ferdish:

:D :D :D Tak to ma naozaj nenapadlo :D

úloha bola myslená ako pohranie sa s rôznymi podmienkami, je to obdoba problému Okrúhleho stola. Okrúhli stôl počíta len so ženami a mužmi, ja som uvažoval o rozšírení o ďalšie kategórie, ale to by iba znamenalo zmenu rozšírenia počtu "sekcií"...myslím....

Keď nad tým tak premýšlam, úloha by sa dala ešte riadne zkomplikovať, ale asi to zatiaľ robiť nebudem... mám v hľadáčiku momentálne iné problémy... Len ma zaújmalo či moje uvažovanie bolo správne, ale myslím že áno.

Peter_CSR · 26. 05. 2018 00:08

laszky napsal(a):
↑ Peter_CSR:

Kdyz muze byt jedno prazdne misto, muzou byt i 2? Muze byt 9 prazdnych mist?

Myslím, že v mojej úlohe výjde 1 prázdne miesto a 2 ľudia (z množiny mužomačiek) budú proste stáť vedľa (napríklad obsluhovať hostí). v úlohe ako som podal, nevidím spôsob, ako by si mohol jeden z nich sadnúť... Úloha by sa asi dala obmeniť a zkomplikovať, zatiaľ to asi robiť nebudem... dnes bojujem s elipsami a lin algebrou...

Každopádne vďaka za reakcie :)

Matematické Fórum

#1 25. 05. 2018 02:37 — Editoval Peter_CSR (25. 05. 2018 02:37)

Hrátky s kombinátorikou

#2 25. 05. 2018 05:44

Re: Hrátky s kombinátorikou

#3 25. 05. 2018 11:32

Re: Hrátky s kombinátorikou

#4 25. 05. 2018 11:41 — Editoval Ferdish (25. 05. 2018 11:42)

Re: Hrátky s kombinátorikou

#5 25. 05. 2018 12:56

Re: Hrátky s kombinátorikou

#6 26. 05. 2018 00:04

Re: Hrátky s kombinátorikou

#7 26. 05. 2018 00:08

Re: Hrátky s kombinátorikou

laszky napsal(a):

Zápatí