Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 05. 2018 00:00
Vzájomná poloha rovín v priestore
Zdravíčko,
takže: 
v a) a b) prípade je vidieť že normálové vektory rovín sú totožné, ostáva teda len zistiť či he posunutie oboch rovín zhodné alebo nie. OK.
c) som ale úplne neporozumel... 2 roviny majú v priestore prienik v priamke (mmch, 2 roviny v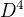 
sa môžu pretínať v bode. Viete si to predstaviť a vysvetliť? Ha! Ja áno! :) ), najjednoduchšia cesta ako túto priamku určiť vidím ako nájsť dve rôzne body, ktoré patria prieniku a z nicjh už určím smerový, normálový vektor a možem určiť rovnicu.
Riešeniu hore som ale úplne neporozumel... uuhm...Tie dve rovnice pod sebou sú zároveň jednoznačným vyjadrením priamky. Fajn. Zo zetovej súradnice sme spravili parameter a potom vyjadrili x,y...? Čo? Uhm... parameter je vlastne taká vecička, ktorá mi vraví "súradnica každého bodu na priamke je nejaký bod na priamke + parameter-krát jej smerový vektor"....Uuhm... proster do toho nevidím.
Vysvetlil by mi to niekto, prosím?
Ďakujem!
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#2 25. 05. 2018 09:20 — Editoval Ferdish (28. 05. 2018 15:28)
- Ferdish
- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Vzájomná poloha rovín v priestore
Podľa jedného z dôsledkov Frobeniovej vety - viď jedna z tvojich tém o vzájomnej polohe priamok - ak je počet neznámych n väčší než hodnosť matice systému (počet LN riadkov sústavy rovníc) k, tak sústava má nekonečne veľa riešení (v našom prípade trojíc [x,y,z]), ktoré možno vyjadriť pomocou n-k parametrov.
Máš n=3 (x,y,z) ale len 2 rovnice ktoré ich určujú (rovnice rovín) a tie sú lineárne nezávislé, takže k=2. Potrebuješ teda n-k=3-2=1 parameter.
Parameter si vo všeobecnosti môžeš zvoliť ľubovoľne, pokojne aj tak, že hodnotu parametra položíš rovnú hodnote jednej z tvojich neznámych. V tvojom prípade si vybrali neznámu z.
Offline
#3 26. 05. 2018 01:33
Re: Vzájomná poloha rovín v priestore
↑ Ferdish:
yop, ďakujem! Pozriem sa na Frobeniovu vetu ako ste obaja doporúčali len čo bude trocha času. Potom sa k topiku vrátim :)
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline