Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 06. 2018 12:35
- nikolka74123

- Zelenáč
- Příspěvky: 12
- Reputace: 0
Dělitelnost
Dobrý den, potřebovala bych obecně odvodit společné kritérium dělitelnosti čísly 41 a 271 když víte, že: 41*271*9=10^5-1 Děkuji...
Offline
- (téma jako vyřešené označil(a) nikolka74123)
#2 25. 06. 2018 15:19 — Editoval vanok (25. 06. 2018 15:35)
Re: Dělitelnost
Ahoj ↑ nikolka74123:,
Tuto ak chces overit, ze velke cislo N je delitelne cislom 41 alebo cislom 271 staci ze ho nahradis cislom rozdelenim na useky dlzky 5 ( smerom od jednotiek) a ich scitas. Dostanes cislo  .
.
Cisla N a  su sucasne delitelne cislom 41 ( ci cislom 271).
su sucasne delitelne cislom 41 ( ci cislom 271).
Dokaz ti necham urobit a aj generalizovat na ine situacie. (Aj aj na ine ciselne sustavy).
Ak treba podrobnosti mozem upresnit....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 26. 06. 2018 09:49
- nikolka74123

- Zelenáč
- Příspěvky: 12
- Reputace: 0
Re: Dělitelnost
Dobrý den, já bych právě potřebovala vědět, jak jste se k tomuto postupu dopracoval. Děkuji
Offline
#5 26. 06. 2018 11:54
- nikolka74123

- Zelenáč
- Příspěvky: 12
- Reputace: 0
Re: Dělitelnost
Tak ted už jsem úplně mimo :( čísla a,b jsou co za čísla?
Offline
#6 26. 06. 2018 12:17
Re: Dělitelnost
↑ nikolka74123:
Tak treba
Ale protoze  a
a ,
,
je cislo 5432112345 delitelne 41 i 271.
Offline
#7 26. 06. 2018 12:24
- nikolka74123

- Zelenáč
- Příspěvky: 12
- Reputace: 0
Re: Dělitelnost
Už rozumím děkuji :) a bude to stačit jako odůvodnění toho kritéria dělitelnosti?
Offline
#8 26. 06. 2018 15:47 — Editoval jarrro (26. 06. 2018 15:51)
Re: Dělitelnost
↑ nikolka74123: sú celé čísla. Z toho potom vidno, že ak
sú celé čísla. Z toho potom vidno, že ak 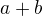 je deliteľné 41 alebo 271 tak aj
je deliteľné 41 alebo 271 tak aj  má takú vlastnosť a tiež naopak.
má takú vlastnosť a tiež naopak.
Prirodzené je predpokladať, že 
Ak potom vyjde (pre skúmané  )
)  možno na neho znovu použiť danú úvahu.
možno na neho znovu použiť danú úvahu.
CBTD.
MATH IS THE BEST!!!
Offline
#9 26. 06. 2018 16:43 — Editoval vanok (27. 06. 2018 08:44)
Re: Dělitelnost
Poznamka.
Na dokaz, mozes pouzit to, ze kriterium co som popisal plati, ak cislo na vysetrenie uvazujes v bazi 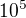 .
.
Doplnok. Ine kriteria https://en.m.wikipedia.org/wiki/Divisib … erion_1-11
https://www.cut-the-knot.org/blue/divisibility.shxtml
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

