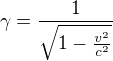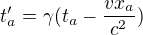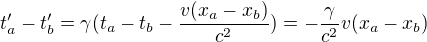Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#126 20. 06. 2018 17:19
Re: Relativita Soucasnosti
Zvedavec 4 napsal(a):
MichalAld napsal(a):
Máme dvě nesoučasné události, v určité vzdálenosti od sebe. Jako třeba že jede auto po dálnici, v určitém místě zatroubí (první událost) a o sto metrů dále zatroubí znovu (druhá událost). Události jsou zjevně nesoučasné a zjevně i v určité vzdálenosti od sebe. V soustavě spojené se silnicí.
Nyní hledáme soustavu (která se nějak pohybuje) takovou, aby se vlivem "určité rychlosti" události staly soumístné (na jednom místě). No shodou okolností je to zrovna ta soustava spojená s jedoucím autem. Pro řidiče auta nastaly události na stejném místě (klakson má pořád na stejném místě, někde pod kapotou).
Asi se lehce opakuji, ale tohle je přesně příklad, když se někdo snaží pochopit relativitu při vysokých rychlostech a ještě nepochopil tu relativitu při rychlostech nízkých.To se mi zda moc jako vtipnej trik. Muze v nem byt neco pravdy, to se musi nechat, ale problem bude, ze v tomhle pripade by to platilo pri jakekoliv rychlosti, tedy porad, a tak to snad odporuje definici RS.
Tohle (jak jsi situaci popsal) se ovšem netýká "relativity současnosti" ale tak zvané "relativity soumístnosti". Ten pojem se ovšem moc (vůbec) nepoužívá, protože asi každému (kromě tebe) to přijde úplně samozřejmé.
Offline
#127 21. 06. 2018 01:55 — Editoval Zvedavec 4 (23. 06. 2018 02:30)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Relativita Soucasnosti
Lukasi, podivejme se na tenhle tvuj priklad:
LukasM napsal(a):
1) Pokud se me kyvadlo kyve s periodou 10s, potom pri pohledu z "pohybující se" soustavy bude toto kyvadlo mít periodu 20s.
Tohle znamena, ze vzajemna rychlost mezi moji a tou "pohybující se" soustavou zapricini gamu=2.
Taky to znamena, ze cas se tim zpomali v te druhe soustave, jak z meho, tak i z jejiho hlediska, dvakrat.
Proto to taky potrva tomu druhemu kyvadlu, z obou hledisek, 2x tolik casu aby kyvlo jednou.
LukasM napsal(a):
2) Jestli maji v te druhe "pohybujici se" lodi nejake sve kyvadlo, co ma, z jejich hlediska periodu 5s, tak z pohledu te prvni, tedy me puvodni lodi, bude mit periodu 10s.
V tomto slova smyslu je tam, tedy v te druhe lodi….
….kde ja nejsem….
LukasM napsal(a):
….pomalejší čas.
V obou případech se při přechodu z klidu do pohybu rozdíl časů násobí faktorem gama (platí to pro události, které jsou v původní soustavě na stejném místě).
Nikde není problém.
Mozna chces rict, ze cas se zpomali v te druhe rakete z obou hledisek, tedy vzdycky z hlediska toho prvniho, co vzdycky pozoruje toho druheho.
Cili ten vzorec by mel podle toho a podle tebe byt 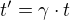 ??
??
Kdyz sem ted dam ten znamy priklad s dvojcaty, pak tedy:
Kdyz budem uvazovat, ze zpomaleni casu v soustave "v pohybu" znamena, ze kdyz se dvojce, ktere odletelo raketou rychlosti odpovidajici game=2, vrati po 100 letech uplynulych na Zemi, kde na nej bude cekat to druhe dvojce, bude tomu dvojceti, co se vrati, pouhych t'=50 let.
Neznamena to, ze hodiny toho dvojcete, co cestovalo, budou ukazovat t'=50 let, a tedy ciselne min?
Z tohoto pohledu to beru.
Protoze ono taky, to dvojce, co se vratilo, bude vedet, ze mu je t'=50 let, zatimco to dvojce na zemi bude vedet, ze jemu je t=100 let.
A proto, jestli jsem si ten vzorecek vymyslel nebo ne, nezda se byt jasne a logicke, ze to t' by se melo pocitat 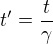 =100/2=50let????
=100/2=50let????
Kdybych tedy pouzil ten spravny vvzorec 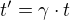 nevyslo by mi 100 x 2=200let ????
nevyslo by mi 100 x 2=200let ????
Jak bych tech 200 let potom vysvetlil? Musel bych je vydelit 4 abych dostal spravnou odpoved 50 let a kde bych ty 4 vzal?
Mozna to muzes tuhle ideu vysvetlit na tomhle priklade?
Je sice jasne, ze v te rakete "v pohybu" se perioda kyvadla zdvojnasobi z pohledu soustavy "v klidu", jenze to zdvojnasobeni znamena zpomaleni chodu casu dvakrat, coz by bylo vyjadreny pomoci 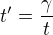 a ne
a ne 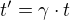 protoze snad ta pismena t a t' vyjadruji rychlost plynuti casu a ne delku periody kyvadla.
protoze snad ta pismena t a t' vyjadruji rychlost plynuti casu a ne delku periody kyvadla.
Skoro by se dalo rict, ze jelikoz ve vzorecku  gamou taky nasobime, davalo by to smysl ji tak pouzit i tady, ale nezda se to vychazet a prece je to hrozne zakladni problem, ale nenachazim pohled, ze ktereho by se to dalo nejak ospravedlnit.
gamou taky nasobime, davalo by to smysl ji tak pouzit i tady, ale nezda se to vychazet a prece je to hrozne zakladni problem, ale nenachazim pohled, ze ktereho by se to dalo nejak ospravedlnit.
Offline
#128 21. 06. 2018 02:44 — Editoval Zvedavec 4 (22. 06. 2018 04:15)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Relativita Soucasnosti
Cely ten cas se mi zda, ze jsem se nechal zbytecne zatahnout to kolotoce, ktery zkomplikoval co me je jednoduse jasne.
MichalAld napsal(a):
Jedinné vzorce které na relativitu současnosti potřebuješ je Lorentzova transformace.
kde
Vlastní relativita současnosti je situce kdy v nějaké souřadné soustavě nastanou dvě události ve stejný čas, ale v jiném místě.
Máme tedy událost A, o souřadnicícha událost B o souřadnicích
kde
No a teď nás zajímá, jaké budou souřadnice těchto událostí v jiné soustavě, jež se oproti té původní pohybuje rychlostí v. Protože nás zajímají jen časy, stačí když provedeme jen transformaci časových souřadnic. Takže:
Kdyz  bude ta 1ms a
bude ta 1ms a 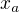 bude 600km, pak
bude 600km, pak  =0.
=0.
Kdyz  bude 1ms a
bude 1ms a  bude 0km, pak
bude 0km, pak 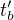 =1.154ms.
=1.154ms.
MichalAld napsal(a):
Je vidět, že "čárkované časy" už shodné nejsou, protože události měly různou x-ovou souřadnici. Můžeme spočítat rozdíl těch časů (v původní "nečárkované" soustavě si byly časy t_a a t_b rovny)
Pak 0-1.154ms=![kopírovat do textarea $\gamma (1ms-1ms-\frac{150 000\cdot [600-0]}{300 000^{2}})=-1.154ms$](/mathtex/2b/2b2abf4918ecb6588fb8e018e191217f.gif)
-1.154ms=-1.154ms
Coz uz bylo jasne od sameho zacatku!! (i kdyz tady jsem se puvodne splet v poctech a ted to opravvil po tom, co mne na to MichalAld upozornil v jednom z nasledujicich prispevku).
MichalAld napsal(a):
To je vztah pro relativitu současnosti. Nic víc a nic méně. Žádné "pozorovatele" ani "záblesky" nepotřebuješ, stačí jen pochopit, jak se v STR správně stanovují (nebo interpretují) časové a prostorové souřadnice.
Krome tohoto me neni jasne, co jineho se timto muze mit na mysli.
Offline
#129 21. 06. 2018 08:42 — Editoval Zvedavec 4 (21. 06. 2018 16:16)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Relativita Soucasnosti
Teprve ted me napada, ze snad o co vam jde je snad otazka, kdy ve vzdalenosti  ode mne se stane udalost A v case
ode mne se stane udalost A v case 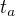 a potom jeste ve vzdalenosti
a potom jeste ve vzdalenosti 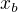 ode mne se stane jina, udalost B, v case
ode mne se stane jina, udalost B, v case 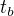 a ty muzou byt bud soucasny anebo soumistny anebo i oboji a ted nas zajima, co se s tema vzdalenostma a s tema casama udalosti stane v te druhe soustave, co bude "v pohybu", a jake tedy budou vysledne vzdalenosti tech udalosti od pozorovatele v te soustave, ktere tam budou oznaceny
a ty muzou byt bud soucasny anebo soumistny anebo i oboji a ted nas zajima, co se s tema vzdalenostma a s tema casama udalosti stane v te druhe soustave, co bude "v pohybu", a jake tedy budou vysledne vzdalenosti tech udalosti od pozorovatele v te soustave, ktere tam budou oznaceny  a
a  , a taky jake budou casy oznacene
, a taky jake budou casy oznacene 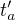 a
a 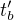 tech udalosti v te soustave "v pohybu" v tech mistech
tech udalosti v te soustave "v pohybu" v tech mistech  a
a  !!??
!!??
Jelikoz v tech dvou zminenych prikladech z wiki se udalost A nachazi primo v miste pozorovatele, pociita se jenom se vzdalenosti do udalosti B, kterou musi paprsek urazit. A tedy netreba rozdilu vzdalenosti (i kdyz se da rict, ze je to v podstate to same).
Jenze takovy priklad je mnohem jednoduzsi a uplne staci k tomu aby se udelal intuitivni obrazek o holem principu RS. O to mi vlastne jde a tenhle rozsireny priklad se to zda jen komplikovat.
Offline
#130 21. 06. 2018 17:04
Re: Relativita Soucasnosti
Zvedavec 4 napsal(a):
Cely ten cas se mi zda, ze jsem se nechal zbytecne zatahnout to kolotoce, ktery zkomplikoval co me je jednoduse jasne.
MichalAld napsal(a):
Jedinné vzorce které na relativitu současnosti potřebuješ je Lorentzova transformace.
kde
Vlastní relativita současnosti je situce kdy v nějaké souřadné soustavě nastanou dvě události ve stejný čas, ale v jiném místě.
Máme tedy událost A, o souřadnicícha událost B o souřadnicích
kde
No a teď nás zajímá, jaké budou souřadnice těchto událostí v jiné soustavě, jež se oproti té původní pohybuje rychlostí v. Protože nás zajímají jen časy, stačí když provedeme jen transformaci časových souřadnic. Takže:Kdyz
bude ta 1ms a
bude 600km, pak
=0.
Kdyzbude 1ms a
bude 0km, pak
=2ms.
No vidíš, propracováváme se kupředu. Už zbývá jen málo.
Škoda že jsi nenapsal, jakou jsi uvažoval tu vzájemnou rychlost soustav, ale z prvního předpokladu ( bude ta 1ms a
bude ta 1ms a 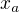 bude 600km, pak
bude 600km, pak  =0) plyne, že rychlost by měla být v=150 000 km/s (polovina rychlosti světla)
=0) plyne, že rychlost by měla být v=150 000 km/s (polovina rychlosti světla)
Z druhého předpokladu (Kdyz  bude 1ms a
bude 1ms a  bude 0km, pak
bude 0km, pak 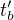 =2ms.) by pak ale pro tuhle ryhclost plynulo, že
=2ms.) by pak ale pro tuhle ryhclost plynulo, že 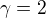 . Jenže to není pravda:
. Jenže to není pravda:
Takže platí, že 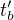 =1.155ms
=1.155ms
Offline
#131 21. 06. 2018 17:26
Re: Relativita Soucasnosti
Zvedavec 4 napsal(a):
Teprve ted me napada, ze snad o co vam jde je snad otazka, kdy ve vzdalenosti
ode mne se stane udalost A v case
a potom jeste ve vzdalenosti
ode mne se stane jina, udalost B, v case
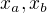 nejsou vzdálenosti, jsou to souřadnice (tedy řekněme vzdálenosti od počátku zvolené souřadné soustavy, nemusí to být nutně vzdálenosti od tebe).
nejsou vzdálenosti, jsou to souřadnice (tedy řekněme vzdálenosti od počátku zvolené souřadné soustavy, nemusí to být nutně vzdálenosti od tebe).
Zvedavec 4 napsal(a):
a ty muzou byt bud soucasny anebo soumistny anebo i oboji a ted nas zajima, co se s tema vzdalenostma a s tema casama udalosti stane v te druhe soustave, co bude "v pohybu", a jake tedy budou vysledne vzdalenosti tech udalosti od pozorovatele v te soustave, ktere tam budou oznaceny
a
, a taky jake budou casy oznacene
a
tech udalosti v te soustave "v pohybu" v tech mistech
a
!!??
No ano, pokud tedy nahradíme tvé "vzdálenost od pozorovatele" výrazem "vzdáleností od počátku".
Zvedavec 4 napsal(a):
Jelikoz v tech dvou zminenych prikladech z wiki se udalost A nachazi primo v miste pozorovatele,
Né, nacházela se v počátku souřadného systému.
Zvedavec 4 napsal(a):
pociita se jenom se vzdalenosti do udalosti B, kterou musi paprsek urazit. A tedy netreba rozdilu vzdalenosti (i kdyz se da rict, ze je to v podstate to same).
Nevím, o jakém paprsku mluvíš, ale určitě je to špatně...
Zvedavec 4 napsal(a):
Jenze takovy priklad je mnohem jednoduzsi a uplne staci k tomu aby se udelal intuitivni obrazek o holem principu RS. O to mi vlastne jde a tenhle rozsireny priklad se to zda jen komplikovat.
Komplikuješ to jen ty svými "pozorovateli" a "paprsky". Jinak je to pořád to samé. A ano, je vhodné si zvolit jednu událost v poloze nula a čase nula, ušetří nám to nějaké to počítání. Jenže to by taky musel někdo pochopit, že je to záměr...Jinak máš ale pravdu, je to "v podstatě" to samé.
Offline
#132 21. 06. 2018 17:33
Re: Relativita Soucasnosti
Zvedavec 4 napsal(a):
Kdyz budem uvazovat, ze zpomaleni casu v soustave "v pohybu" znamena, ze kdyz se dvojce, ktere odletelo raketou rychlosti odpovidajici game=2, vrati po 100 letech uplynulych na Zemi, kde na nej bude cekat to druhe dvojce, bude tomu dvojceti, co se vrati, pouhych t'=50 let.
Tohle je ale ovšem trochu jiný problém, který přesahuje speciální teorii relativity.
To dvojče co odletělo a zase se vrátilo, se alespoň část cesty muselo pohybovat jinak než konstantní rychlostí, jinak by se nemohlo vrátit. A když se něco pohybuje jinak než konstantní rychlostí, nemůžeme použít jen speciální relativitu, musíme použít i něco z té obecné teorie relativity.
Takže pokud nepochopíš základy, nemá moc smysl se pouštět do složitějších věcí.
Offline
#133 22. 06. 2018 04:36
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Relativita Soucasnosti
MichalAld napsal(a):
Zvedavec 4 napsal(a):
Kdyz
bude 1ms a
bude 0km, pak
=2ms.
No vidíš, propracováváme se kupředu. Už zbývá jen málo.
Škoda že jsi nenapsal, jakou jsi uvažoval tu vzájemnou rychlost soustav, ale z prvního předpokladu (bude ta 1ms a
bude 600km, pak
=0) plyne, že rychlost by měla být v=150 000 km/s (polovina rychlosti světla)
Z druhého předpokladu (Kdyzbude 1ms a
bude 0km, pak
=2ms.) by pak ale pro tuhle ryhclost plynulo, že
. Jenže to není pravda:
Takže platí, že=1.155ms
Vlastne jsem tu rychlost 150 000km/s tam udanou mel, a to v tom zaverecnem velkem vzorci, ale nejak sis toho nevsim.
Diky za upozorneni. Pohravam si tady s prikladama z STR dost dlouhho a tudiz vim dobre, ze  150 000km/s je 1.154 (gama=2 je samozrejme pro rychhlost v=259 807.621 1km/s) a proto to byla jenom nepozornost z me strany. Dodatecne jsem to opravil.
150 000km/s je 1.154 (gama=2 je samozrejme pro rychhlost v=259 807.621 1km/s) a proto to byla jenom nepozornost z me strany. Dodatecne jsem to opravil.
Uz jsem sem daval stejny vypocet v okne 54 a tam jsem byl pozornejsi a tudiz se nesplet.
Offline
#134 22. 06. 2018 05:47 — Editoval Zvedavec 4 (22. 06. 2018 06:03)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Relativita Soucasnosti
MichalAld napsal(a):
Zvedavec 4 napsal(a):
Teprve ted me napada, ze snad o co vam jde je snad otazka, kdy ve vzdalenosti
ode mne se stane udalost A v case
a potom jeste ve vzdalenosti
ode mne se stane jina, udalost B, v case
MichalAld napsal(a):
nejsou vzdálenosti, jsou to souřadnice (tedy řekněme vzdálenosti od počátku zvolené souřadné soustavy, nemusí to být nutně vzdálenosti od tebe).
Nemuzes me takhle hned chytat za slovo. Presne to, co rikas, jesm mel na mysli, i kdyz mas pravdu, protoze jsem se nevyjadril presne. Bral jsem to, ze kdyz se nekde v
a v
stanou dve udalosti, ja budu umisteny na zacatku soustavy, tedy v miste, ke kteremu se to vztahuje a nejsou tedy tim ta
a
zaroven vzdalenosti tech udalosti ode mne?
Temhle detajlum, i kdyz jsou dulezite, moc pozornosti nedavam, protoze mi jde celkove trochu o neco jineho, nez dosazovat do danych vzorecku. Jsou detajly, co mne zajimaji a detajly, co mne nezajimaji. Ale mel jsem v planu si postupne i v tomhle udelat jasno az vstrebam, co mne hlavne zajima. Priste se polepsim.Zvedavec 4 napsal(a):
a ty muzou byt bud soucasny anebo soumistny anebo i oboji a ted nas zajima, co se s tema vzdalenostma a s tema casama udalosti stane v te druhe soustave, co bude "v pohybu", a jake tedy budou vysledne vzdalenosti tech udalosti od pozorovatele v te soustave, ktere tam budou oznaceny
a
, a taky jake budou casy oznacene
a
tech udalosti v te soustave "v pohybu" v tech mistech
a
!!??
MichalAld napsal(a):
No ano, pokud tedy nahradíme tvé "vzdálenost od pozorovatele" výrazem "vzdáleností od počátku".
Beru to na vedomi, protoze to je definitivne presnejsi.
Nesoustredil jsem se zrovna na detajly o sourednicich, protoze verim, ze zaklady o nich potrebne k STR mi jsou celkem jasne.Zvedavec 4 napsal(a):
Jelikoz v tech dvou zminenych prikladech z wiki se udalost A nachazi primo v miste pozorovatele,
MichalAld napsal(a):
Né, nacházela se v počátku souřadného systému.
Ano, tak jsem to mel vyjadrit.
Zvedavec 4 napsal(a):
pociita se jenom se vzdalenosti do udalosti B, kterou musi paprsek urazit. A tedy netreba rozdilu vzdalenosti (i kdyz se da rict, ze je to v podstate to same).
MichalAld napsal(a):
Nevím, o jakém paprsku mluvíš, ale určitě je to špatně…
No opakuju jen tady ten prvni priklad z wiki o zablesku v B, co je puvodne spatren v bode A o 1ms pozdeji nez zablesk, co se stane v tom bode A, ktery je 600km vzdalen od B a umisten v pocatku sveho souradneho systemu, a ktere (ty dva zablesky) se stanou soucasnymi pro pozorovatele umisteneho v pocatku souradneho systemu soustavy "v pohybu", kdyz pocatek souradneho systemu soustavy "v pohybu" se pri letu v=150 000km/s bude kryt s pocatkem souradneho systemu soustavy "v klidu", tedy presne v miste zablesku A.
Zvedavec 4 napsal(a):
Jenze takovy priklad je mnohem jednoduzsi a uplne staci k tomu aby se udelal intuitivni obrazek o holem principu RS. O to mi vlastne jde a tenhle rozsireny priklad se to zda jen komplikovat.
MichalAld napsal(a):
Komplikuješ to jen ty svými "pozorovateli" a "paprsky". Jinak je to pořád to samé. A ano, je vhodné si zvolit jednu událost v poloze nula a čase nula, ušetří nám to nějaké to počítání. Jenže to by taky musel někdo pochopit, že je to záměr...Jinak máš ale pravdu, je to "v podstatě" to samé.
Soucasne me to pripada o dost nazornejsi, a tedy jednoduzsi, pouzivat pozorovatele a paprsky, i kdyz si dovedu predstavit, ze jak se jednou tyhle priklady vstrebaji, muze to byt lepsi bez nich.
Jenze jak rikam, muj cil ze zacatku byl pochopit, co se vlastne pri tech vzajemnych pohybech soustav deje a proc, samosebou pokud mozno, a ne jenom dosazovani do predlozenych vzorcu, i kdyz ani tomu by se nemelo vyhybat, a proto moc neprotestuju, kdyz mne k tomu forum nabada.
Offline
#135 22. 06. 2018 06:49
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Relativita Soucasnosti
MichalAld napsal(a):
Zvedavec 4 napsal(a):
Kdyz budem uvazovat, ze zpomaleni casu v soustave "v pohybu" znamena, ze kdyz se dvojce, ktere odletelo raketou rychlosti odpovidajici game=2, vrati po 100 letech uplynulych na Zemi, kde na nej bude cekat to druhe dvojce, bude tomu dvojceti, co se vrati, pouhych t'=50 let.
Tohle je ale ovšem trochu jiný problém, který přesahuje speciální teorii relativity.
To dvojče co odletělo a zase se vrátilo, se alespoň část cesty muselo pohybovat jinak než konstantní rychlostí, jinak by se nemohlo vrátit. A když se něco pohybuje jinak než konstantní rychlostí, nemůžeme použít jen speciální relativitu, musíme použít i něco z té obecné teorie relativity.
Takže pokud nepochopíš základy, nemá moc smysl se pouštět do složitějších věcí.
I tohle mi je jasne. Aniz bych se kdy chtel poustet do OTR, stejne se o ni obcas zminuji v textech o STR.
A tak treba vim, ze vlastne to zpomaleni chodu casu neni snad ani tak vysledkem pohybu, se domnivaj, jako zrychleni, kterym se toho pohybu musi dosahnout.
Protoze i na te jedne strance wiki, na kterou jsem sem uz odkaz poslal, ho taky rozebiraji, ale muzu rict, ze mne nezajima dost na to abych se snazil prodrat tema diagramama, kteryma to osvetlujou.
Ale, coby dobry priklad toho, na co jsem se snazil privezt pozornost, jsem ho pouzil.
A to sice na nejaky nejprazakladnejsi vzorecek pro spocitani t', tedy, jak se udava, 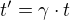 . Tohle je jedna z veci, v kterou jsem doufal se tady nejak vysvetli.
. Tohle je jedna z veci, v kterou jsem doufal se tady nejak vysvetli.
Po poznani par zakladu o STR se musi prece dojit k zaveru, ze kdyz se cas, ktery se znaci t', a ktery ma bezet v soustave "v pohybu", ma zpomalit at uz dvakrat anebo na polovinu, pri ubehlych t=10s meho casu v soustave "v klidu", nejjednoduzsim zpusobem, jak toho docilit se zda vydelenim deseti dvema, tedy 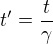 = 5s.
= 5s.
Hledal jsem to na wiki a nikde nenasel ale vim, ze ho celou tu dobu mam v povedomi a je tedy pravdepodobny, ze jsem si ho vymyslel, protoze je tak ocividny.
Nemuzu tvrdit, ze je spravny a ten prvni neni.
Taky mi je jasne, ze uz sama TR je postavena na urcitych uhlech pohledu na veci, co se dejou pri velkych rychlostech, protoze se vymykaji normalni uvaze a zkusenostem. Takze i ten vztah 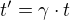 , kdyz je tedy spravny, musi mit vysvetleni akorat nemuzu prijit na to, jak spatrit jeho logiku. Protoze pri vynasobeni vyjde 20s a ne 5s.
, kdyz je tedy spravny, musi mit vysvetleni akorat nemuzu prijit na to, jak spatrit jeho logiku. Protoze pri vynasobeni vyjde 20s a ne 5s.
Dobre je to naznacene pomoci tech period kyvadel, ale kdyz ten druhy vzorec, tedy 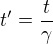 je o tolik jasnejsi, v jakem smyslu tedy neni spravny? Bude to nejspis neco matematickeho.
je o tolik jasnejsi, v jakem smyslu tedy neni spravny? Bude to nejspis neco matematickeho.
Offline
#136 22. 06. 2018 07:25
Re: Relativita Soucasnosti
↑ Zvedavec 4:
Proboha, pomalejsi cas snad znamena, ze doba mezi zvolenymi udalostmi je DELSI nez puvodne. Takze pokud ho oznacim  v soustave v klidu a
v soustave v klidu a  v soustave v pohybu, tak
v soustave v pohybu, tak  bude vetsi (pri pohledu z pohybu dej trva dele). V prispevku #127 pises
bude vetsi (pri pohledu z pohybu dej trva dele). V prispevku #127 pises
protoze snad ta pismena t a t' vyjadruji rychlost chodu casu a ne delku periody kyvadla
Samozrejme, ze je to perioda kyvadla. Jak to po 130 prispevcich muze byt nejasne?
Ostatni body nebudu komentovat, na to nemam silu. Jenom ti chci podekovat za vypraveni o nedostatcich matematiky - pohled cloveka, ktery tu uz pul roku odmita upravovat zlomky, je v tomto nesmirne cenny a inspirujici. Matematika ti samozrejme nerekne, jak se ma co spocitat, stejne jako ti auto nerekne, kam mas jet na dovolenou. Navod jak to spocitat nam dava prave STR. Ze si to ty vymyslis po svem, to je tvuj problem a matematika za to opravdu nemuze.
Offline
#137 22. 06. 2018 15:27
Re: Relativita Soucasnosti
Zvedavec 4 napsal(a):
No opakuju jen tady ten prvni priklad z wiki o zablesku v B, co je puvodne spatren v bode A o 1ms pozdeji nez zablesk, co se stane v tom bode A, ktery je 600km vzdalen od B a umisten v pocatku sveho souradneho systemu, a ktere (ty dva zablesky) se stanou soucasnymi pro pozorovatele umisteneho v pocatku souradneho systemu soustavy "v pohybu", kdyz pocatek souradneho systemu soustavy "v pohybu" se pri letu v=150 000km/s bude kryt s pocatkem souradneho systemu soustavy "v klidu", tedy presne v miste zablesku A.
Asi jsem hloupej, ale tohle prostě nechápu. Nemohl bys to napsat tak, aby to dávalo smysl ?
Zvedavec 4 napsal(a):
Jenze jak rikam, muj cil ze zacatku byl pochopit, co se vlastne pri tech vzajemnych pohybech soustav deje a proc,
No já vím, ale to je právě ten problém, že se snažíš pochopit PROČ to tak je, a že si myslíš, že umísťováním nějakých človíčků do souřadných soustav a přidáváním nějakých záblesků a paprsků vymyslíš, proč to tak je.
Jenže nevymyslíš, nemá to žádné hlubší vysvětlení (jako ostatně všechny fundamentální přírodní zákony). Neexistuje žádné vysvětlení, proč se tak svět chová. Můžeme jenom řešit jak se (přesně) chová, ale né PROČ.
Tudíš všechny tvé snahy o "intuitivní pochopení" PROČ to tak je jsou předem odsouzeny k nezdaru...
Offline
#138 22. 06. 2018 15:44 — Editoval MichalAld (22. 06. 2018 15:46)
Re: Relativita Soucasnosti
Zvedavec 4 napsal(a):
to sice na nejaky nejprazakladnejsi vzorecek pro spocitani t', tedy, jak se udava,
. Tohle je jedna z veci, v kterou jsem doufal se tady nejak vysvetli.
Po poznani par zakladu o STR se musi prece dojit k zaveru, ze kdyz se cas, ktery se znaci t', a ktery ma bezet v soustave "v pohybu", ma zpomalit at uz dvakrat anebo na polovinu, pri ubehlych t=10s meho casu v soustave "v klidu", nejjednoduzsim zpusobem, jak toho docilit se zda vydelenim deseti dvema, tedy= 5s.
Víš, ty na to pořád koukáš takovým poloklasickým pohledem. Sice jako nějak bereš, že v každé soustavě běží čas jinak rychle, ale pořád ještě nechápeš, že tohle není všechno. Že čas ještě nějak závisí i na poloze.
Samotný časový údaj nemá smysl uvádět, pokud k němu není i prostorová souřadnice.
Takže kdybychom chtěli být přesní, tak tvůj první vzorec 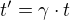 je speciální případ obecného vztahu
je speciální případ obecného vztahu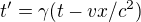
za předpokladu, že x = 0. To je důležitá věc, kterou sice nemusíme vždy psát, ale musíme si ji vždy uvědomit.
Jenže to ty neděláš.
No a pak je další věc, že k tomu t' musí existovat také x', spočtené dle toho druhého vzahu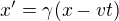
A zde je vidět, že x' už nulové nebude, nebude ani konstantní, bude to  .
.
Pokud tedy do počítáku "nečárkované" soustavy umístíme blikač s periodou 1s, bude interval záblesků v "čárkované" soustavě delší, ale zároveň bude také každý záblesk zaznamenán na jiném místě.
Pokud bychom chtěli použít opačný vztah 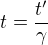 , museli bychom narafičit dost nepravděpodobnou inverzní situaci, tj v "čárkované" soustavě by nebyl jeden blikač, ale byla by jich celá řada, a krom toho, že by blikaly s intervalem t', museli by se také nacházet každý v jiném místě, s roztečemi x'. Což jistě uznáš i ty, že je to dost nepravděpodobná situace, která se těžko někdy někde vyskytne, takže proto se s takovýmto vztahem
, museli bychom narafičit dost nepravděpodobnou inverzní situaci, tj v "čárkované" soustavě by nebyl jeden blikač, ale byla by jich celá řada, a krom toho, že by blikaly s intervalem t', museli by se také nacházet každý v jiném místě, s roztečemi x'. Což jistě uznáš i ty, že je to dost nepravděpodobná situace, která se těžko někdy někde vyskytne, takže proto se s takovýmto vztahem 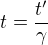 nikde nesetkáš.
nikde nesetkáš.
Ale tvá představa, že existuje něco jako "rychlost běhu času" v "klidové" a "pohybující se" soustavě, to je úplně špatně. To by byl opravdu paradox, protože těžko může běžet čas v jedné soustavě rychleji než ve druhé a zároveň ve druhé rychleji než v té první.
Trik je právě v tom, že v jedné soustavě je ten časový generágor pořád na stejném místě, zatímco v té druhé detekujeme jeho tiky pokaždé na jiném místě.
Když dáme časový generátor do druhé soustavy, budou zase jeho tiky delší v té první - protože to bude pak v té první soustavě, že nebudou tiky detekovány ve stejném místě.
Takže ještě jednou opakuji - řešit jen čas je NESMYSL. Vždy se musí řešit i poloha. Neexistuje něco jako obecná rychlost plynutí času.
A to je to co pořád opakuji - tvá představa pozorovatele v počátku souřadnic je špatná. Musíš mít pozorovatele v každém bodě soustavy - a každý musí mít své hodinky k měření času. Jinak se z toho nevymotáš, z matematikou nebo bez ní.
Offline
#139 24. 06. 2018 18:14 — Editoval Zvedavec 4 (24. 06. 2018 18:21)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Relativita Soucasnosti
MichalAld napsal(a):
Zvedavec 4 napsal(a):
No opakuju jen tady ten prvni priklad z wiki o zablesku v B, co je puvodne spatren v bode A o 1ms pozdeji nez zablesk, co se stane v tom bode A, ktery je 600km vzdalen od B a umisten v pocatku sveho souradneho systemu, a ktere (ty dva zablesky) se stanou soucasnymi pro pozorovatele umisteneho v pocatku souradneho systemu soustavy "v pohybu", kdyz pocatek souradneho systemu soustavy "v pohybu" se pri letu v=150 000km/s bude kryt s pocatkem souradneho systemu soustavy "v klidu", tedy presne v miste zablesku A.
Asi jsem hloupej, ale tohle prostě nechápu. Nemohl bys to napsat tak, aby to dávalo smysl ?
Hrozne jsem spechal to dopsat a poslat a videl jsem, jak se do toho zamotavam vic a vic, ale nechtel jsem to prepisovat. Je to prece ale ten priklad, kterym jsem zacal toto vlakno, a tedy:
Pozorovatel v bode A zaznamena udalost, tedy zablesk svetla, primo vedle sebe. Po 1ms zaznamena udalost B, tedy taky zablesk svetla, co k nemu dorazil z bodu B 600km vzdalenem od neho, tedy od bodu A. Jakou rychlosti bude muset letet raketa aby v okamziku, co se pocatek jejiho souradneho systemu kryje s pocatekem souradneho systemu soustavy "v klidu" toho pozorovatele, kosmonaut v te rakete soudil ty dva zablesky coby soucasne?
Prestoze jste mne s Lukasem na samem pocatku tohoto vlakna odrazovali tim, ze neni pripustne uvazovat o udalosti 600km vzdalene, pokousim se to zformulovat po vasem, a tedy:
Udalost na pocatku souradneho systemu soustavy "v pohybu" B se stane o 1ms po udalosti soustavy "v klidu" A (podle soustavy A), co se taky stala v pocatku jejiho souradneho systemu. Pocatky tech dvou souradnych systemu jsou od sebe vzdaleny 600km v okamziku, kdy se stane udalost B (taky podle soustavy A). Jestlize se v soustave "v klidu" ty dve udalosti stanou 1ms po sebe, jak rychle se bude muset soustava B, tedy ta "v pohybu", premistovat casoprostorem aby se v ni ty dve udalosti staly soucasne?
Jestli se tohle da vubec takhle popsat, je to poradne narocny. Nejsem si ted jisty s temi pocatky soustav, ale zase nemam cas to prepracovat. Pozdeji.
Mozna proto, ze jsem si zvyk o tom uvazovat intuitivne, to prvni zadani je jasnejsi, pokud se tomu chce porozumnet z toho intuitivniho pohledu (s trochou matematiky). Mozna proto, ze se jedna o zablesky a tedy jasne vypliva jak se to asi vyviji.
Offline
#140 24. 06. 2018 18:56 — Editoval MichalAld (24. 06. 2018 23:14)
Re: Relativita Soucasnosti
Zvedavec 4 napsal(a):
Udalost na pocatku souradneho systemu soustavy "v pohybu" B se stane o 1ms po udalosti soustavy "v klidu" A (podle soustavy A), co se taky stala v pocatku jejiho souradneho systemu. Pocatky tech dvou souradnych systemu jsou od sebe vzdaleny 600km v okamziku, kdy se stane udalost B (taky podle soustavy A). Jestlize se v soustave "v klidu" ty dve udalosti stanou 1ms po sebe, jak rychle se bude muset soustava B, tedy ta "v pohybu", premistovat casoprostorem aby se v ni ty dve udalosti staly soucasne?
Né, tohle opravdu není dobře. Navíc to ani nedává smysl.
Události musíme popisovat všechny v jedné a té samé soustavě (jedno jaké), nemůžeme ale brát jednu událost z jedné soustavy a druhou z druhé.
Správně je to takto:
1) Na volbě počátků soustav vůbec nezáleží. Lze je umístit kamkoliv, a v tomto případě se jimi nemusíme vůbec zabývat. Ta podmínka "... aby v okamziku, co se pocatek jejiho souradneho systemu kryje s pocatekem souradneho systemu soustavy "v klidu" toho pozorovatele..." je úplně zbytečná.
2) Ve skutečnosti tam máme tři události:
K - zaznamenáme záblesk v bodě A (v nějakém čase t)
L - zaznamenáme záblesk v bodě B (musí k ní dojít o 1ms dříve než k události K)
M - záblesk zaznamenaný v bodě B dorazí i do bodu A.
(záblesk se pohybuje rychlostí světla, a vzdálenost bodů je 600km, takže tam dorazí za 2ms,
událost M tedy nastane o 1 ms po události K).
Tohle všechno je popsáno v rámci stejné soustavy (té "klidové", spojené s body A a B). Schválně jsem dal událostem jiná označení než těm bodům, aby bylo jasné, že je to něco (úplně) jiného.
No a my se ptáme, jak rychle se musí pohybovat nějaká raketa, aby v soustavě s ní spojené byly události K a L současné. To se dá celkem snadno spočítat...
Událost M nemá na "relativitu současnosti" událostí K a L vůbec žádný vliv, a vůbec by v příkladě být nemusela. Stejně jako ten požadavek na počátky souřadných soustav. Celé to jenom zamotává.
Takže - dokážeš se s tím srovnat i bez události M ? Bez toho, aby mezi B a A letěl nějaký světelný paprsek ?
Pokud né, je to dál jen ztráta času...
Offline
#141 25. 06. 2018 04:39 — Editoval Zvedavec 4 (25. 06. 2018 05:57)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Relativita Soucasnosti
MichalAld napsal(a):
2) Ve skutečnosti tam máme tři události:
K - zaznamenáme záblesk v bodě A (v nějakém čase t)
L - zaznamenáme záblesk v bodě B (musí k ní dojít o 1ms dříve než k události K)
M - záblesk zaznamenaný v bodě B dorazí i do bodu A.
(záblesk se pohybuje rychlostí světla, a vzdálenost bodů je 600km, takže tam dorazí za 2ms,
událost M tedy nastane o 1 ms po události K).
Tohle všechno je popsáno v rámci stejné soustavy (té "klidové", spojené s body A a B). Schválně jsem dal událostem jiná označení než těm bodům, aby bylo jasné, že je to něco (úplně) jiného.
No a my se ptáme, jak rychle se musí pohybovat nějaká raketa, aby v soustavě s ní spojené byly události K a L současné. To se dá celkem snadno spočítat...
Událost M nemá na "relativitu současnosti" událostí K a L vůbec žádný vliv, a vůbec by v příkladě být nemusela. Stejně jako ten požadavek na počátky souřadných soustav. Celé to jenom zamotává.
Takže - dokážeš se s tím srovnat i bez události M ? Bez toho, aby mezi B a A letěl nějaký světelný paprsek ?
Pokud né, je to dál jen ztráta času...
Protoze jsem napsal, ze to neni dobre, doufal jsem, ze nikdo neodpovi, chtel jsem to opravit pozdeji, protoze neexistuje moznost, jak to smazat a nechtelo se mi to mazat castecne a nejak to upravovat aby to davalo alespon nejaky smysl. Nemel jsem cas. Chyba tedy byla, ze jsem se do toho vubec poustel.
Odpoved na tvou otazku je zcela jednoducha.
Ty prece jenom prohazujes to, co jsem popsal v tom mem prvnim zadani, kdy tedy tvoje udalost M ve tve verzi nema na RS zadny vliv, protoze uz na ni nedojde, jelikoz beres coby prvni tu udalost B co se ve skutecnosti stane driv, kdezto v mem zadani se udalost A bere coby prvni nebot jakoby se ona stala driv. A proto v mem prvnim zadani by tvoje udalost L nemela zadny vliv. Je to jasne.
A ten zbytek je to same, co moje. Na to jsem se neptal.
Offline
#142 25. 06. 2018 05:52 — Editoval Zvedavec 4 (25. 06. 2018 06:19)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Relativita Soucasnosti
Slo mi prece o to ten priklad upravit tak aby tam zablesky nehraly zadnou roli podle toho jak rikas, ze zablesky a pozorovatele nepotrebujem. Takze to jsou jenom hole udalosti. Zda se, ze tenhle priklad tak upravit nejde.
Offline
#143 25. 06. 2018 16:41 — Editoval Zvedavec 4 (25. 06. 2018 16:46)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Relativita Soucasnosti
Budu muset tohle tve okno (#138) "rozebrat" po trochach.
Jelikoz ani tady ani jinde jsem se nesetkal s vysvetlenim vzorecku  , po dlouhe dobe uvazovani jsem si s jeho vysvetlenim musel prijit sam. Zminil jsem se o tom v mem vlakne "Vypocet t'", ale protoze to nikdo neokomentoval, muze byt z hlediska pouzivane a vzite matematiky STR a chapani o cem je nedulezity nebo dokonce chybny atd. Nicmene pro mne to, s cim jsem prisel, plne vysvetluje, co se kolem neho deje.
, po dlouhe dobe uvazovani jsem si s jeho vysvetlenim musel prijit sam. Zminil jsem se o tom v mem vlakne "Vypocet t'", ale protoze to nikdo neokomentoval, muze byt z hlediska pouzivane a vzite matematiky STR a chapani o cem je nedulezity nebo dokonce chybny atd. Nicmene pro mne to, s cim jsem prisel, plne vysvetluje, co se kolem neho deje.
MichalAld napsal(a):
Víš, ty na to pořád koukáš takovým poloklasickým pohledem. Sice jako nějak bereš, že v každé soustavě běží čas jinak rychle, ale pořád ještě nechápeš, že tohle není všechno. Že čas ještě nějak závisí i na poloze.
Samotný časový údaj nemá smysl uvádět, pokud k němu není i prostorová souřadnice.
Takže kdybychom chtěli být přesní, tak tvůj první vzorecje speciální případ obecného vztahu
za předpokladu, že x = 0. To je důležitá věc, kterou sice nemusíme vždy psát, ale musíme si ji vždy uvědomit.
Jenže to ty neděláš.
Tady o tom jsem se zminoval a dotazoval se na to nekolikrat prave v tom vlakne "Vypocet t'", ktery je dukazem, ze jsem si alespon neceho z toho, o cem se v tomhle okne zminujes, vedom. Napriklad v okne #7:
Zvedavec 4 napsal(a):
Hodnoty v tomhle priklade jsou zavadejici v tom, ze ubehly cas rakety v jeji soustave, tedy 500 vterin v dobe udalosti, je ciselne totozny s casem souradnym t', ve kterem se ta udalost stane na jeji casove souradnici, tedy taky 500 vterin.
Co jsem tim myslel je prave pripad, kdy x'=0.
Co me porad nehraje je presne tohleto: pro udaje v=259 807.621km/s; t=1s; x=259 807.621km; gama=2
Jestlize jeden je specialnim pripadem druheho, proc jsou vysledky navzajem protichudne mi neni jasne.
x'=0; a 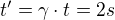 ale
ale  Tak v cem to tady vezi? Tohle me mate. Kde delam nejakou zakladni chybu? A kde a jak by tedy vysledek spocitany pomoci tohoto vztahu
Tak v cem to tady vezi? Tohle me mate. Kde delam nejakou zakladni chybu? A kde a jak by tedy vysledek spocitany pomoci tohoto vztahu 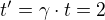 mohl byt pouzity/se pouzije? Tady bych potreboval konkretni pripad.
mohl byt pouzity/se pouzije? Tady bych potreboval konkretni pripad.
Trochu niz se pak zminujjes o slozitem pripade, kdyby se pouzil ten druhy vztah, tedy 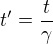 a beru to plne na vedomi a asi nepotrebuju vedet detajly, protoze to vypada slozity. Tak jen mozna ukazka, kdy a jak by se pouzilo tohodle protichudneho vysledku by mohla pomoct.
a beru to plne na vedomi a asi nepotrebuju vedet detajly, protoze to vypada slozity. Tak jen mozna ukazka, kdy a jak by se pouzilo tohodle protichudneho vysledku by mohla pomoct.
Offline
#144 25. 06. 2018 21:42
Re: Relativita Soucasnosti
Zvedavec 4 napsal(a):
Ty prece jenom prohazujes to, co jsem popsal v tom mem prvnim zadani, kdy tedy tvoje udalost M ve tve verzi nema na RS zadny vliv, protoze uz na ni nedojde, jelikoz beres coby prvni tu udalost B co se ve skutecnosti stane driv, kdezto v mem zadani se udalost A bere coby prvni nebot jakoby se ona stala driv. A proto v mem prvnim zadani by tvoje udalost L nemela zadny vliv. Je to jasne.
To si nemůžeš zvolit, která událost se "jakoby stane dřív". Dříve se stane to, co má nižší hodnotu časové souřadnice.
Nejprve dojde k události L (v bodě B)
Potom dojde k události K (v bodě A)
Naposledy dojde k události M (v bodě A)
Není žádný důvod, proč by k události M nemělo dojít.
Žádná "alternativní" možnost není. Žádné "v mém zadání je to jakoby jinak" neplatí. Zadání máme to samé.
Takže všechno to, co tady říkáš, je nesmysl.
Offline
#145 25. 06. 2018 21:46 — Editoval MichalAld (25. 06. 2018 21:46)
Re: Relativita Soucasnosti
Zvedavec 4 napsal(a):
MichalAld napsal(a):
Víš, ty na to pořád koukáš takovým poloklasickým pohledem. Sice jako nějak bereš, že v každé soustavě běží čas jinak rychle, ale pořád ještě nechápeš, že tohle není všechno. Že čas ještě nějak závisí i na poloze.
Samotný časový údaj nemá smysl uvádět, pokud k němu není i prostorová souřadnice.
Takže kdybychom chtěli být přesní, tak tvůj první vzorecje speciální případ obecného vztahu
za předpokladu, že x = 0. To je důležitá věc, kterou sice nemusíme vždy psát, ale musíme si ji vždy uvědomit.
Jenže to ty neděláš.Tady o tom jsem se zminoval a dotazoval se na to nekolikrat prave v tom vlakne "Vypocet t'", ktery je dukazem, ze jsem si alespon neceho z toho, o cem se v tomhle okne zminujes, vedom. Napriklad v okne #7:
Zvedavec 4 napsal(a):
Hodnoty v tomhle priklade jsou zavadejici v tom, ze ubehly cas rakety v jeji soustave, tedy 500 vterin v dobe udalosti, je ciselne totozny s casem souradnym t', ve kterem se ta udalost stane na jeji casove souradnici, tedy taky 500 vterin.
Co jsem tim myslel je prave pripad, kdy x'=0.
Co me porad nehraje je presne tohleto: pro udaje v=259 807.621km/s; t=1s; x=259 807.621km; gama=2
Jestlize jeden je specialnim pripadem druheho, proc jsou vysledky navzajem protichudne mi neni jasne.
x'=0; aale
Tak v cem to tady vezi? Tohle me mate. Kde delam nejakou zakladni chybu?
Co k tomu dodat? Zjevně asi x=0 a x'=0 neznamená totéž...
Offline
#146 26. 06. 2018 07:33 — Editoval Zvedavec 4 (26. 06. 2018 17:04)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Relativita Soucasnosti
MichalAld napsal(a):
Zvedavec 4 napsal(a):
MichalAld napsal(a):
za předpokladu, že x = 0. To je důležitá věc, kterou sice nemusíme vždy psát, ale musíme si ji vždy uvědomit.
Jenže to ty neděláš.Co jsem tim myslel je prave pripad, kdy x'=0.
x'=0; aale
Tak v cem to tady vezi? Tohle me mate. Kde delam nejakou zakladni chybu?
Co k tomu dodat? Zjevně asi x=0 a x'=0 neznamená totéž...
Za nejake 2 hod po tom, co jsem to napsal, jsem si tu chybu uvedomil, ale k pocitaci jsem se dostal az ted. Ono totiz x'=0 je taky, v jistym slova smyslu, specialni pripad, ne? I kdyz asi trochu min.
Offline
#147 26. 06. 2018 08:13 — Editoval Zvedavec 4 (26. 06. 2018 16:55)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Relativita Soucasnosti
MichalAld napsal(a):
Zvedavec 4 napsal(a):
Ty prece jenom prohazujes to, co jsem popsal v tom mem prvnim zadani, kdy tedy tvoje udalost M ve tve verzi nema na RS zadny vliv, protoze uz na ni nedojde, jelikoz beres coby prvni tu udalost B co se ve skutecnosti stane driv, kdezto v mem zadani se udalost A bere coby prvni nebot jakoby se ona stala driv. A proto v mem prvnim zadani by tvoje udalost L nemela zadny vliv. Je to jasne.
To si nemůžeš zvolit, která událost se "jakoby stane dřív". Dříve se stane to, co má nižší hodnotu časové souřadnice.
Nejprve dojde k události L (v bodě B)
Potom dojde k události K (v bodě A)
Naposledy dojde k události M (v bodě A)
Není žádný důvod, proč by k události M nemělo dojít.
Celkem to chapu, ty tady ale rozsirujes ten uz prodlouzeny vzorec na 3 udalosti. Ja to ciste vice mene opakuju po wiki, kde tedy povazujou jen ty dve udalosti, ktere maji vliv na priklad, kterym jenom chteji znazornit princip RS. Vim, ze to vis, ale bere se to, v mem porozumeni, z hlediska pozorovatele v udalosti/bode A, kdy ho prece nebude zajimat, ze se ten zablesk v B stal ve skutecnosti driv. Jeho zajima jen to, co zaznamena a to je prvni zaznamena zablesk z A, tedy tvoje K a potom zaznamena zablesk B, tedy tvoje M. A tudiz tvoje L ho nezajima, protoze tu uz zaznamenal coby M.
Ty je beres coby udalosti samotne, tedy bez pozorovatele a zablesku, jenom hole udalosti a jejich casy. Verim, ze to je lepsi zpusob po tom, co se osvoji. Tady zahrnujes udalosti 3, ale nejspis se ten vzorec da rozsirit na nekonecne mnozstvi udalosti, i kdyz nakonec jde snad jenom o odecteni te prvni a posledni.
Offline
#148 26. 06. 2018 18:08 — Editoval MichalAld (26. 06. 2018 18:11)
Re: Relativita Soucasnosti
Zvedavec 4 napsal(a):
Celkem to chapu, ty tady ale rozsirujes ten uz prodlouzeny vzorec na 3 udalosti.
To těžko. To je úplně stejná hloupost, jako bys řekl, že vzorec pro vzdálenosti (mezi dvěma body) rozšiřuji na 3 body. To je přece nesmysl. Maximálně můžu počítat vzdálenost mezi každou dvojcí bodů. Se "vzdáleností v čase" je to úplně stejné.
Zvedavec 4 napsal(a):
Ja to ciste vice mene opakuju po wiki, kde tedy povazujou jen ty dve udalosti, ktere maji vliv na priklad, kterym jenom chteji znazornit princip RS.
Buď to dělají blbě už na té wiki, nebo to děláš blbě ty. Ale pokud jsou v situaci 3 události, tak tam jsou 3 události. Můžeme jednu z nich ignorovat, ale ona kvůli tomu nepřestane existovat.
Zvedavec 4 napsal(a):
Vim, ze to vis, ale bere se to, v mem porozumeni, z hlediska pozorovatele v udalosti/bode A, kdy ho prece nebude zajimat, ze se ten zablesk v B stal ve skutecnosti driv.
"Pozorovatele" to zajímat nemusí, ale vesmír a jeho fyzikální zákony to zajímat bude.
A ta relativita současnosti se týká právě těch událostí, co jsem označil K a L. Nemůžeš prohlásit, že tě "událost L nezajímá, protože...". Vesmír a jeho fyziku zase nezajímá tvůj "pozorovatel" a "to, že tě něco nezajímá".
Zvedavec 4 napsal(a):
Ty je beres coby udalosti samotne, tedy bez pozorovatele a zablesku, jenom hole udalosti a jejich casy. Verim, ze to je lepsi zpusob po tom, co se osvoji.
Né, to není "lepší způsob", to je jediný správný způsob. Je mi líto.
Zvedavec 4 napsal(a):
Tady zahrnujes udalosti 3, ale nejspis se ten vzorec da rozsirit na nekonecne mnozstvi udalosti, i kdyz nakonec jde snad jenom o odecteni te prvni a posledni.
Vzorec se nedá rozšířit, stejně jako se nedá rozšířit vzorec na vzdálenost mezi dvěma body v prostoru. Ale to už jsem psal. Musíš sám vědět, jaká vzdálenost tě zajímá. Dobu (časový interval, "vzdálenost v čase") lze počítat jen mezi dvěma událostmi. A sám si musíš zvolit, které dvě to budou.
Pokud chceš demonstrovat efekt relativity současnosti, musíš si zvolit ty události K, L. Mezi událostmi K a M, ani mezi událostmi L a M žádná relativita současnosti nenastane, jejich pořadí je určeno jednoznačně.
Události K a L nemusí být vůbec žádné záblesky, můžeš klidně uvažovat, že událost K znamená, že se v bodě A narodila malá Anastázie Klímová, v čase t, a událost L znamená, že se v bodě B zrovna narodil malý Bořivoj Liška, v čase t - 1ms. Uznávám, že stanovovat okamžik narození dítěte s přesností na milisekundu je trochu ošemetné, ale astrologové s tím nakonec taky nemají problém...tak co bychom ho měli mít my.
A relativita současnosti znamená, že nelze jednoznačně určit, které z dětí se narodilo první. V jisté souřadné soustavě se mohli narodit i současně.
Posílat si navzájem radiotelegramy obsahující zprávy o narození těch dětí (jako ta událost M) už na relativitu současnosti žádný vliv nemá.
A pokud tvrdíš, že vlastní narození malého Bořivoje pro tebe žádná událost není, že tě to vůbec nezajímá, že ta správná událost je až když ti dorazí "dopis" se zprávou o jeho narození - no, sám přece musíš vidět, že je to uhozené, takto uvažovat. Vesmír to "ví", že se narodil, a že to nezajímá zrovna tebe je mu úplně ukradené.
Celý trik je hlavně v tom, že pro tebe, jako "porodní dulu" u malé Anastázie, existuje krátký časový okamžik, kdy nemůžeš jednoznačně říct, jestli se malý Bořivoj už narodil, nebo ještě né. Ten okamžik netrvá dlouho, shodou okolností trvá přesně těch 600km/c, tedy ty 2ms. 2 milisekundy nejsi schopný říct, jestli už je narozen nebo není - protože i když ve tvé soustavě už narozený je, v jiné ještě není. To je ten hlavní zázrak.
Offline
#149 27. 06. 2018 04:17 — Editoval Zvedavec 4 (27. 06. 2018 05:30)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Relativita Soucasnosti
Me ty dva priklady z wiki objasnily jak RS pracuje a taky potvrdily, ze to nejak tak musi byt. Verim, ze me RS ted rozumim dobre.
Ty tvoje rozsirene rovnice to pro mne ze zacatku trochu zkomplikovaly, ale jsem rad, ze jsi je sem uved, protoze s nima je to kompletni.
Musim to brat tak, ze z vedeckeho hlediska, intuice, ktera se snad vetsinou neda dokazat anebo i presne vysvetlit, protoze to je plne osobni pohled, musi byt podporena matematicky, protoze to je jediny konkretni zpusob, jak to jasne vysvetlit vsem. A asi proto ten pohled bez pozorovatelu a zablesku je lepsi anebo i jediny spravny, jak jsi napsal.
RS je dobry hlavolam a zda se opravdu jako nejakej zazrak, jak pises. A jejim vyvrcholenim pak musi byt ten Paradox Andromedy.
Kdyz a pokud temto ted rozumim, myslim si, ze to tak muze byt, ale nekde jsem se docet, ze ten Paradox pry pracovat nemuze, ale duvody tam nebyly. Je ti znamo proc by mel nebo nemel pracovat?
Offline
#150 27. 06. 2018 15:18
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Relativita Soucasnosti
MichalAld napsal(a):
Zvedavec 4 napsal(a):
Tady zahrnujes udalosti 3, ale nejspis se ten vzorec da rozsirit na nekonecne mnozstvi udalosti, i kdyz nakonec jde snad jenom o odecteni te prvni a posledni.
Vzorec se nedá rozšířit, stejně jako se nedá rozšířit vzorec na vzdálenost mezi dvěma body v prostoru. Ale to už jsem psal. Musíš sám vědět, jaká vzdálenost tě zajímá. Dobu (časový interval, "vzdálenost v čase") lze počítat jen mezi dvěma událostmi. A sám si musíš zvolit, které dvě to budou.
Rozumim tomu. A neni tohle co oni tam na te wiki udelali v tech dvou zadanich? Pouzili jen ty dve udalosti, ktere ukazuji holy princip RS, tedy zaznamenani tech zablesku tim pozorovatelem v A.
MichalAld napsal(a):
Pokud chceš demonstrovat efekt relativity současnosti, musíš si zvolit ty události K, L. Mezi událostmi K a M, ani mezi událostmi L a M žádná relativita současnosti nenastane, jejich pořadí je určeno jednoznačně.
Verim, ze i tohle mi je jasne. Je to detajlnejsi rozbor, ktery ukazuje skutecne, co se tam udalo a tak je jasne presnejsi. Nesnazil jsem se to vyvratit, jenom me to trochu zaskocilo, protoze mne ze zacatku, pod dojmem tech prikladu z wiki, zajimaly jen ty viditelny zablesky.
MichalAld napsal(a):
Události K a L nemusí být vůbec žádné záblesky, můžeš klidně uvažovat, že událost K znamená, že se v bodě A narodila malá Anastázie Klímová, v čase t, a událost L znamená, že se v bodě B zrovna narodil malý Bořivoj Liška, v čase t - 1ms. Uznávám, že stanovovat okamžik narození dítěte s přesností na milisekundu je trochu ošemetné, ale astrologové s tím nakonec taky nemají problém...tak co bychom ho měli mít my.
A tohle definitivne osvetluje, bych si myslel, jak se pohled z matematickeho hlediska lisi od pouheho pohledu intuitivniho, protoze zablesky je celkem jednoduche si predstavit a pouzit tu predstavu k intuitivnimu pochopeni, ale ten druhy pristup se neobejde bez pouziti matematiky, protoze v nem je treba rozumet souradnicim.
Myslim, ze tohle je, co mi tady rikas.
Offline