Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Stejnoměrná konvergence funkční posloupnosti
#1 24. 07. 2018 21:58 — Editoval žabí hněv (24. 07. 2018 22:39)
Stejnoměrná konvergence funkční posloupnosti
Ahoj,
Potřeboval bych prosím radu, jak zjistit zda je daná funkční posloupnost stejnoměrně konvergentní.
f_n(x) = x^n - x^2n .... x leží v uzavřeném intervalu <0,1>
Vypočítal jsem f(x) = 0.
Nevím jak vypočítat supremum(maximum) f_n(x). Rozhodnout o stejnoměrné konvergenci jsem zkoušel přes postačující podmínku integrovatelnosti limitní funkce a to mi jen řeklo, že může nebo nemusí být daná funkční posloupnost stejnoměrně konvergentní.
Offline
#2 24. 07. 2018 23:16 — Editoval vlado_bb (24. 07. 2018 23:17)
Re: Stejnoměrná konvergence funkční posloupnosti
↑ žabí hněv: Takze tvrdis, ze bodova limita je 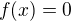 , ano? Aby si zistil, ci ide aj o rovnomernu limitu, odporucam vsimnut si extremy funkcii
, ano? Aby si zistil, ci ide aj o rovnomernu limitu, odporucam vsimnut si extremy funkcii 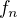 , teda hodnoty v nich. Maxima najdes obvyklym sposobom, pomocou derivacie.
, teda hodnoty v nich. Maxima najdes obvyklym sposobom, pomocou derivacie.
Offline
#4 25. 07. 2018 05:21
Re: Stejnoměrná konvergence funkční posloupnosti
↑ MichalAld:
Ahoj, no rozložil jsem si to takto : f_n(x) = x^n(1-x^n)
Pro x z intervalu [0,1) je f(x) =0
Pro x =1 je f(x) =0
Já mám v poznámkách toto (nerozumím tomu) :
Substituce x^n =T ...rozumím
T(1-T) = T-T^2 = 1/4-(T-1/2)^2 ...rozumím
Ale pak mám napsáno T=1/4 je maximum, tomu nerozumím, ani jsem to nederivoval...
Jinak pokud jsem postupoval dle postupu najdi maximum přes derivace f_n(x) = x^n(1-x^n) , tak jsem ztracen.
Offline
#5 25. 07. 2018 06:28
Re: Stejnoměrná konvergence funkční posloupnosti
↑ žabí hněv: 1. Aky je problem s derivaciou funkcie  ?
?
2. Aky je (pre studenta vysokej skoly) problem s pouzivanim LaTeX-u?
Offline
#6 25. 07. 2018 06:50
Re: Stejnoměrná konvergence funkční posloupnosti
↑ vlado_bb:
Píši na telefonu. Jsem v práci a nemám moc času na hledání symbolů v TeXu. Velice se za to omlouvám. Nicméně jsem student dálkového studia v 1. ročníku a k TeXu jsem se ješte nedostal.
K té derivaci se dostanu odpoledne, napíši svůj postup a řešení v TeXu. Všem děkuji za rady.
Offline
#7 25. 07. 2018 07:01
Re: Stejnoměrná konvergence funkční posloupnosti
Ahoj ↑ žabí hněv:,
Tvoje poznamky su nepresne.
Malo by to byt, napr.
Vieme (zo SS)
To nam okamzite da, ze pre  vyraz
vyraz  je maximum ktore je
je maximum ktore je  .
.
Co ti umoznuje najst aj Max. tvojej funkcie aj bez derivacie....
Inac, mozes aj pouzit, ze sucin dvoch faktorov konstatneho suctu je maximalny ak tie faktory su rovnake.
Co sa tyka tvojho cvicenia ↑ žabí hněv:, mozes si overit tvoje riesenie aj tu https://cs.m.wikipedia.org/wiki/Stejnoměrná_konvergence
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 25. 07. 2018 07:03
Re: Stejnoměrná konvergence funkční posloupnosti
↑ žabí hněv:
Poznamka. Aj ja som pisal z telefonom 👍😁
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 25. 07. 2018 07:20
Re: Stejnoměrná konvergence funkční posloupnosti
žabí hněv napsal(a):
↑ vlado_bb:
K té derivaci se dostanu odpoledne, napíši svůj postup a řešení v TeXu.
Moj postup je takyto:
1. Najst bodovu limitu
2. Najst hodnoty maxim funkcii 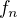 .
.
3. Vyslovit zaver o rovnomernej konvergencii.
Ale pockame si na tvoju derivaciu.
Offline
#10 25. 07. 2018 14:48
Re: Stejnoměrná konvergence funkční posloupnosti
žabí hněv napsal(a):
↑ MichalAld:
Ahoj, no rozložil jsem si to takto : f_n(x) = x^n(1-x^n)
No a může se to takto dělat? U řad které obecně nekonvergují ?
Když vezmu řadu
1 - 1 + 1 - 1 + 1 - 1 ...
(1 - 1) + (1 - 1) + (1 - 1) ...
1 + (-1 + 1) + (-1 + 1) + (-1 + 1) ...
Který z těch dvou součtů je správný ?
Offline
#11 25. 07. 2018 15:42
Re: Stejnoměrná konvergence funkční posloupnosti
↑ MichalAld:
S nekonečnými řadami nelze obvykle zachazet jako s konečnymi řadami. Ne vždy lze užít analogie k asociativnímu zákonu pro sčítání
Offline
#12 25. 07. 2018 15:54
Re: Stejnoměrná konvergence funkční posloupnosti
↑ žabí hněv:
No právě, jenže přesně to zrovna děláš....
Offline
#13 25. 07. 2018 16:21
Re: Stejnoměrná konvergence funkční posloupnosti
↑ vlado_bb:
Takže postupoval jsem stejně.
1. Bodová limita 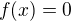
2. Hodnoty maxim :
Po zderivování jsem řešil rovnici :  během úprav neuvažuji
během úprav neuvažuji  , neboť pro
, neboť pro  je
je 
Vyšel mi výsledek : 
Funkční posloupnost nabývá kladných hodnot pro 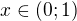 Pro
Pro  a
a  nabývá funkční posloupnost hodnoty nula. Z toho mi plyne závěr, že
nabývá funkční posloupnost hodnoty nula. Z toho mi plyne závěr, že  je lokální maximum.
je lokální maximum.
3.
Po dosazení do  počítám
počítám  , což nesplňuje nutnou podmínku stejnoměrné konvergence, tedy daná funkční posloupnost není stejnoměrně konvergentní na daném intervalu.
, což nesplňuje nutnou podmínku stejnoměrné konvergence, tedy daná funkční posloupnost není stejnoměrně konvergentní na daném intervalu.
Offline
#14 25. 07. 2018 16:22
Re: Stejnoměrná konvergence funkční posloupnosti
↑ MichalAld:
Já se ale nezabývám funkčními řadami,ale posloupnostmi
Offline
#16 25. 07. 2018 16:37 — Editoval žabí hněv (25. 07. 2018 16:38)
Re: Stejnoměrná konvergence funkční posloupnosti
↑ MichalAld:
Ano moje nepřesnost. Omlouvám se. Kdybych to psal v TeXu jak mi bylo výše vytknuto, tak bych Vás nepopletl.
Offline
#17 25. 07. 2018 16:57 — Editoval MichalAld (25. 07. 2018 17:07)
Re: Stejnoměrná konvergence funkční posloupnosti
žabí hněv napsal(a):
Vyšel mi výsledek :
Pak mi to vychází taky tak, i když mi dalo chvíli práce, než jsem pochopil, že tvůj výsledek je stejný jako můj, tedy že:![kopírovat do textarea $x=10^{\frac{-\log_{10}2}{n}} = \sqrt[n]{1 \over 2}$](/mathtex/03/03626b60c0c9aaa07523e5f2e5843459.gif)
Je to hezká funkce, taková jednoduchá...když by si člověk nejdřív nakreslil graf (pro několik n), tak by to viděl hned:
(stejnoměrná konvergence je "shora", nestejnoměrná je "zboku", aspoň v běžných případech to tak je)
(kolečkem na myši lze graf zvětšovat)
Offline
#18 25. 07. 2018 19:05
Re: Stejnoměrná konvergence funkční posloupnosti
↑ MichalAld:
je ale zajimavé, že ač to podle těch grafů nevypadá, tak limitní funkce je rovna nule na daném intervalu, a také je to funkce spojitá na daném intervalu z mého příkladu.
Offline
#19 25. 07. 2018 19:24
Re: Stejnoměrná konvergence funkční posloupnosti
No jo, to je právě ta konvergence co není stejnoměrná. Nekonverguje to tak, že by se ten "hrb" zmenšoval, ale tak, že se zužuje. Až zcela zmizí, v limitě.
A že je ta limitní funkce (na zadaném intervalu) spojitá - já nevím, jestli je to úpnlě přesné. v těch krajních bodech (v tomto případě v bodě 1) je spojitá jen zleva. Zprava už né.
Myslím, že dokonce platí nějaká věta, že když ta limitní funkce je nespojitá (a nemusí být takto, až do nekonečna, stačí kdy má jen "schod"), tak k ní funkční řada nemůže konvergovat stejnoměrně. V blízkosti toho "schodu" to bude vždy konvergovat nějak tak "zboku".
Já nejsem matematik, neznám ty důkazy a teorii kolem toho - ale v teorii signálů se běžně používá tzv. Fourierova řada - že se nějaká funkce rozkládá na součet sinusovek s frekvencemi  . A když má ta limitní funkce nespojitost (u signálů se tomu říká skok), tak to k ní vždy konverguje taky takto zboku. Kolem toho zkoku se objeví takové "zákmity" a jejich velikost už s přidáváním dalších frekvencí neklesá, jen se zkracuje doba, kterou trvají.
. A když má ta limitní funkce nespojitost (u signálů se tomu říká skok), tak to k ní vždy konverguje taky takto zboku. Kolem toho zkoku se objeví takové "zákmity" a jejich velikost už s přidáváním dalších frekvencí neklesá, jen se zkracuje doba, kterou trvají.
Můžeš si to sám zkusit, třeba http://www.falstad.com/fourier/Fourier.html
Offline
#20 27. 07. 2018 17:52
Re: Stejnoměrná konvergence funkční posloupnosti
Ahoj ↑ žabí hněv:,
Tu mas uzitocne citanie https://notendur.hi.is/vae11/Þekki … _rudin.pdf
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#21 31. 07. 2018 11:25 — Editoval Brano (31. 07. 2018 11:29)
Re: Stejnoměrná konvergence funkční posloupnosti
↑ MichalAld:
limitna funkcia je spojita na uvazovanom intervale.
plati veta: 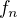 su spojite a konverguju rovnomerne (na [0,1]) k
su spojite a konverguju rovnomerne (na [0,1]) k  , potom
, potom  musi byt spojita
musi byt spojita
naopak to platit nemusi, teda spojite funkcie mozu konvergovat bodovo k spojitej funkcii a ta konvergencia nemusi byt rovnomerna; prikladom je tento priklad
aj ked da sa ta veta otocit ciastocne, napr. Diniho Veta
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Stejnoměrná konvergence funkční posloupnosti
