Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 07. 2018 14:15
Soustava kvadratických rovnic
Prosím vás, mohl by mi někdo poradit jaký je poslední krok v řešení této soustavy:
x^2+xy+y^2=19
x^2+2xy-y^2 =7
Školním postupem jsem zatím došla k tomu že jsem to sečetla, tím se eliminovalo y^2. Výsledek se dá vytknout na x(2x+3y)=26. A pak už jsem v koncích. Ve škole jsme to řešili rozložením 26 na všechny kombinace 2 činitelů (přirozených), a potom každý dosadit jako x a dopočítat y. To jsem udělala... Mělo mi vyjít [1;8] a [26;-26/3] (pokud jsem si to tedy před víc než rokem dobře zapsala). Vyšlo mi to první, pak 2) [26;53/3],3) [2;3], 4)[13;-8].
Zkouška mi vychází jen u 3). (takže to, co mám zapsané že měl být výsledek, je asi blbě). Nejsem si jistá, jestli jsem tem poslední krok udělala správně. Navíc x by mohl být stejně tak dobře nějaký zlomek, což to komplikuje ještě víc...
Prosím vás, jakým způsobem to tedy dořešit? (grafem nemůžu, kuželosečky jsme ještě nebrali a pochybuju, že bych je sama pochopila tak abych to mohla použít...)
"Když ji miluješ, je pořád co řešit..."
Offline
- (téma jako vyřešené označil(a) Kate X)
#2 27. 07. 2018 20:57
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Soustava kvadratických rovnic
Zdravím,
Navíc x by mohl být stejně tak dobře nějaký zlomek, což to komplikuje ještě víc...
to máš pravdu, pokud nevíme, z jakého číselného oboru jsou x, y, pouhým rozkladem na činitele výrazu x(2x+3y)=26 nemůžeme prokázat, že máme podchycené všechny kořeny. Zkusila bych metodu dosazovací.
Z 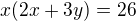 je
je 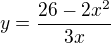 , dosazení do 1. rovnice vede na rovnici 4. stupně, která ale půjde řešit substituci (pokud jsem neudělala nějakou chybu při pokusu úprav).
, dosazení do 1. rovnice vede na rovnici 4. stupně, která ale půjde řešit substituci (pokud jsem neudělala nějakou chybu při pokusu úprav).
Zatím nevidím nějakou jinou "hezkou metodu" úprav původní soustavy, ale ještě se podívám. Mohli jste používat dosazovací metodu? Děkuji za upřesnění.
Offline
#3 27. 07. 2018 22:27
Re: Soustava kvadratických rovnic
Nejspíš mohli, taky jsme se ji učili, i když zrovna tohle mám pocit byl vzorový příklad (i když v tom případě nevím, proč jsme to řešili tak divně)
Díky za radu, zkouším tvůj postup, i když zatím někde asi pořád dělám chybu, protože se nemůžu zbavit třetí a první mocniny, takže k substituci jsem ještě nedošla...
"Když ji miluješ, je pořád co řešit..."
Offline
#4 27. 07. 2018 23:18
Re: Soustava kvadratických rovnic
Zdravím, měla by ti vyjít rovnice: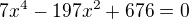
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#5 29. 07. 2018 17:29
#6 30. 07. 2018 10:46 — Editoval Rumburak (31. 07. 2018 12:53)
Re: Soustava kvadratických rovnic
↑ Kate X:
Ahoj. Zkusil bych následující způsob.
Máme tedy soustavu
x^2+xy+y^2=19
x^2+2xy-y^2 =7.
Když do ní dosadíme y = 0, dostaneme soustavu x^2=19, x^2 =7, což je spor, takže případ y = 0
nastat nemůže. Odtud plyne, že se nedopustíme chyby, když každou rovnici zadané soustavy vydělíme
výrazem y^2, který je nutně také nenulový.
Obdržíme tak soustavu
 ,
,
v níž provedeme substituci  . Dojdeme tak k soustavě
. Dojdeme tak k soustavě
 .
.
Odečtením druhé rovnice od první obdržíme lineární vztah mezi neznámými  .
.
EDIT. Nebo můžene ihned vyloučit ze soustavy proměnnou  (která je v obou rovnicích jen v první mocnině)
(která je v obou rovnicích jen v první mocnině)
a tím obdržet kvadratickou rovnici o neznámé  . Dále snad jasné.
. Dále snad jasné.
Offline

![kopírovat do textarea $\[-\frac{13\sqrt 7}{7}; \frac{4\sqrt 7}{7}\]$](/mathtex/28/280a435e3cdf91b9238da454dee3be04.gif)
![kopírovat do textarea $\[\frac{13\sqrt 7}{7}; -\frac{4\sqrt 7}{7}\]$](/mathtex/97/9788c089a8f17e09de9ebf103965d643.gif)
![kopírovat do textarea $\[2; 3\]$](/mathtex/51/5171f96aca3d2346e33dae0e72fbe450.gif)
![kopírovat do textarea $\[-2; -3\]$](/mathtex/91/9166786846aa6966a7918a6dc8f26f57.gif)

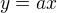
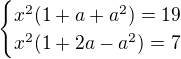
 pak obyčejnou kvadratickou rovnici
pak obyčejnou kvadratickou rovnici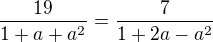
 ,
, 