Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 08. 2018 18:19 — Editoval laszky (04. 08. 2018 19:46)
Poreznost
Behem cteni jedne knihy me napadla jedna zajimava "letni" uloha
Pri modelovani proudeni v poreznim prostredi je poreznost tohoto prostredi definovana jako podil prazdneho mista ku celkovemu objemu. Tuhe, neprostupne materialy maji tedy poreznost 0, zatimco prazdny prostor ma poreznost 1.
1) Uvazujme 2D model porezniho prostredi, ve kterem jsou castice reprezentovany stejne velikymi kruhy. Predpokladejme, ze kruhy jsou rozmisteny pravidelne tak, ze kazdy kruh se dotyka sesti jinych kruhu. Urcete poreznost tohoto prostredi. Dale uvazujme libovolny rez (primku) timto prostredim a poreznost tohoto rezu definujme jako podil prazdneho mista, ktere rez protina, ku celkove delce rezu. Urcete, jakych hodnot muze poreznost rezu nabyvat.
2) Analogicky postupujte i ve 3D v pripade kouli. Urcete rozlozeni kouli s minimalni poreznosti a tuto poreznost spoctete. Dale uvazujte libovolny 2D rez (rovinu) timto prostredim a urcete, jakych hodnot muze poreznost tohoto rezu nabyvat.
Pozn.I.: Jelikoz nejsou v pripade 1) prazdne prostory mezi kruhy spojeny, je takovy prostor neprostupny a poreznost v tomto pripade nedava prilis smysl. Presto ji lze spocitat.
Pozn.II.: V pripade cele roviny (celeho prostoru) lze jen velmi tezko hovorit o "celkovem objemu". Proto vzdy uvazujte dostatecne velkou oblast, napr. rovnostranny trojuhelnik (resp. ctyrsten) o delce strany  ,
, 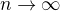 .
.
Online