Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 26. 12. 2015 02:41 — Editoval liamlim (26. 12. 2015 02:45)
Re: Něco jako kombinační čísla



To jsou všechno moc nepěkné vstupní podmínky. Po chvilce přemýšlení jsem došel k lepšímu zápisu. Napíši ho zde jen pro úplnost, kdyby toto někdo někdy četl. pro
pro 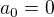
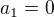


Vidíte tedy, že posloupnost je definována úplně stejně. Jediný rozdíl je ve vstupních podmínkách. Ono tato posloupnost se snad bude i trochu lépe zkoumat.
Pozn.:
Všimněte si, že  ,
,  ,
,  řeší rovnici
řeší rovnici  ... Což trochu připomíná definici naší posloupnosti. To zkusím nějak využít. Až budu mít trochu času. Teď bohužel ukrajuji čas z učení se na zkoušky. Ale ono se těžko brání, když jsou to tak zajímavé věci.
... Což trochu připomíná definici naší posloupnosti. To zkusím nějak využít. Až budu mít trochu času. Teď bohužel ukrajuji čas z učení se na zkoušky. Ale ono se těžko brání, když jsou to tak zajímavé věci.
Edit: ve skutečnosti jsem odvodil trochu obecnější vztah. Platí:
Pro posloupnosti  definované stejně až na vstupní podmínky.
definované stejně až na vstupní podmínky.  a
a 
 a
a 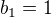
 a
a 
Offline
#27 28. 12. 2015 14:17 — Editoval liamlim (28. 12. 2015 14:34)
Re: Něco jako kombinační čísla
 Ahoj, teď jsem zkusil trochu jiný přístup na VFV, tentokrát je ten postup snad přehlednější, proto bych byl moc rád, kdyby mi někdo naznačil, jestli je můj postup správný.
Ahoj, teď jsem zkusil trochu jiný přístup na VFV, tentokrát je ten postup snad přehlednější, proto bych byl moc rád, kdyby mi někdo naznačil, jestli je můj postup správný.
Pokud  pak
pak 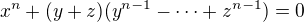
Pozn.: Teď bude trochu víc dočasných proměnných - pro přehlednost je budu číslovat a nikoliv používat abecedu.
Označme si 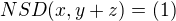 . Pak pro nějaká nesoudělná (2),(3) platí
. Pak pro nějaká nesoudělná (2),(3) platí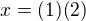

Dále označme  . Pak máme pro nějaká nesoudělná (5), (6):
. Pak máme pro nějaká nesoudělná (5), (6):
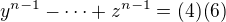
Pozn.: Vše s NSD dokonale funguje, i pokud by náhodou čísla byla nesoudělná. Pak by prostě např (4) bylo (1) a jediné, co bychom zavedením získali, by bylo konstatování nesoudělnosti  a
a 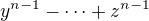 . Stejně tak ale můžeme mnohem obecněji pracovat s nesoudělností (5), (6). Protože předešlý případ je pouze speciálním toho.
. Stejně tak ale můžeme mnohem obecněji pracovat s nesoudělností (5), (6). Protože předešlý případ je pouze speciálním toho.
Už jsme skoro s NSD hotovi. Teď už jen označme 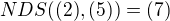 . Pak pro nějaká nesoudělná (8), (9) platí:
. Pak pro nějaká nesoudělná (8), (9) platí:
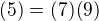
Nyní pozorujme rovnost  a dosaďme.
a dosaďme. 
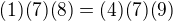

Odkud z nesoudělnosti (8) a (9) okamžitě vidíme, že (8) dělí (4) a (9) dělí (1). Proto existují (10), (11) takové, že:

Po dosazení máme  neboli
neboli  . Zpětně dosadíme do
. Zpětně dosadíme do  . Nyní již máme jen jedno vyjádření pro
. Nyní již máme jen jedno vyjádření pro  namísto dvou (obě vyjdou stejná). A to:
namísto dvou (obě vyjdou stejná). A to:
dále:

Toto dosaďme do 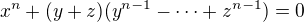
 Pro
Pro 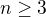 můžeme vydělit:
můžeme vydělit:
Odsud vidíme několik zajímavých faktů. Nejprve  . Což plyne z toho, že (7)^n podle poslední rovnosti dělí (3)(6). Jenže (7) zároveň dělí (2), které je nesoudělné s (3) a zároveň (5), které je nesoudělné s (6). Což stačí pro to, aby (7) bylo rovno 1.
. Což plyne z toho, že (7)^n podle poslední rovnosti dělí (3)(6). Jenže (7) zároveň dělí (2), které je nesoudělné s (3) a zároveň (5), které je nesoudělné s (6). Což stačí pro to, aby (7) bylo rovno 1.
Dále  dělí (6), protože je nesoudělné s (3). Což plyne z faktu, že (8) dělí (2).
dělí (6), protože je nesoudělné s (3). Což plyne z faktu, že (8) dělí (2).
Dále  dělí (3), protože je nesoudělné s (6). Což plyne z faktu, že (9) dělí (5).
dělí (3), protože je nesoudělné s (6). Což plyne z faktu, že (9) dělí (5).
Proto existují (12),(13) takové, že  a
a  . Po dosazení všude kam můžeme dostaneme:
. Po dosazení všude kam můžeme dostaneme:

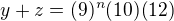

Pozn2: Asi jste si všimli, že vůbec neřeším znaménka. Ale pouze dělitelnosti. U všeho, co jsem dosud zmínil a zmíním znaménka vůbec nejsou důležitá. Chci vyvozovat obecná fakta.
Tak.. Upravme nyní  Trochu jiným způsobem:
Trochu jiným způsobem: .
.
Využiji toho, že jsme s v tomto tématu o číslech  dozvěděli několik věcí. Tak za prvé. Pokud budeme brát
dozvěděli několik věcí. Tak za prvé. Pokud budeme brát  liché, pak
liché, pak  . Taky
. Taky  , což ale využiji až za chvilku. To znamená, že můžeme vytknout
, což ale využiji až za chvilku. To znamená, že můžeme vytknout 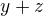 . Dostaneme:
. Dostaneme: .
.
Odsud snadno vidíme, že 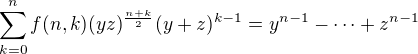 . Odsud snadno vidíme, že jakýkoliv společný dělitel čísel
. Odsud snadno vidíme, že jakýkoliv společný dělitel čísel 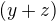 a
a  dělí
dělí  . Odkud snadno, pokud BÚNO připustíme, že
. Odkud snadno, pokud BÚNO připustíme, že  a
a  jsou nesoudělná, vidíme, že jakýkoliv společný dělitel těch čísel dělí
jsou nesoudělná, vidíme, že jakýkoliv společný dělitel těch čísel dělí  . Tedy i
. Tedy i  dělí
dělí  . Podívejme se na vztahy
. Podívejme se na vztahy 
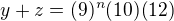

Z toho, že jakýkoliv společný dělitel čísel 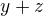 a
a  dělí
dělí  vidíme, že nutně jedno z čísel
vidíme, že nutně jedno z čísel  nebo
nebo  je rovno (v absolutní hodnotě) číslu
je rovno (v absolutní hodnotě) číslu  a druhé je rovno 1. Taky vidíme, že (10) je nutně 1 nebo
a druhé je rovno 1. Taky vidíme, že (10) je nutně 1 nebo  (Zde přidávám BÚNO požadavek na
(Zde přidávám BÚNO požadavek na  je prvočíslo). Přitom pokud je rovno
je prvočíslo). Přitom pokud je rovno  pak odsud
pak odsud  dělí
dělí  .
.
Stejný postup bychom mohli aplikovat na  a
a  . Z předpokladu nesoudělnosti
. Z předpokladu nesoudělnosti  a
a  pak okamžitě dostáváme, že číslo odpovídající (10) bude pro alespoň dvě z čísel
pak okamžitě dostáváme, že číslo odpovídající (10) bude pro alespoň dvě z čísel  ,
, 
 rovno 1. BÚNO nechť tato jistá dvojice je
rovno 1. BÚNO nechť tato jistá dvojice je  a
a  . Pak již odsud vidíme, že nutně pro nějaká nesoudělná
. Pak již odsud vidíme, že nutně pro nějaká nesoudělná 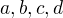 platí:
platí:
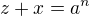

 .
.
Pokud (10) = 1 i v našem případě (u x) pak bude platit analogická rovnost. Já chci ukázat, že to tak musí nutně být. Takže.. Sporem. Pro spor nechť  . Pak je
. Pak je  dělitelné
dělitelné  ale taky
ale taky  je dělitelné
je dělitelné  . Na chvíli zkusme, aby
. Na chvíli zkusme, aby  dělilo
dělilo  . Ze vztahu
. Ze vztahu 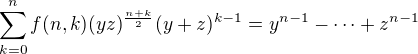 pak snadno dostáváme, že
pak snadno dostáváme, že  dělí
dělí  , což není možné. Proto nutně
, což není možné. Proto nutně  a
a  . Tedy
. Tedy


(tak, tady s přepisováním prozatím končím). Dosud jsou mé myšlenky docela jasné (i když možné chybné). Ale odteď si to potřebuji trochu ujasnit. BTW asi to jde vše odvodit mnohem jednodušeji. Ono by bohatě stačilo ukázat, že 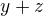 je skoro vždy nesoudělné s
je skoro vždy nesoudělné s  . Teď mě napadá, že možná by se tomu všemu s NSD dalo úplně vyhnout. No ale mazat to nebudu když už jsem to napsal.
. Teď mě napadá, že možná by se tomu všemu s NSD dalo úplně vyhnout. No ale mazat to nebudu když už jsem to napsal.
Offline
#28 11. 02. 2017 18:27
Re: Něco jako kombinační čísla
Tak mám po delší době jiná čísla, která vykazují jistou podobnost s kombinačními. Uvedu to sem pro zajímavost:
Uvažme čísla definovaná jako ![kopírovat do textarea $[n,k] = 0$](/mathtex/00/00107c8af6d8decd32eb6096e7a33ad2.gif) pro
pro  a
a  a
a  . Dále
. Dále ![kopírovat do textarea $[1,1] = 1$](/mathtex/0a/0a8714cb466da072dd5cc7945fde4b41.gif) . Dále tato čísla splňují:
. Dále tato čísla splňují:![kopírovat do textarea $[n + 2, k + 2] = 2[n + 1, k + 2] - [n,k]$](/mathtex/d8/d868ed3c36e6a1fa7d9bccbfee1e4a57.gif)
(doporučuji nakreslit si čísla do trojúhelníku podobného Pascalovu, pak se trojúhelník vyplňuje celkem rychle).
Pak platí ![kopírovat do textarea $\sum_{k=1}^n[n,k] = 1$](/mathtex/86/8666243103dcc08de38a440b44346934.gif) . Umíte to dokázat? Já mám docela trikový důkaz, který se mi tak úplně nechce sem psát. Využívá toho, že
. Umíte to dokázat? Já mám docela trikový důkaz, který se mi tak úplně nechce sem psát. Využívá toho, že 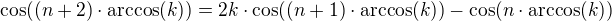 ... To se mi nelíbí. Tento důkaz bych rozhodně nebyl schopen vymyslet - samotné tvrzení o součtu, který je roven 1 jsem totiž odvodil přímo z uvedené identity. Kdybych nevěděl, že je třeba ji použít, pak bych byl naprosto ztracen.
... To se mi nelíbí. Tento důkaz bych rozhodně nebyl schopen vymyslet - samotné tvrzení o součtu, který je roven 1 jsem totiž odvodil přímo z uvedené identity. Kdybych nevěděl, že je třeba ji použít, pak bych byl naprosto ztracen.
Offline
#29 13. 02. 2017 19:29
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Něco jako kombinační čísla
↑ liamlim:
Ahoj, nestačila by indukce podle n? Pak z toho rekurentního vztahu sumací přes k získám na pravé straně 2.1-1, což je 1...
"Máte úhel beta." "No to nemám."
Offline
#30 14. 02. 2017 00:11
Re: Něco jako kombinační čísla
Poznamka.
Rekurentnu relaciu, 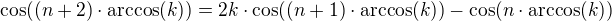 pozname ako relaciu pre Tchebysevove polynomy ptrveho druhu....
pozname ako relaciu pre Tchebysevove polynomy ptrveho druhu....
Nahoda??
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#31 14. 02. 2017 00:12 — Editoval liamlim (14. 02. 2017 00:27)
Re: Něco jako kombinační čísla
↑ vanok:
Uff o něčem takovém jsem v životě neslyšel :D
edit: platí to i pro siny, neboli:
Tomu se říká druhého druhu? Já jsem si tyto vzorečky odvodil a připadaly mi zajímavé. Vůbec jsem netušil, že už mají nějaký zavedený název. Zkusím o nich něco najít. Děkuji.
edit: odvození těch vztahů není těžké. stačí využít  a potom dosadit
a potom dosadit  a
a 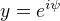 a podívat se na reálné a imaginární části... Pak už je jednoduché vymyslet dosazení, ze kterého ty vztahy pěkně plynou.
a podívat se na reálné a imaginární části... Pak už je jednoduché vymyslet dosazení, ze kterého ty vztahy pěkně plynou.
Offline
#32 14. 02. 2017 08:38
Re: Něco jako kombinační čísla
Ano. Presne tak.
Pozri tu https://en.m.wikipedia.org/wiki/Chebyshev_polynomials a aj tu https://fr.m.wikipedia.org/wiki/Polynôme_de_Tchebychev.
Teoria numerickej matematiky je velmi pekna.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#33 04. 08. 2018 22:52 — Editoval liamlim (04. 08. 2018 23:01)
Re: Něco jako kombinační čísla
Trochu jsem si dnes upravoval a došel jsem k následujícímu (píši pro úplnost a jen pro liché  , pro sudé je to snadné a nechávám na čtenáři):
, pro sudé je to snadné a nechávám na čtenáři):
Nechť  je liché. Pak:
je liché. Pak:
Připadá mi to celkem zajímavé! Vždyť jsme před více než rokem k podobně hezkému vzorečku nedošli.
Edit:
Obecně platí následující:
Offline
