Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 08. 2018 10:58 — Editoval žabí hněv (14. 08. 2018 10:59)
Definiční obor funkce
Ahoj, mám určit definiční obor funkce 
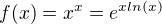
tento výraz má smysl pro 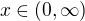
tedy interval 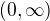 bude podmnožinou definičního oboru funkce
bude podmnožinou definičního oboru funkce
Pokud uvažuji  , tak
, tak  je neurčitý výraz, tedy v
je neurčitý výraz, tedy v  není funkce definovaná?
není funkce definovaná?
A jak je to s  ? Mohu
? Mohu 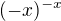 přepsat na
přepsat na  Tedy tento výraz má smysl i pro všechna
Tedy tento výraz má smysl i pro všechna 
Takže výsledný definiční obor této funkce bude  ?
?
Děkuji za rady
Offline
#2 14. 08. 2018 11:17 — Editoval Rumburak (14. 08. 2018 11:20)
Re: Definiční obor funkce
↑ žabí hněv:
Ahoj.
Případ  je složitější, např.
je složitější, např.  .
.
Obecně ovšem záleží na zvoleném "základním" číselném oboru (reálná čísla vs. komplexní čísla).
Probírali jste teorii funkcí komplexní proměnné, speciálně teorii analytických funkcí?
Offline
#3 14. 08. 2018 11:27 — Editoval žabí hněv (14. 08. 2018 13:40)
Re: Definiční obor funkce
↑ Rumburak:
Myslím, že jde o reálná čísla. Předmět je M1.
Je tedy ten definiční obor spravně? A ta úvaha ohledně bodu x=0 je také spravná ? Někde jsem četl, že  jak to tedy je?
jak to tedy je?
Offline
#4 14. 08. 2018 14:44 — Editoval Rumburak (14. 08. 2018 15:07)
Re: Definiční obor funkce
↑ žabí hněv:
Za těchto okolností můžeme vzorec  využit pouze pro
využit pouze pro  , kdy všechny výrazy
, kdy všechny výrazy
v něm obsažené nabývají pouze reálných hodnot. Takže částí definičního oboru zkoumané funkce je tedy
určitě interval  , avšak není to definiční obor celý, jak ukazuje příklad
, avšak není to definiční obor celý, jak ukazuje příklad
 .
.
Zkus obdobně vyšetřit případ, kdy je  záporné CELÉ.
záporné CELÉ.
Poznámka.
Symbol  sice standardně definován není, pokud vím, ale kdo chce, může si ho dodefinovat.
sice standardně definován není, pokud vím, ale kdo chce, může si ho dodefinovat.
V tom případě bývá "rozumné" dodefinovat ho hodnotou 1 (napříklsd v teorii mocninných řad - funkce
daná mocninnou řadou a mající kladný poloměr konvergence je pak spojitá ve svém středu, což je
vlastnost zásadního významu). Záleží tedy na tom, jak to zavedl či nezavedl váš učitel daného
předmětu.
Offline
#5 14. 08. 2018 16:31 — Editoval žabí hněv (14. 08. 2018 16:37)
Re: Definiční obor funkce
[re]p570686|Rumburak[/re
Nechal jsem si část průběhu funkce vykreslit v Matlabu :
Co se týká chování funkce pro  , tedy záporné hodnoty
, tedy záporné hodnoty  je funkce ve tvaru
je funkce ve tvaru  a řeším pro která
a řeším pro která  nemá daný výraz(restrikce funkce
nemá daný výraz(restrikce funkce 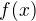 na interval
na interval 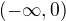 ?) smysl.
?) smysl.
Jmenovatel roven nule, což se pro žádné  nestane, tedy i celý interval
nestane, tedy i celý interval 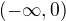 je podmnožinou definičního oboru původní funkce.
je podmnožinou definičního oboru původní funkce.
Dodefinováním  patří i
patří i  do definičního oboru a získávám
do definičního oboru a získávám 
Lze to takto prezentovat?
Děkuji
Offline
#6 14. 08. 2018 16:53 — Editoval jarrro (14. 08. 2018 17:10)
Re: Definiční obor funkce
↑ žabí hněv:↑ žabí hněv: a
a 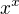 sú iné funkcie.
sú iné funkcie.
V reálnej analýze má 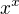 zmysel iba keď
zmysel iba keď![kopírovat do textarea $x>0 \vee x\in\{-\frac{p}{q};\[p,q\]\in\mathbb{N}^2 \& D{\(p,q\)}=1\& \(\(\exists k\in\mathbb{N}_0\)\(q=2k+1\)\)\}$](/mathtex/57/576b7f11a524d02d75bf97ce32f60dcf.gif)
teda napríklad  má zmysel iba v komplexnej analýze
má zmysel iba v komplexnej analýze
Teda pre reálnu fciu f reálnej premennej x definovanú predpisom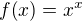 je prirodzený (vyplývajúci zo zmysluplnosti predpisu) definičný obor
je prirodzený (vyplývajúci zo zmysluplnosti predpisu) definičný obor ![kopírovat do textarea $D_f=\(0,\infty\)\cup \{-\frac{p}{q};\[p,q\]\in\mathbb{N}^2 \& D{\(p,q\)}=1\& \(\(\exists k\in\mathbb{N}_0\)\(q=2k+1\)\)\}$](/mathtex/b9/b99385046705cd4f78013274e66e1229.gif)
MATH IS THE BEST!!!
Offline
#8 14. 08. 2018 17:49
Re: Definiční obor funkce
↑ žabí hněv:D(p,q)=1 je že p,q sú nesúdeliteľné (ich najväčší spoločný deliteľ je 1)
MATH IS THE BEST!!!
Offline
#10 14. 08. 2018 18:21
Offline
#13 14. 08. 2018 19:34
#14 14. 08. 2018 21:42
Offline
#16 14. 08. 2018 22:47
Re: Definiční obor funkce
Pozdravujem ↑ jarrro:,
Pozri aj tu
http://www.peda.com/grafeq/gallery/rogu … ntial.html
Kde je tvoj vysledok a aj graf funkcie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

 , kde
, kde  i
i  jsou přirozená čísla,
jsou přirozená čísla,  nerozumím a ta poslední podmínka, že q je liché číslo?
nerozumím a ta poslední podmínka, že q je liché číslo? a
a 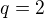 tato dvě čísla nevyhovují tvému tvrzení, a přesto podle mě číslo - 2 patří do definičního oboru.
tato dvě čísla nevyhovují tvému tvrzení, a přesto podle mě číslo - 2 patří do definičního oboru. to vyhovuje podmínce tvojí množiny ne? Přitom třetí odmocnina ze zaporneho cisla take nejde...
to vyhovuje podmínce tvojí množiny ne? Přitom třetí odmocnina ze zaporneho cisla take nejde...![kopírovat do textarea $\(-\frac{1}{3}\)^{-\frac{1}{3}}=\frac{1}{\sqrt[3]{-\frac{1}{3}}}=-\sqrt[3]{3}$](/mathtex/60/60cb5fc475f965bd3758cc329ecdfb40.gif)