Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Derivace s odmocninou - předpoklady (TOTO TÉMA JE VYŘEŠENÉ)
#1 19. 08. 2018 12:13 — Editoval slender (19. 08. 2018 12:14)
Derivace s odmocninou - předpoklady
Zdravím,
řeším následující příklad, ve kterém mám zjednodušit derivaci. 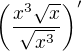
Postupoval jsem následovně (úmyslně to velmi rozepisuji):
Je mi jasné, že v rovnostech předpokládám, že 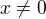 (abych nedělil nulou). Wolfram Alpha však tvrdí, že tam ještě navíc předpokládám, že
(abych nedělil nulou). Wolfram Alpha však tvrdí, že tam ještě navíc předpokládám, že 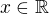 .
.
Poradil by mi někdo, prosím, ve kterém kroce mých úprav nevědomky aplikuji tento předpoklad? (Předem moc díky.)
Offline
- (téma jako vyřešené označil(a) slender)
#2 19. 08. 2018 12:58 — Editoval vanok (19. 08. 2018 13:03)
Re: Derivace s odmocninou - předpoklady
Ahoj ↑ slender:,
Akoze mas, v menovateli 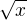 tak musis predpkkadat, ze
tak musis predpkkadat, ze  .( Ty pracujes z realnou funkciou)
.( Ty pracujes z realnou funkciou)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 19. 08. 2018 16:53
Re: Derivace s odmocninou - předpoklady
↑ vanok: Díky za odpověď.
Chápu správně, že ta podmínka  (pro reálné funkce) vznikla z podmínky
(pro reálné funkce) vznikla z podmínky 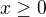 (kvůli
(kvůli 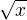 )
)
a podmínky 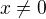 (kvůli
(kvůli  , potažmo
, potažmo 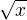 ve jmenovateli)?.
ve jmenovateli)?.
Pokud bych ale pracoval oboru komplexních čísel, odmocniny záporných čísel jsou definované, takže by se podmínka omezila pouze na 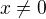 ?
?
↑ MichalAld: Pravda, díky
Offline
#5 19. 08. 2018 17:59
Re: Derivace s odmocninou - předpoklady
slender napsal(a):
Pokud bych ale pracoval oboru komplexních čísel, odmocniny záporných čísel jsou definované, takže by se podmínka omezila pouze na
?
Já jednoduchou odpověď na tvou otázku neznám, nicméně pokud uvažujeme obor komplexních čísel, musíme si uvědomit, že n-tá odmocnina má vždy n možných hodnot.
V oboru reálných čísel jsou maximálně dvě možnosti, kladná a záporná. Takže můžeme snadno definovat, že výsledkem je to kladné číslo.
V komplexním oboru ovšem není tak jednoduché vybrat to jedno z N možných čísel (N-té odmocniny).
Offline
#6 19. 08. 2018 20:20
Re: Derivace s odmocninou - předpoklady
Pozdravujem ↑ MichalAld:,
Mas pravdu vysetrenie komlexnych analytickych funkcii mozes to urobit vdaka Riemannovym plocham.
Tu najdes uvodne citanie https://en.m.wikipedia.org/wiki/Riemann_surface
Osobne som sa take ucil v Master .... je to pekna teoria. ( neviem ci sa take uci aj na technickych smeroch).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 19. 08. 2018 20:44
Re: Derivace s odmocninou - předpoklady
↑ vanok:↑ MichalAld: Díky moc vám oběma za odpovědi, myslím, že jsem se v tom trochu rozkoukal. Nechal jsem se na začátku zmást Wolframem a tím, že v zadání nebylo explicitně určeno, že mám uvažovat reálná čísla.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Derivace s odmocninou - předpoklady (TOTO TÉMA JE VYŘEŠENÉ)