Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Fyzika
- » Piezokryštalický oscilátor budený napäťovým pulzom (TOTO TÉMA JE VYŘEŠENÉ)
#1 13. 08. 2015 20:01
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Piezokryštalický oscilátor budený napäťovým pulzom
Po dlhej dobe opäť zdravím.
Mám malý problém, s ktorým neviem pohnúť. Mám piezokryštalický oscilátor, ktorý je z rovnováhy vybudený napäťovým pulzom a následne nechaný vykonávať volné kmity až do utlmenia.
Pulz je zložený z  harmonických cyklov (sínusovky), amplitúda jedného cyklu je
harmonických cyklov (sínusovky), amplitúda jedného cyklu je  , a uhlová frekvencia cyklu
, a uhlová frekvencia cyklu  . Medzi cyklami v rámci pulzu nie je žiadna pauza, naväzujú jeden na druhý.
. Medzi cyklami v rámci pulzu nie je žiadna pauza, naväzujú jeden na druhý.
Mojim problémom je, že netuším ako vypočítať celkovú amplitúdu pulzu. Rozmýšľal som, že by som na to mohol ísť cestou stredného výkonu, ale neviem, či sa uberám správnym smerom. Časový priebeh voľných kmitov oscilátora je mi známy z homogénnej pohybovej rovnice, dokonca aj výraz pre piezoprúd, ktorý oscilátor pri svojich kmitoch generuje, ale bez amplitúdy napätia prúd nevypočítam.
Viem, že to nepatrí do "elementárnej" vysokoškolskej fyziky, ale potrebujem nástin, aby som sa mohol odpichnúť.
Offline
- (téma jako vyřešené označil(a) Ferdish)
#2 27. 08. 2018 21:37 — Editoval miso16211 (27. 08. 2018 21:45)
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Piezokryštalický oscilátor budený napäťovým pulzom
síce sa veľmi nerozumiem do toho, ale celková amplitúda = súčtu všetkých aplitúd. Problém je, ze kazdý cyklus ma roznu frekvenciu. Neviem č ito nie je blbosť, ale jedine čo ma napadá.
výsledná "vlna"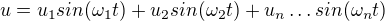 ak u1 je uhlova frekvenica 1. cykla
ak u1 je uhlova frekvenica 1. cykla
najdem maximum - zderivujem a polozim nule a najdem riesenia. Potom len nájdem hodnotu funkcie v daných rieseniach.
Offline
#3 27. 08. 2018 22:09 — Editoval Ferdish (27. 08. 2018 22:14)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Piezokryštalický oscilátor budený napäťovým pulzom
Odpoveď bola medzičasom nájdená. Len som zabudol označiť tému ako vyriešenú, lebo medzitým zapadla do zabudnutia.
Napriek tomu ma udivuje, že si mal odvahu napísať odpoveď na 3 roky starý dotaz...ale neber to v zlom.
Offline
#4 27. 08. 2018 23:56
Re: Piezokryštalický oscilátor budený napäťovým pulzom
Ferdish napsal(a):
Pulz je zložený z
harmonických cyklov (sínusovky), amplitúda jedného cyklu je
, a uhlová frekvencia cyklu
. Medzi cyklami v rámci pulzu nie je žiadna pauza, naväzujú jeden na druhý.
Když už je vlákno znovu otevřené - jak jsi vlastně přesně myslel, že bude ten pulz vypadat ? Já tomu moc nerozumím...
Offline
#5 28. 08. 2018 00:06 — Editoval miso16211 (28. 08. 2018 00:08)
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Piezokryštalický oscilátor budený napäťovým pulzom
↑ MichalAld: podľa mna je problem aj v značení, nerozumiem či pre každý cyklus je amplitúda rovnaká, alebo iná. Zrejme iná, a malo by byť značenie takéto:
amplitúda i - teho cyklu je  a frekvencia
a frekvencia 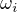
Offline
#6 28. 08. 2018 00:34 — Editoval Ferdish (28. 08. 2018 00:46)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Piezokryštalický oscilátor budený napäťovým pulzom
↑ miso16211:
Už vidím, kde je problém.
Jeden cyklus=jeden harmonický (sínusový) kmit. Cykly naväzujú bezprostredne jeden za druhým, takže 3 cykly=3 kmity, 5 cyklov = 5 kmitov,  cyklov =
cyklov =  kmitov.
kmitov.
Amplitúda všetkých cyklov je rovnaká, preto som ju neindexoval, ale položil rovnú konštante, ktorú som označil ako 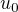 .
.
Frekvencia cyklov sa tiež nemení, teda každý z cyklov (kmitov) má rovnakú periódu. Takže môj pulz je vlastne sekvencia o dĺžke  harmonických kmitov rovnakej amplitúdy a frekvencie.
harmonických kmitov rovnakej amplitúdy a frekvencie.
Je to ako nastavenie parametrov pulzu na fuknčnom generátore - tiež si volíte amplitúdu, počet cyklov/kmitov a frekvenciu (príp. ešte aj počiatočnú fázu).
Snáď teraz je o niečo viac zrozumiteľné. Vtedy som bol inakšie ucho :D
Offline
#7 28. 08. 2018 00:53
Re: Piezokryštalický oscilátor budený napäťovým pulzom
↑ Ferdish:
Tak tomu tak nějak rozumím.
Ta frekvence pulzů odpovídá rezonanční frekvenci toho piezo-oscilátoru, nebo je někde mimo?
Těch pulzů je hodně (že by to skoro dosáhlo ustáleného stavu) nebo je jich jen pár (ve srovnání s dobou ustálení) ?
Ale vůbec nerozumím, co myslíš tou "celkovou amplitudou pulzu", co jsi zmiňoval v úvodním příspěvku. Co jsi vlastně potřeboval vypočítat ?
Offline
#8 28. 08. 2018 19:42
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Piezokryštalický oscilátor budený napäťovým pulzom
↑ MichalAld:
Frekvencia pulzov zodpovedá frekvencii piezo-oscilátora.
Počet pulzov je malý, rozhodne nedôjde k ustálenému stavu.
Čo sa týka tej celkovej amplitúdy, to bude zrejme moja chyba, ktorej som sa vtedy dopustil. Mala tam byť celková energia pulzu :)
No ako som už povedal vyššie - problém som už medzitým vyriešil, osobne nemám dôvod sa ním ďalej zaoberať.
Ak ťa však zaujal natoľko, že chceš v diskusii pokračovať, nedbám...
Offline
#9 28. 08. 2018 20:33
Re: Piezokryštalický oscilátor budený napäťovým pulzom
Pokud nedbáš...
Na začátku mi to přišlo snadné, ale celé to závisí na skutečném chování toho piezo-rezonátoru.
Pokud budeme uvažovat, že jde o systém druhého řádu, je řešení jednoduché.
Jenže otázka je, nakolik je takový předpoklad oprávněný. Protože třeba klasické "krystaly", co se používají ke stavbě oscilátorů, mají chování složitější.
Náhradní schema,
frekvenční charakteristika
Pokud jde ovšem o piezo-měnič na akustických frekvencích, tak se tam podle mě žádná paralelní rezonance neprojeví.
Offline
#10 29. 08. 2018 00:04
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Piezokryštalický oscilátor budený napäťovým pulzom
Nejak nerozumiem...ako môže energia budiaceho pulzu, ktorý ešte len do rezonátora posielam, závisieť od vlastností rezonátora?
Všetko ostatné za vetou "Mojim problémom je, že netuším ako vypočítať celkovú amplitúdu pulzu." môžeš kľudne ignorovať.
Vtedy som bol väčšie ucho než som teraz a doplietol som tam hrušky s jablkami. Zrejme aj preto mi vtedy nikto nevedel na túto otázku odpovedať :)
Offline
#11 29. 08. 2018 15:53
Re: Piezokryštalický oscilátor budený napäťovým pulzom
Pokud jde jen o energii budícího pulzu - v teorii signálů se za energii signálu 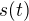 považuje prostě funkce
považuje prostě funkce 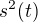 . Je to samozřejmě jen hustota energie (výkon), abychom dostali energii, museli bychom to zintegrovat, tedy
. Je to samozřejmě jen hustota energie (výkon), abychom dostali energii, museli bychom to zintegrovat, tedy 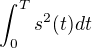 .
.
Pro sinusový signál to samozřejmě není nic jiného, než jeho efektivní hodnota krát čas (pokud je čas celistvým násobkem periody signálu).
Fyzikální energii to ovšem odpovídá jen za určitých okolností. Fyzikální vztah pro energii napěťového signálu je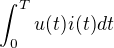
a teď závisí na vztahu mezi napětím a proudem. Dále bych mluvil jen o jednoducých lineárních případech, nebudu se zabývat variantou, že napětím napájíme třeba spínaný zdroj.
Pokud je vztah mezi napětím a proudem čistě lineární, tedy 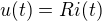 , dostaneme pro energii pulzu jednoduše
, dostaneme pro energii pulzu jednoduše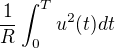
Z pohledu teorie signálů je ta konstanta 1/R nezajímavá (je to jen konstanta a nemá na nic dalšího vliv), pokud chceš ovšem spočítat fyzikální energii (v Joulech), tak je samozřejmě rozdíl, jestli to napětí "pouštíš" do rezistoru 1 Ohm, nebo 1 MOhm.
Dále - v obvodech, kde neuvažujeme rozložené parametry (jako třeba vedení, po kterém se pulz šíří nějakou rychlostí) moc nedává smysl mluvit o energii samotného pulzu, ale jen o energii, kterou do nějakého prvku předáme (nebo odebereme).
Pro případ jednoduché lineární závislosti mezi napětím a proudem (čistě ohmická, reálná zátěž) je tedy odevzdaná energie podle výše uvedeného vztahu - a odpovídá efektivní hodnotě napětí - která je takto vlastně definovaná.
Pokud ovšem proud obsahuje i složky závislé na derivaci (nebo integrálu) napětí, říkáme že zátěž obsahuje i reaktanční složku - a ta nám žádnou energii nespotřebovává. Část doby si ji "bere" a zbylou část "vrací".
Pokud má zátěž jak ohmickou, tak reaktanční zátěž, tak se oba efekty kombinují, zavádí se kvůli tomu tzv. činný a jalový výkon.
Offline
#12 29. 08. 2018 16:07 — Editoval MichalAld (29. 08. 2018 16:12)
Re: Piezokryštalický oscilátor budený napäťovým pulzom
Pokud jde o rezonanční obvod, je to všechno ještě trochu složitější.
Všechny ty úvahy o ohmické a reaktanční zátěži se týkají ustálených stavů.
V ustáleném stavu se rezonanční obvod pro signál jehož frekvence je stejná jako rezonanční frekvence obvodu chová jako čistě reálný odpor. S tím žádný problém není.
Jenže my neřešíme ustálený stav, řešíme krátký impulz (krátký ve srovnání s časovou konstantou tlumení rezonančního obvodu). A v tom případě se chová tak, že jeho výchylka (v našem případě proud) lineárně narůstá - s každám dalším pulzem našeho signálu signálu je o stejnou hodnotu větší. Samozřejmě - jen u ideálního rezonančního obvodu by to pokračovalo až do nekonečna. U reálného se nárust postupně zpomaluje (závisí to právě na časové konstantně toho tlumení) až se nakonec na nějaké hodnotě ustálí.
To, jaký bude nárust výchylky během každé periody - to závisí na hodnotách L a C našeho rezonančního obvodu. A já popravdě z hlavy nevím jak přesně a nechce se mi to teď hledat. Ale předpokládám, že to bude dle vztahu
protože ten vychází rozměrově v ohmech.
Takže čím vyšší bude tato hodnota, tím menší energii náš pulz do oscilátoru předá.
Samozřejmě to také lineárně závisí na amplitudě našeho signálu a počtu period (pokud je signál znatelně kratší než časová konstanta tlumení rezonančního obvodu).
Ovšem z hlavy si netroufnu říct, jestli se tam neobjeví nějaká další bezrozměrná konstanta blízká jedné.
Takže po složitých úvahách se dostáváme k celkem jednoduchému výsledku
N - počet "sinusovek"
T - perioda, doba jedné "sinusovky"
Uef - efektivní hodnota sinusového signálu,
Ač mluvíme o elektrickém rezonančním obvodu, platí to i pro mechanický. Jen místo L a C tam bude kombinace hmotnosti a tuhosti. Nevím ovšem, jak tuhle hodnotu určit, jinak než změřením.
A ještě jedna věc - předpokládá to použití ideálního zdroje napětí (bez vnitřního odporu). Jinak se nám tento odpor projeví jako dodatečné tlumení rezonančního obvodu. Další věc je, že přívodní vodiče mají i nějakou indukčnost nebo kapacitu - to vše nám rezonátor nějakým způsobem ovlivní. A samozřejmě je pak otázka, co myslíme tím napětím, jestli napětí naprázdno, nebo až po připojení.
A ještě jednou na závěr připomínám - u napětí v obvodech s dikrétními součástkami nemá význam hovořit o "energii signálu" či "energii puzlu" pokud jde o samotné napětí. Vždy musíme vzít v úvahu i proud - a ten může na napětí záviset obecně libovolně komplikovaným způsobem (nebo na něm nemusí záviset vůbec a může si "žít svým životem").
Offline
Stránky: 1
- Hlavní strana
- » Fyzika
- » Piezokryštalický oscilátor budený napäťovým pulzom (TOTO TÉMA JE VYŘEŠENÉ)