Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 13. 10. 2018 15:10
Re: Hádanka
↑ CUllblade:
Anebo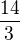 
. :-) Ctyrikrat horni minus petkrat levy plus petkrat pravy vrchol. To cele deleno tremi.
Offline
#5 13. 10. 2018 23:06
- check_drummer
- Příspěvky: 4952
- Reputace: 106
Re: Hádanka
Ahoj, vaše řešení postrádají symetričnost a vždy preferují nějaký specifický vrchol (vrcholy). Nabízím proto tento postup:
Sestrojme absolutní hodnoty rozdílů sousedních dvojic vrcholů, to opakujme iterativně tak dlouho, dokud některá z hodnot nebude 0. Označme jako x maximum z takto získané trojice a jako y počet kroků, které bylo potřeba provést. Potom je prostřední prvek trojúhelníku určen vztahem 4/3.x+2/3.y+2. (A tedy pro nezmámé číslo máme x=1,y=3 a tedy hledané číslo je 16/3.) A pokud je požadováno, aby prostřední číslo bylo vždy celé, tak nakonec provedeme ještě operaci dolní celá část.
Jestli je to špatně, tak sním svůj klobouk. (Pozn.: žádný nemám)
"Máte úhel beta." "No to nemám."
Offline
#6 14. 10. 2018 07:38
- misaH
- Příspěvky: 13459
Re: Hádanka
↑ check_drummer:
No. Ešte si snáď nejaký môžeš kúpiť, nie?
Offline