Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 10. 2018 16:17
analytická geometrie v rovině
Dobrý den, mohl by mi někdo prosím poradit s příkladem z analytické geometrie, vektory mi vůbec nejdou a sem v koncích.
Vím, že rovnoběžná bude tehdy, pokud normálnový vektor přímky p [v tomhle případě vektor (2, -1)] bude vektorem směrovým přímky druhé, např. q.
vzoreček na vzdálenost bodu a přímky znám taky: d=|ax1 + bx2 + c| /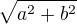
d se v tomhle případě rovná 3.
ale nenapadá mě jak určit to parametrické vyjádření.
Kdybych si zvolil nějaký bod A = [0,1] na přímce p a rovnoběžku hledal pro přímku 2x - y + c = 0
Vzdálenost bodu A od přímky by byla 3.
konstantu c bych vypočítal ze vzorečku: to mi vyšlo ale divně: 
Vůbec netuším jak an to, kdyby mi někdo mohl nějak poradit byl bych mu vděčný. Předem děkuji za jakoukoliv odpověď.
Offline
#2 16. 10. 2018 16:40 — Editoval Jj (16. 10. 2018 16:56)
Re: analytická geometrie v rovině
↑ NeuRotiCk:
Zdravím.
Vím, že rovnoběžná bude tehdy, pokud normálnový vektor přímky p [v tomhle případě vektor (2, -1)] bude vektorem směrovým přímky druhé, např. q.
Takto to zrovna není, ale teď to nechme.
Rovnoběžku k p: 2x - y - 4 = 0 můžete hledat jak uvádíte, jen bod A musí ležet na přímce p, a to u bodu A(0,1) neplatí (souřadnice bodu nenulují její rovnici).
Takže lépe zvolit bod A a je možno pokračovat.
Edit: Ještě dodám, pro c je třeba najít dvě řešení. A divných výsledků se až tak nebojte - důležité je, aby byla správná vzdálenost přímek.
Pokud se tedy nemýlím.
Offline
#3 16. 10. 2018 17:31
Re: analytická geometrie v rovině
Dobrá tedy, tak si zvolím bod A = [2,0].
Budu to řešit zase pro rovnici 2x - y + c= 0
vypočítám c ze vzorečku 
ax1 = 2; by1 = 0
a = 2; b= -1
d= 3
takže mi vyjde, že 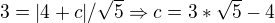
ale stejně nechápu proč sem to spočítal a co mi to dá, už mi z toho běhá hlava kolem :D
Offline
#5 16. 10. 2018 17:54
Re: analytická geometrie v rovině
Řešení by byly dvě, +- to mi je jasný, zapomněl sem to napsat.
Stačilo by, kdybych u té rovnice 2x - y +4 = 0 zjistil směrový vektor, což by v tomhle případě bylo (1,2) ne? a potom pomocí toho mého bodu A bych sestavil parametrické vyjádření přímky.
Což by následně vypadalo:
x = 2 + t
y = 2t
Offline
#6 16. 10. 2018 17:59 — Editoval misaH (16. 10. 2018 18:00)
- misaH
- Příspěvky: 13460
Re: analytická geometrie v rovině
↑ NeuRotiCk:
Ale keď ten bod A leží na pôvodnej priamke, určite neleží na priamke, ktorá je od pôvodnej 3 cm ďaleko. Preto sa nedá bod A použiť na parametrické vyjadrenie rovnobežky.
Veď si to nakresli...
Potrebuješ k smerovému vektoru rovnobežky (máš ho dobre) ešte 2 body, 1 "nad" danou priamkou a druhý "pod" ňou také, že ich vzdialenosť od danej priamky je 3 (cm).
Offline
#7 16. 10. 2018 18:03 Příspěvek uživatele Jj byl skryt uživatelem Jj. Důvod: Nestihl, aspoň zdravím :)
#8 16. 10. 2018 18:06 — Editoval misaH (16. 10. 2018 18:19)
- misaH
- Příspěvky: 13460
Re: analytická geometrie v rovině
Určite si načrtni obrázok + rovnobežky.
1. napíš "vzorec" pre vzdialenosť bodu od priamky, polož vzdialenosť rovnú 3
2. súradnice hľadaného bodu označ napríklad x1, y1
3. zvoľ si (podľa mňa) a dosaď ľubovoľné x1 (je jedno, ktorý bod rovnobežky použiješ)
4. vyrieš rovnicu s absolútnou hodnotou - dostaneš 2 hodnoty y1
5. najprv 1 bod x1, y1 použi na parametrické vyjadrenie rovnobežky a potom aj druhý bod.
Úloha má nekonečne veľa podôb riešenia...
Offline
