Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Určování definičního oboru (TOTO TÉMA JE VYŘEŠENÉ)
#1 19. 10. 2018 11:50
Určování definičního oboru
Ahoj, potřeboval bych poradit s následujícímu příklady.
1) ![kopírovat do textarea $f(x)=\frac{x(x^{2}+5)}{tg(\frac{1}{x^{7}})\cdot ln\sqrt[3]{x^{2}}}$](/mathtex/86/86e7b4e6d03ffd64c8be2dcf46eed152.gif) Určit definiční obor.
Určit definiční obor.
Řešení:
1.1 ![kopírovat do textarea ${tg}x\not=0 \Rightarrow \frac{1}{x^{7}}\not=k\frac{\pi }{2} \Rightarrow x\not= \frac{\sqrt[7]{2k^{6}\pi ^{6}}}{k\pi}$](/mathtex/68/68014134daf78f20bfc26500948f9e6a.gif)

1.2 ![kopírovat do textarea $\ln x \not= 0 \Rightarrow \sqrt[3]{x^{2}} \not= 1 \Rightarrow {x} \not= \pm 1$](/mathtex/fd/fdf102335f6e3758bb25bd11155b3605.gif)
1.3 ![kopírovat do textarea $\sqrt[3]{x^{2}}>0\Rightarrow x \not= 0$](/mathtex/42/42f503dbd1f576275b402549b9c40a01.gif)
Předpokládám, že podmínky jsem určil správně (přesto prosím o kontrolu). Jak teď rozumně zapsat výsledný definiční obor?
2)  Taktéž určit definiční obor.
Taktéž určit definiční obor.
2.1  Nerovnici jsem zlogaritmoval a dospěl jsem zde.
Nerovnici jsem zlogaritmoval a dospěl jsem zde.
Nakonec mi z toho vyšlo: 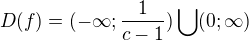

Podle Wolframu je už i ta nerovnice nesprávná (proč?).
3) Obecný dotaz - např. zlogaritmování nerovnice mění nerovnost pokud je logaritmus klesající funkce? Pokud ano, jak je to v případě funkcí, které nejsou ani rostoucí ani klesající, např. tangens?
Offline
- (téma jako vyřešené označil(a) Kleanthés)
#2 19. 10. 2018 12:13 — Editoval krakonoš (19. 10. 2018 13:11)
Re: Určování definičního oboru
.V 1.3 jde logaritmus do minus nekonecna,kdyz jdes k nule zprava.Tam nedelis nulou.Pardon. Spletly se mi 2 radky. Tam vlastne musime uvazovat log kladneho cisla.
Z def oboru R bych vyjmula hodnoty -1;0;1;k.pi/2 pro k rovno 1,2,3.....
U toho bodu 2.1 je jakymsi zlomem bod -1.Nutno si uvedomit,ze abs hodnota i klesa,proto se mi nezda to logaritmovani.. Tady se budou muset rozlisit intervaly minus nekonecno az minus jedna.Dale minus jedna az nula a nula az nekonecno Odstranit si absol hodnotu a resit nerovnice. Na intervalu -1;0 bude asi zlom,kde neni definovana.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#3 19. 10. 2018 13:28 — Editoval Rumburak (19. 10. 2018 13:45)
Re: Určování definičního oboru
↑ Kleanthés:
Ahoj.
Určit definiční obor funkce znamená vyhnout se případům, kdy by funkce nebyla definována.
Například u funkce 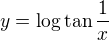 ("tan" znamená "tangens") je potřeba klást podmínky
("tan" znamená "tangens") je potřeba klást podmínky
(1)  , aby měl smysl zlomek
, aby měl smysl zlomek  (jak víme, nulou dělit nelze),
(jak víme, nulou dělit nelze),
dále
(2) 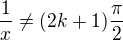 , kde
, kde  je celé číslo (viz definiční obor funkce tangens),
je celé číslo (viz definiční obor funkce tangens),
a konečně
(3)  (viz definiční obor logaritmické funkce).
(viz definiční obor logaritmické funkce).
Obvykle je požadováno explite vyjádřit "průnik" takových podmínek formulí tvaru
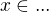 nebo aspoň
nebo aspoň 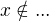 .
.
Offline
#4 19. 10. 2018 13:45
Re: Určování definičního oboru
↑ Rumburak:
Ano, to všechno já samozřejmě vím (viz mé příklady a řešení). Prosím o kontrolu mého řešení.
Offline
#5 19. 10. 2018 13:47
Re: Určování definičního oboru
↑ krakonoš:
Já právě nevím, jak funguje to zlogaritmování - domníval jsem se, že záleží na monotonii logaritmu, ne funkce, kterou chci zlogaritmovat. Jak to tedy je?
Offline
#6 19. 10. 2018 13:55 — Editoval krakonoš (19. 10. 2018 14:07)
Re: Určování definičního oboru
Pokud bude a mensi nez b ,mohu na ne pouzit rostouci funkci napr log a zustane mensi nez log b.Predstav si,ze pouzijes na a mene nez b exponencielu. Tim ale napr pro a rovno jedne a b rovno stu razantne zvysis rozdil . Puvodne byl rozdil 99, a vem si jaky bude nyni. Pokud bys na a mene nez b pouzil klesajici fci napr minus e nax. Nerovnost nebude zachovana a stane se z ni pravy opak pri urcitych volbach a b.Takze se muze stat,ze nekde se jeste zachova stejn ne pri blizkych a b,jinde uz ne.....
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#7 19. 10. 2018 15:01
Re: Určování definičního oboru
↑ Kleanthés:
K úloze 1:
Měníš význam proměnné  , což je chyba. Například: v předpisu funkce
, což je chyba. Například: v předpisu funkce  se výraz
se výraz 
nevyskytuje, proto nás jeho definice ani hodnota zajímat nemusí. Místo toho nás ale musí zajímat
výraz 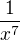 :
:
- musí být definován, což znamená podmínku  ,
,
- musí padnout do definičního oboru funkce tangens, což znamená podmínku  ,
,  celé,
celé,
- musí být splněno 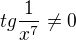 , aby jmenovatel "hlavního" zlomku v předpisu funkce
, aby jmenovatel "hlavního" zlomku v předpisu funkce  byl nenulový,
byl nenulový,
což znamená podmínku 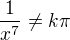 ,
,  celé.
celé.
Dál jsem nic nekontroloval - předpokládám, že můj dosavadní rozbor by mohl stačit.
Offline
#8 19. 10. 2018 15:09
Re: Určování definičního oboru
↑ krakonoš:
Aha. To mi právě ještě nikdo nevysvětlil, ale už tomu rozumím. Jestli a < b, pak i log a < log b. Pokud na obě strany aplikujeme rostoucí funkci, nerovnost se zachová. Pokud na obě strany aplikujeme klesající funkci, nerovnost se musí obrátit; jestli a < b, pak 0.5^a > 0.5^b (ovšem ne jen při určitých volbách, ale při všech, neboť 0.5^x je klesající na celém svém definičním oboru). Proto obecně nemůžu aplikovat na nerovnost třeba funkci tangens, neboť ta není ryze monotónní. Dále, jestli x < 5, pak musí být i log x < log 5, neboť logaritmus je v tomto případě rostoucí funkce. Stejné by to bylo i pro x^6 > x^5.
Obecně tedy není problém aplikovat ryze monotónní funkci na ryze monotónní funkci. V opačném případě musíme příklad vyřešit jinak. Rozumím tomu správně?
Offline
#9 19. 10. 2018 15:22
Re: Určování definičního oboru
↑ Rumburak:
To je přeci jasné, ale sám jsi předtím napsal, že definiční obor se zadává ve tvaru x náleží... , nikoliv 1/x^7 náleží...
Cituji:
"Obvykle je požadováno explite vyjádřit "průnik" takových podmínek formulí tvaru"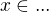 nebo aspoň
nebo aspoň 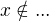 .
.
Offline
#10 19. 10. 2018 15:56 — Editoval krakonoš (19. 10. 2018 15:58)
Re: Určování definičního oboru
↑ Kleanthés:Ano,kdyz aplikujes funkci xnadruhou pro kladna a,b .Zustane nerovnost zachovana. Pro zaporna ale docilis praveho opaku. On vlastne ten problem uzce souvisi s derivaci,jeji znamenko rozhodne,zda fce roste nebo klesa ( pochopitelne spojitych fci co maji derivaci).To je vlastne podil rozdilu funkcnich hodnot a rozdilu bodu na ose x.
Co se tyce toho dalsiho prikladu.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#11 19. 10. 2018 17:43 — Editoval misaH (19. 10. 2018 17:45)
- misaH
- Příspěvky: 13459
Re: Určování definičního oboru
Měníš význam proměnné
, což je chyba.
Rumburak má pravdu - nemôžeš miešať v 1 zápise rôzne významy premennej x
Buď je argument x alebo ten zlomok, na toto si dávaj veľký pozor.
Keby si napísal, že hodnota funkcie tangens v menovateli nesmie byť 0, bolo by to v poriadku. Keď napíšeš miesto toho niečo o tg x, už je to chyba a dosť veľká...
Offline
#12 19. 10. 2018 17:56 — Editoval Kleanthés (19. 10. 2018 18:15)
Re: Určování definičního oboru
↑ krakonoš:
V druhém příkladu jsem postupoval tak, že jsem si rozdělil osu reálných čísel do dvou intervalů, a tak se zbavil absolutní hodnoty. Až poté jsem nerovnice zlogaritmoval a dostal se k výsledku  . Předtím jsem udělal drobnou chybu a výsledek mi vyšel jiný. Jde o to, že nakonec dostanu nerovnici ve tvaru a^x > b^x, tu jinak nedokáži vyřešit bez zlogaritmování.
. Předtím jsem udělal drobnou chybu a výsledek mi vyšel jiný. Jde o to, že nakonec dostanu nerovnici ve tvaru a^x > b^x, tu jinak nedokáži vyřešit bez zlogaritmování.
Offline
#14 19. 10. 2018 18:06 — Editoval misaH (19. 10. 2018 20:53) Příspěvek uživatele misaH byl skryt uživatelem misaH.
#15 19. 10. 2018 18:13 — Editoval misaH (19. 10. 2018 18:16)
- misaH
- Příspěvky: 13459
Re: Určování definičního oboru
↑ Kleanthés:
Ahoj - no, úlohu vnímam len okrajovo, do hĺbky sa mi v tom patlať nechce, ešte by som vyrobila nejakú chybu...
ale verím, že niekto ti pomôže.
A je lepšie (podľa pravidiel) dávať každú úlohu do vlastnej témy, aby nevznikol chaos v odpovediach...
Offline
#16 19. 10. 2018 18:23
Re: Určování definičního oboru
↑ misaH:
Udělal jsem formální chybu, děkuji za upozornění. Neuvědomil jsem si to. Pointa mého dotazu k příkladu 1 tkvěla v tom, že si nevzpomínám, jak se zapisuje "velké sjednocení", zda je možné to zapsat třeba takto:![kopírovat do textarea $x\in \mathbb{R}\setminus \{-1; 0; 1\} \setminus \bigcup_{k\in \mathbb{Z}}^{{}} \frac{ \sqrt[7]{2k^{6}\pi ^{6}} }{k\pi }$](/mathtex/4f/4f0ed3a406e750e0a89fe0412a58f794.gif)
Podmínky je třeba nějak sjednotit... Taky jsem upravil ten zlomek, aby nebyla odmocnina ve jmenovateli.
Teď taky vidím další chybku. Má tam být 
Offline
#17 19. 10. 2018 18:35
Re: Určování definičního oboru
Pro x rovno vetsi nez -1 prejde abs hodnota v x plus 1.Vyraz pod odmocninou musi byt roven nebo vetsi nez nula.Postupne se dostaneme k nerovnici 4 rovno vetsi nez (3/4) umocneno na x (klesajici epon funkce) Nakresli si tyto dve funce a spocti,kde je ta hranice. Mel by ti vyjit interval
max(-1;log4/log(3/4));nekonecno.
Podobne postupuj pro x mensi nez -1.
Zde se porovnava konst funkce 1/4 rovno vetsi nez 12 umocneno na x.Opet se vysleduje hranice,kdy jde funkce pod 1/4 a zaroven je x mensi nez -1. Tady by to mel byt intetval -nekonecno;min(-1;log(1/4)/log12).
To min a max je tam protoze nemam tabulky a nejsem schopna to porovnat.
Takhle to vidim ja. Jesti jsem se nespletla ve vypoctu.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#18 19. 10. 2018 19:01 — Editoval misaH (19. 10. 2018 20:54) Příspěvek uživatele misaH byl skryt uživatelem misaH.
#19 19. 10. 2018 20:08
#20 19. 10. 2018 20:15
Re: Určování definičního oboru
↑ misaH:
Tohle je marné.
1) Výsledek mi vyšel naprosto stejně jako Rumburakovi, copak to nevidíš? Podmínky jsou správně (až na tu formální chybu, měl jsem místo tg x => ... použít třeba tg a => ...). Zbytek není divný, jsou to obyčejné algebraické úpravy.
2) Pokud se ptám na X, tak opravdu nechci slyšet odpověď na Y.
Děkuji alespoň za snahu.
Offline
#21 19. 10. 2018 20:23 — Editoval misaH (19. 10. 2018 20:55) Příspěvek uživatele misaH byl skryt uživatelem misaH.
#23 20. 10. 2018 17:38
Re: Určování definičního oboru
↑ Kleanthés:
To jsme si nerozuměli. Ve tvaru 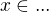 resp.
resp. 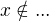
se uvádí až konečný výsledek.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Určování definičního oboru (TOTO TÉMA JE VYŘEŠENÉ)

![kopírovat do textarea $x\in \mathbb{R}\setminus \{-1; 0; 1\} \setminus \bigcup_{k\in \mathbb{Z}}^{{}} \frac{ \sqrt[7]{2k^{6}\pi ^{6}} }{k\pi }$](/mathtex/2e/2eaa824cca38bca94b6e9a10fd44facb.gif)