Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 10. 2018 20:33 — Editoval ebabuli (26. 10. 2018 20:34)
kuželosečky 6
TAK JDU OPĚT PRO RADU. Mám příklad napište rovnici kružnice, která prochází bodem A a dotýká se obou souřadných os. bod A(3,-6) výsledek: 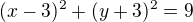 nebo
nebo 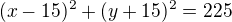
a pocitala jsem takhle z obdobneho prikladu kde bod A(8,9) kdy jsou dve moznosti S(X,X) nebo S(X,-X)...kdyz si to nakreslim zjistila jsem ze u bodu A(8,9) je první kvadrant tedy S(X,X) a ze bod A(3,-6) je ve ctvrtem kvadrantu tedy S(X,-X)...snazila jsem se obdobne pouzit vzorec kdy Sy=Sx=SA a pocitat dle  kde mi to u kladných souřadnic bodu A vyšlo...jak to pozměnit, aby mi to vyslo kdyz bod nemá kladné souřadnice ale právě ty záporné (3,-6) dekuji za rady
kde mi to u kladných souřadnic bodu A vyšlo...jak to pozměnit, aby mi to vyslo kdyz bod nemá kladné souřadnice ale právě ty záporné (3,-6) dekuji za rady
Offline
- (téma jako vyřešené označil(a) ebabuli)
#2 26. 10. 2018 21:01 — Editoval gadgetka (26. 10. 2018 21:03)
Re: kuželosečky 6
Ahoj, kružnice, která se dotýká obou souřadných os má střed  o souřadnicích
o souřadnicích ![kopírovat do textarea $[r; r]$](/mathtex/a1/a1357ce81ae566fe00a213a33b830529.gif) . :)
. :)
Tedy: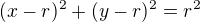
Stačí dosadit souřadnice bodu, kterým prochází. A tím dopočítáš poloměr. :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#3 26. 10. 2018 21:03 — Editoval misaH (26. 10. 2018 21:04)
- misaH
- Příspěvky: 13460
Re: kuželosečky 6
↑ ebabuli:
Ahoj.
Ty si tie úlohy kreslíš?
Je to absolútny základ... neuč sa príklady, uč sa systém, princíp.
Čo znamenajú písmenká v nasledujúcom riadku?
Offline
#4 26. 10. 2018 21:04
#5 26. 10. 2018 21:16 — Editoval misaH (26. 10. 2018 21:20)
- misaH
- Příspěvky: 13460
Re: kuželosečky 6
↑ ebabuli:
Že v rovnici kružnice miesto súradníc stredu dosadíš r miesto ixovej a -r miesto ypsilonovej ( v tomto máš pravdu :-) ).
A keď bod A leží na kružnici, miesto x v rovnici kružnice napíšeš jeho x a miesto y v rovnici dosadíš jeho y.
Vznikne jedna (kvadratická) rovnica s neznámou r.
Naozaj by si si to všetko mala kresliť - všetko sa "naučiť" cez "vzorce" nedá.
Offline
#7 26. 10. 2018 21:59
Re: kuželosečky 6
↑ ebabuli:
Zdravím,
začni tím, že do soustavy souřadnic u umístíš bod A(3,-6). Kde musí ležet kružnice, aby se dotýkala obou os a procházela bodem A? Z NÁČRTKU bude zřejmé, že musí ležet ve 4.kvadrantu, tudíž střed je ![kopírovat do textarea $S[r,-r]$](/mathtex/11/115823331def7023af66d37c01e33d68.gif) , jak jsi podotkla sama. Proto rovnice k řešení je
, jak jsi podotkla sama. Proto rovnice k řešení je 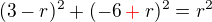
Offline
#8 26. 10. 2018 22:01 — Editoval misaH (26. 10. 2018 22:17)
- misaH
- Příspěvky: 13460
Re: kuželosečky 6
↑ ebabuli:
No - mala si pravdu, že súradnice stredu sú potom r a -r
Rovnica: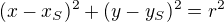
Potom:
Offline

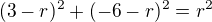 ??? protože tak jsem to počítala a to nevychází jeden kořen je 3 cože je dobře, ale druhý -9 :(
??? protože tak jsem to počítala a to nevychází jeden kořen je 3 cože je dobře, ale druhý -9 :(