Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 10. 2018 18:47
kuželosečky-nerovnice
Zdravím ;) Potřebovala bych radu s trošku netradičním příkladem. Nepomáhá mi ani náčrtek, ani dosazování.
Určete množinu bodů M(x,y), které splňují nerovnici  a graficky tuto množinu bodů znázorněte. výsledek je mezikruží
a graficky tuto množinu bodů znázorněte. výsledek je mezikruží
napadlo mě vyřešit S a ten by měl být (2,-3) no co dál s ním nevím :)
určila jsem si, že rozsah x a y musí být max 16-25 a zkusila jsem tedy dosazovat náhpodně X a pak vypočítat y a následně to zakreslit, ale výsledkem by byla přímka, protože y by bylo vždy 1 :(
poradí mi někdo prosím ;)
Offline
- (téma jako vyřešené označil(a) ebabuli)
#2 28. 10. 2018 18:53
Re: kuželosečky-nerovnice
↑ ebabuli:
Ahoj, zkus si nakreslit dve kruznice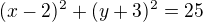
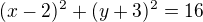
a trochu zapremejslet ;-)
Offline
#4 28. 10. 2018 19:15 — Editoval vlado_bb (28. 10. 2018 19:16)
Re: kuželosečky-nerovnice
↑ ebabuli: Zapisat sa to da takto:
To co pises potom su nezmysly, prienik je operacia medzi mnozinami a nie nerovnostami.
Offline
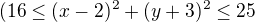 )=
)=

 takže poloměry jsou 5 a 4
takže poloměry jsou 5 a 4