Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 11. 2018 00:07
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
náhodná veličina
Ahoj,
mám úlohu, kde mám problém s výpočtem.
Házíme 2 kostkami - červenou a modrou. Nechť náhodná veličina odpovídá většímu z obou čísel. (Pokud jsou obě hodnoty stejné, nabývá X tomuto číslu). Určete její rozdělení, střední hodnotu a rozptyl.
Tak předpokládám, že půjde o binomické rozdělení. Potom n=2, ale bohužel nějak tápu v pravděpodobnosti. Ví někdo a pomůže?
Offline
#2 05. 11. 2018 00:31
Re: náhodná veličina
↑ xstudentíkx:
Ahoj, tak co začít s určením pravděpodobností pro 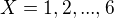 ?
?
Čemu se rovná pravděpodobnost, že X bude rovna jedné? 
Offline
#3 05. 11. 2018 00:36
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: náhodná veličina
↑ Pritt:
Děkuji za reakci. Tak pravděpodobnost, že padne jakékoli číslo na kostce je 1/6. Že padne například 1 a 1 je 1/36. Že padne 1 a 2 je rovněž 1/36,.... Nevím jak tam zakomponovat "Nechť náhodná veličina odpovídá většímu z obou čísel".
Offline
#4 05. 11. 2018 00:38
Re: náhodná veličina
↑ xstudentíkx:
No takže pokud X = 1, tak to je jen v případě, že padne 1 a 1. Protože jinak X bude něco většího.
Pokud X = 2, tak je to v případech, že padne 1 2, 2 1, 2 2, atd.
Offline
#5 05. 11. 2018 10:28
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: náhodná veličina
↑ Pritt:
Takže potom X = 3, bude 1 3, 3 1, 3 2, 2 3, 3 3
Takto pro všechna další X a střední hodnotu potom teda zjistím přes vzorec 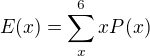 ?
?
Offline
