Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 30. 10. 2018 21:20
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: series
Hi, try partial fractions.
"Máte úhel beta." "No to nemám."
Offline
#3 01. 11. 2018 11:26
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: series
Thanks Check_drummer.please explain me . I am not getting
Offline
#4 02. 11. 2018 15:35
#5 05. 11. 2018 02:29
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: series
Thanks check_drummer. but from here we have calculate 
But how can i find  Thanks
Thanks
Offline
#6 05. 11. 2018 15:32
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: series
↑ stuart clark:
It is telescoping sum, you only need  but hopefully it can be neglected because you need only the whole part of S. But this should be proved...
but hopefully it can be neglected because you need only the whole part of S. But this should be proved...
"Máte úhel beta." "No to nemám."
Offline
#7 05. 11. 2018 16:30
Re: series
↑ check_drummer:
Is it realy telescoping sum? The sum
is different from the sum
Observation:
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#8 06. 11. 2018 02:01
Re: series
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#9 06. 11. 2018 22:31
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: series
Pavel napsal(a):
↑ check_drummer:
Is it realy telescoping sum? The sum
is different from the sum
Of course... Thank you for the comment.
"Máte úhel beta." "No to nemám."
Offline
 given as
given as  and
and  .
. . Then
. Then  is
is
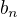 is increasing rapidly similarly as the sequence
is increasing rapidly similarly as the sequence  ,
,  . It is enough to sum the first 10 terms, since
. It is enough to sum the first 10 terms, since  . In other words, it seems that
. In other words, it seems that




