Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » Májové googlení (TOTO TÉMA JE VYŘEŠENÉ)
#1 26. 05. 2009 00:34 — Editoval Kondr (28. 05. 2009 11:05)
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Májové googlení
EDIT: přidána úloha b), úloha a) byla lehčí než jsem myslel.
Možná to znáte, možná najdete na netu, ale je to zajímavé ...
a) Najděte příklad konečně generované grupy G a její podgrupy H tak, aby H nebyla s G totožná, ale aby H a G byly izomorfní.
b) Najděte příklad konečně generované grupy G a její podgrupy H tak, aby H nebyla s G totožná, ale aby  a G byly izomorfní pro nějaké n>1 nebo ukažte, že taková neexistuje.
a G byly izomorfní pro nějaké n>1 nebo ukažte, že taková neexistuje.
c) Najděte příklad grupy G a její podgrupy H tak, aby  a G byly izomorfní pro nějaké n>1.
a G byly izomorfní pro nějaké n>1.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#3 26. 05. 2009 10:29
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Májové googlení
↑ Rumburak:Výborně. Úloha byla inspirována jednou konkrétní pěknou grupou a koukám, že k oddělení "zrna od plev" je potřeba trochu silnější vlastnost. Ikdyž možná ani ta nebude stačit :)
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#5 26. 05. 2009 11:45
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Májové googlení
↑ Rumburak: Pozadí problému je takové, že asi před čtrnácti dny do Brna přiletěl Benjamin Steinberg a měl tu krátký cyklus přednášek "Groups generated by automata". Dá se toho o nich dost najít na webu, ale shrnu to: představme si konečný automat, který načítá z jedné pásky a s každým přechodem ze stavu do stavu zapíše jeden symbol na druhou pásku. Takový automat tedy z jedné nekonečné posloupnosti znaků vyrobí jinou. Automat s daným vstupním stavem je proto konečným popisem nějaké grupy permutací množiny nekonečných řetězců. Grupa generovaná automatem je grupa generovaná permutacemi, které odpovídají jednotlivým počátečním stavům. Dá se sestavit dvoustavový automat, který se pro jeden počáteční stav chová jako identita a pro druhý jako přičítání jedničky k binárně zapsaným řetězcům (psaným naopak). Grupa, kterou generuje, je izomorfní se 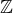 . Každý automat nad n-prvkovou abecedou generuje podgrupu grupy T_n všech permutací na nekonečných řetězcích nad danou abecedou. Snadno rozmyslíme, že T_n je izomorfní s (T_n)^n (tedy T_n splňuje b) až na to konečné generování). Po chvilce hledání objevíme i automat, který generuje její dost velkou podgrupu na to, aby měla požadovanou vlastnost.
. Každý automat nad n-prvkovou abecedou generuje podgrupu grupy T_n všech permutací na nekonečných řetězcích nad danou abecedou. Snadno rozmyslíme, že T_n je izomorfní s (T_n)^n (tedy T_n splňuje b) až na to konečné generování). Po chvilce hledání objevíme i automat, který generuje její dost velkou podgrupu na to, aby měla požadovanou vlastnost.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#6 27. 05. 2009 10:11 — Editoval Rumburak (28. 05. 2009 09:01)
Re: Májové googlení
↑ Kondr:
K úloze (b):
Krom toho, že nevím nic o automatech, mi není zcela jasná ani symbolika, ač pro znalce snad běžná.
1. Předpokládám správně, že ve struktuře 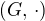 je pod
je pod  míněno
míněno 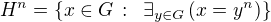 ?
?
2. Pokud ano, nemělo by se o grupě 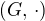 předpokládat, že je komutativní, aby
předpokládat, že je komutativní, aby  byla její podgrupou (speciálně aby byla uzavřená na součin) ?
byla její podgrupou (speciálně aby byla uzavřená na součin) ?
V případě, že odpověď na první otázku je kladná, pak myslím, že ani úloha (b) není těžká :
G - Aditivní grupa celých čísel,
H = G ,
potom 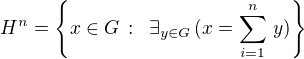 , kde mohu klást
, kde mohu klást 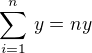 , takže
, takže  je aditivní grupa celých čísel dělitelných číslem n,
je aditivní grupa celých čísel dělitelných číslem n,
která je opět jako v případě (a) podgrupou v G isomorfní s G.
Ale je možné, že jsem úplně vedle, obecnou algebru jsem už dlouho neviděl ...
EDIT 1. Přehlédl jsem podmínku, že H má být vlastní podgrupou. Ale to asi půjde snadno zařídit , když místo H = G položím  , a tedy
, a tedy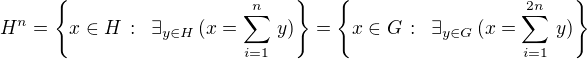 .
.
EDIT 2. K mé otázce 2: Uvědomuji si, že grupa mající pouze jeden generátor, je komutativní.
Dále se domnívám, že a) všechy grupy s jedním generátotem, které nejsou cyklické, jsou isomorfní,
b) dvě grupy, z nichž každá je s jedním generátorem a cyklická, jsöu isomorfní právě tehdy, jsou-li téhož řádu.
Že cyklická grupa nemůže být isomorfní s necyklickou, je zřejmé.
Určitě jsem neobjevil Ameriku, jen si tak pro sebe opakuji a ujasňuji ...
Offline
#7 28. 05. 2009 11:05
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Májové googlení
↑ Rumburak:Máš pravdu, značení H^n není jednoznačné. Měl jsem na mysli  , s operací
, s operací  prováděnou po složkách. Nicméně si sypu popel na hlavu, zadání jsem zmastil. Vycházel jsem ze svých poznámek z přednášky a v těch jsem vyrobil nějaký zmatek: T_n je opravdu izomorfni s (T_n)^n, ale nevím, kde jsem přišel na to, že by tuto vlastnost měly mít i nějaké její podgrupy. Ty určitě mají vlastnost popsanou v a) ale o b) začínám pochybovat.
prováděnou po složkách. Nicméně si sypu popel na hlavu, zadání jsem zmastil. Vycházel jsem ze svých poznámek z přednášky a v těch jsem vyrobil nějaký zmatek: T_n je opravdu izomorfni s (T_n)^n, ale nevím, kde jsem přišel na to, že by tuto vlastnost měly mít i nějaké její podgrupy. Ty určitě mají vlastnost popsanou v a) ale o b) začínám pochybovat.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » Májové googlení (TOTO TÉMA JE VYŘEŠENÉ)