Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita, urči reálný parametr tak, aby platilo (TOTO TÉMA JE VYŘEŠENÉ)
#1 09. 11. 2018 11:20 — Editoval AterCZ (09. 11. 2018 11:22)
Limita, urči reálný parametr tak, aby platilo
Ahoj,
mohu poprosit o pomoc s tímto typem příkladu? Existuje obecný postup?
1) 
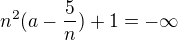
Tady jsem si řekl, že stačí, aby  bylo záporné číslo a nerovnalo se
bylo záporné číslo a nerovnalo se  . Tudíž
. Tudíž  . Podle výsledků ale i
. Podle výsledků ale i  je řešením..
je řešením..
2) 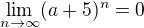
Řekl jsem si, že 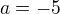 . Řešením je ale interval
. Řešením je ale interval 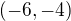 .. Chápu to správně, že
.. Chápu to správně, že  ,
,  se blíží k 0?
se blíží k 0?
3) 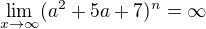
A tady si vůbec nevím rady, zkusil jsem jen vytknout.
Řešením je 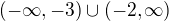
Offline
- (téma jako vyřešené označil(a) AterCZ)
#2 09. 11. 2018 11:37 — Editoval Rumburak (09. 11. 2018 12:31)
Re: Limita, urči reálný parametr tak, aby platilo
Ahoj.
Ad 1) Je to lehké, když si uvědomíme, jak vypadá průběh (graf) funkce 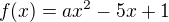
v závislosti na parametru  . Ano, i 0 je řešením.
. Ano, i 0 je řešením.
Ad 2) Jde o geometrickou posloupnost o kvocientu  .
.
Ad 3) Opět jde o geometrickou poslouonost - tentokrát s kvocientem  .
.
Offline
#4 09. 11. 2018 12:27
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita, urči reálný parametr tak, aby platilo (TOTO TÉMA JE VYŘEŠENÉ)

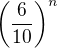 ak sa n blíži k nekonečnu sa samozrejme blíži 0
ak sa n blíži k nekonečnu sa samozrejme blíži 0