Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Postup řešení integrace složitějšího součinu
#1 14. 11. 2018 12:21
- adamatematika
- Zelenáč

- Příspěvky: 7
- Škola: vut fast
- Reputace: 0
Postup řešení integrace složitějšího součinu
Prosím nevím si rady s postupem nasledné integrace 
Děkuji
MATEMATIKADAM
Offline
#2 14. 11. 2018 12:27
Re: Postup řešení integrace složitějšího součinu
↑ adamatematika: Pod odmocninou treba scitat a dalej je to uz zrejme jasne.
Offline
#3 14. 11. 2018 12:28
Re: Postup řešení integrace složitějšího součinu
Ahoj ↑ adamatematika:,
Navod
Poloz u=x^2+1.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 14. 11. 2018 12:30
- adamatematika
- Zelenáč

- Příspěvky: 7
- Škola: vut fast
- Reputace: 0
Re: Postup řešení integrace složitějšího součinu
↑ vlado_bb:
Pod odmocninou jsem schopen sečist ale dalé mi to nejí zrejme jasné nemužete přibližit diky
MATEMATIKADAM
Offline
#5 14. 11. 2018 12:35
- adamatematika
- Zelenáč

- Příspěvky: 7
- Škola: vut fast
- Reputace: 0
Re: Postup řešení integrace složitějšího součinu
↑ vanok:
děkuji, pokusil jsem zkusit tuto cestu substituce ale bohuzel se nemohu dostat k vysledku
MATEMATIKADAM
Offline
#6 14. 11. 2018 12:43
Re: Postup řešení integrace složitějšího součinu
↑ adamatematika: Tak napis svoj postup, uvidime, pokial si sa dostal.
Offline
#7 14. 11. 2018 12:50
- adamatematika
- Zelenáč

- Příspěvky: 7
- Škola: vut fast
- Reputace: 0
Re: Postup řešení integrace složitějšího součinu
↑ vlado_bb:
dobre tady to je provedl jsem substituci
MATEMATIKADAM
Offline
#8 14. 11. 2018 12:53
Re: Postup řešení integrace složitějšího součinu
↑ adamatematika: Odmocni najprv  v menovateli.
v menovateli.
Offline
#9 14. 11. 2018 12:59
- adamatematika
- Zelenáč

- Příspěvky: 7
- Škola: vut fast
- Reputace: 0
Re: Postup řešení integrace složitějšího součinu
↑ vlado_bb:
ano ted je to asi zrejmejsí bohužel netuším jak vhodně substituovat abych se zbavil x-sů
MATEMATIKADAM
Offline
#10 14. 11. 2018 13:06
- misaH
- Příspěvky: 13459
Re: Postup řešení integrace složitějšího součinu
↑ adamatematika:
kde je 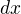 ?
?
Offline
#12 14. 11. 2018 13:15
- adamatematika
- Zelenáč

- Příspěvky: 7
- Škola: vut fast
- Reputace: 0
Re: Postup řešení integrace složitějšího součinu
↑ Aspro1:
dx jsem zapomel dopsat, ano tedy bude to absolutni hodnota z x?
MATEMATIKADAM
Offline
#13 14. 11. 2018 13:23
Re: Postup řešení integrace složitějšího součinu
↑ adamatematika: Ano. Musíme rozlišit případy, kdy  a kdy
a kdy  . Napsal jsi to zatím pro
. Napsal jsi to zatím pro  . Dej tam substituci
. Dej tam substituci 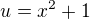 . Potom to vyřeš i pro
. Potom to vyřeš i pro  .
.
Offline
#14 14. 11. 2018 14:34 — Editoval adamatematika (14. 11. 2018 14:34)
- adamatematika
- Zelenáč

- Příspěvky: 7
- Škola: vut fast
- Reputace: 0
Re: Postup řešení integrace složitějšího součinu
 pro
pro 
MATEMATIKADAM
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Postup řešení integrace složitějšího součinu

 .
. . Vyřeš to i pro
. Vyřeš to i pro