Matematické Fórum

Kleanthés · 13. 11. 2018 21:06

Zdravím, chtěl bych vám ukázat své vysvětlení důkazu o spojitosti složené funkce v bodě. Jak se uvedená věta dokazuje jsem se díval, ale nejsem si jist, zdali všemu správně rozumím. Prosím tedy o kontrolu správnosti a vyjádření k srozumitelnosti důkazu.

Věta:
Budiž funkce y=g(x) spojitá v bodě a; dále budiž funkce f(y) spojitá v bodě g(a). Potom funkce f(g(x)) je spojitá v bodě a.

Důkaz:
Vyjdeme z předpokladu věty.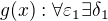

$g(x): \forall \varepsilon _{1} \exists \delta _{1}$ tak, že $|x-a| < \delta _{1}\Rightarrow |g(x)-g(a)|<\varepsilon _{1}$
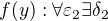$f(y): \forall \varepsilon _{2} \exists \delta _{2}$ tak, že $|y-g(a)| < \delta _{2}\Rightarrow |f(y)-f(g(a))|<\varepsilon _{2}$

Můžeme zvolit 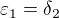$\varepsilon _{1}=\delta _{2}$ a dostáváme tak tvrzení ve tvaru

$(A \Rightarrow B) \wedge (B \Rightarrow C)$

Z toho ovšam plyne $A \Rightarrow C$ tedy $|x-a| < \delta _{1} \Rightarrow |f(g(x))-f(g(a))|<\varepsilon _{2}$

Tím je věta dokázána.

krakonoš · 13. 11. 2018 22:16

↑ Kleanthés:
Na prvni pohled chybu nevidim.Mohou se i jini vyjadrit.

Kleanthés · 14. 11. 2018 14:25

↑ krakonoš:
Já dosti zápolil s Jarníkovým důkazem, než jsem ho (snad) pochopil a přepsal jej právě do této podoby, která mi osobně připadá srozumitelnější. Vím, že matematici moc nepoužívají symbol pro implikaci, ale není mi jasné proč.

Tady je ten Jarníkův důkaz.
//forum.matweb.cz/upload3/img/2018-11/01840_IMG_0013.jpg

vlado_bb · 14. 11. 2018 14:39

Kleanthés napsal(a):
↑ krakonoš:
... matematici moc nepoužívají symbol pro implikaci, ale není mi jasné proč.

Pretoze vzajomne suvislosti formul su zrejme zo sprievodneho textu.

Kleanthés · 14. 11. 2018 16:26

↑ vlado_bb:
Proč psát nějaký text, když můžu použít jasný a stručný symbolický zápis? Proč používat místo symbolu implikace dvojtečku?

vlado_bb · 14. 11. 2018 16:33

↑ Kleanthés: Dvojbodku nepoužívam, ale súvislý text preto, lebo beriem ohľad na čitateľa. Mne osobne sa neporovnateľne lepšie číta normálny text, ako postupnosť formul bez sprievodných slov.

Bati · 14. 11. 2018 17:15

Ahoj ↑ Kleanthés:,
to, co jsi napsal je jen jakesi schema, jak se ta veta dokazuje, ale neda se to povazovat za dukaz. Mas 2 predpoklady: f je spojita a g je spojita. A ted resis ulohu, ze dostanes nejake epsilon>0 a musis rict jak k nemu zkonstruovat delta, aby |f(g(x))-f(g(x_0))|<epsilon pro vsechny x z delta okoli x.

Kleanthés · 14. 11. 2018 18:18

Bati · 14. 11. 2018 19:46

O to mi neslo. Zeptam se teda znovu: Rekneme, ze ti zadam epsilon=1. Jak zvolis delta? Z dukazu musi byt tohle jasne (nebo aspon to, ze takove delta existuje).

Kleanthés · 14. 11. 2018 20:52

↑ Bati:
Z důkazu by mělo vyplývat, že takové delta existuje (ano, jeho přesnou hodnotu neznáme). Víme totiž, že f(y) je spojitá v g(a), tedy existuje nějaké éta pro libovolné epsilon. Dále víme, že g(x) je spojitá v a, tedy pro libovolné éta existuje delta.

Matematické Fórum

#1 13. 11. 2018 21:06

Věta o spojitosti složené funkce - důkaz

#2 13. 11. 2018 22:16

Re: Věta o spojitosti složené funkce - důkaz

#3 14. 11. 2018 14:25

Re: Věta o spojitosti složené funkce - důkaz

#4 14. 11. 2018 14:39

Re: Věta o spojitosti složené funkce - důkaz

Kleanthés napsal(a):

#5 14. 11. 2018 16:26

Re: Věta o spojitosti složené funkce - důkaz

#6 14. 11. 2018 16:33

Re: Věta o spojitosti složené funkce - důkaz

#7 14. 11. 2018 17:15

Re: Věta o spojitosti složené funkce - důkaz

#8 14. 11. 2018 18:18

Re: Věta o spojitosti složené funkce - důkaz

#9 14. 11. 2018 19:46

Re: Věta o spojitosti složené funkce - důkaz

#10 14. 11. 2018 20:52

Re: Věta o spojitosti složené funkce - důkaz

Zápatí