Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#151 06. 11. 2018 01:54 — Editoval krakonoš (06. 11. 2018 10:24)
Re: Limitny maraton
↑↑ vanok:Ahoj.
Ano ,v tom s tebou souhlasim.Jen me zarazilo to zadani,ze nebylo uvedeno,aby se to zkoumalo v zavislosti na volbe prvniho clenu a ten byl zadan jako parametr.
Mozna u pripadu,kdy je u0 napr 100,by stacilo dokazat,ze posl klesa,je zdola omezena,takze ma limitu,kterou nalezneme jako reseni rovnice x rovno odmocnina (2x plus 3).
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#152 06. 11. 2018 02:20 — Editoval krakonoš (06. 11. 2018 02:24)
Re: Limitny maraton
↑↑ vanok:Ahoj.
Jeste k prikladu 40.
Reseni nabidla Marian.Ta si vsimla,ze castecny soucet rady lze zapsat jako rozdil dvou castecnych souctu harmonickych rad delky 2n a n.Spocteme limitu rozdilu castecneho souctu rady delky n a logaritmu n pro n jdouci do nekonecna .Tento rozdil bude Eulerova Mascher konstanta.Podobne u druhe rady.Odectenim obou limit dostaneme,ze log(2n)-log(n) je rovno nasi zadane rade. Aspon tak to vidim ja.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#153 06. 11. 2018 03:25
Re: Limitny maraton
↑ krakonoš:
Cau, to si chcela hovorit tu o priklade 42.
No, tu vlastne ked urobis poctivo cele cvicenie mas vseobecne riesenie. A to je krajsia praca ako riesit specialne pripady.
Mozno pridam este dalsie problemy o rekurentnych postupnostiach. To sa tu na fore zatial vela nevidelo.
No aj ked sme to nekreslili, na grafe funkcie f sa pekne vidi ako to funguje.
Dobru noc.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#154 06. 11. 2018 12:04
Re: Limitny maraton
Problem (43).
Vysetrite postupnost 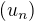 ak
ak 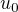 je dane a
je dane a 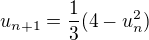
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#155 07. 11. 2018 16:42
Re: Limitny maraton
↑↑ Pavel:
Cau.
Vzhledem k tomu,ze prave probiha vyuka limit,rozhodla jsem se uvest i jine postupy jiz starych uloh.
Cviceni 5.
Upravime cleny ve velkych zavorkach,dostaneme pak uvnitr velkych zavorek cleny 1-x a 1plusx. Budeme pocitat limitu jdouci do nekonecna ,misto jdouci k nule,takze misto x dosadime 1/x a obracene. Vypocet se hodne zjednodusi. Misto k nule zprava pujdeme do plus nekonecna.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#156 07. 11. 2018 17:24
Re: Limitny maraton
↑↑ vytautas:
Co se tyce cviceni 2,
zde po vytknuti a naslednem vykraceni 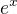 nebude uz ve jmenovateli neurcity vyraz,pocitame-li limitu citatele,pristoupime k vypoctu logaritmu citatele.Dale vyuzijeme upravy pomoci rozdilu ctvercu,podelime citatele i jmenovatele x.Ve jmenovateli rozdelime zlomek ve dva zlomky .Dale vyjadrime x jako odmocninu x nadruhou a dame pod jednu odmocninu.A dostaneme 1/2.Cili vysledek bude
nebude uz ve jmenovateli neurcity vyraz,pocitame-li limitu citatele,pristoupime k vypoctu logaritmu citatele.Dale vyuzijeme upravy pomoci rozdilu ctvercu,podelime citatele i jmenovatele x.Ve jmenovateli rozdelime zlomek ve dva zlomky .Dale vyjadrime x jako odmocninu x nadruhou a dame pod jednu odmocninu.A dostaneme 1/2.Cili vysledek bude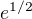 .
.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#157 07. 11. 2018 17:29
#158 07. 11. 2018 17:47
#159 07. 11. 2018 20:40 — Editoval vanok (08. 11. 2018 01:19)
Re: Limitny maraton
Ahoj ↑ krakonoš:,
Male myslienky.
Pokial, v cviceniach sa objavilo dobre a jasne riesenie, ktore je schopny najst ( alebo aspon rozumiet) student, tak je to je dostatocne uspokovive.
Co je aj pripad Cvicenia (2).
V tom cviceni je dobre pochopit, ze 1 v menovateli je « nepodstatna » .... a k tomu sa dopracoval po usmerneni kolega vytaukas. Preto som tam nedal ziadne ine riesenie.
Niekedy je tiez rychle pouzit « mocne » teoremy. Ale pouzitie, zdanlivo komplikovanych postupov bez nich, tiez moze viest k rieseniu. ( a po porovnani postupov, niekedy sa da vidiet, ze druhy postup obsahuje myslienky dokazu mocnej teoremy...)
Co je dolezite, podla mna, je schopnost riesit cvicenia a na to je pre normalnych ludi jedina metoda, pokusat sa riesit samostatne co najviac cviceni. ( mysli na zname prislovie :
L'appétit vient en mangeant).
A ozaj problem (43) je trochu komplexnejsi ako predosly. Zacala si ho « vysetrovat »?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#160 07. 11. 2018 23:47
Re: Limitny maraton
↑ vanok:Co se tyce cviceni (43),pomoci Bolzano Cauchyho podminky lze dokazat,ze posloupnost konverguje pro u0 
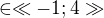 . Pro hodnotu parametru 4 je limita -4, jinak 1.Tak to vidim ja. Mohou i jini lide uvest sve postupy.
. Pro hodnotu parametru 4 je limita -4, jinak 1.Tak to vidim ja. Mohou i jini lide uvest sve postupy.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#161 08. 11. 2018 02:00 — Editoval vanok (13. 11. 2018 08:40)
Re: Limitny maraton
Ahoj ↑ krakonoš:,
Problem (43).
Pokracuj vo vysetrovani. ( pouzitie grafu nie je riesenie ale moze pomoct), zatial si nedala ani presnu presnu odpoved a ani si nic nedokazala.
To mas pravdu, aj ini mozu reagovat.
Pre tych co chcu napredovat davam hint a otazky, ktore mozu pomoct.
Ake su mozne hodnoty pre pripadnu hodnotu limity  .
.
Pre ake 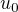 dana postupnost diverguje k
dana postupnost diverguje k  .
.
Pre ake 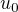 dana postupnost je rastuca (a omedzena?).
dana postupnost je rastuca (a omedzena?).
Pre ake 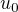 dana postupnost je konstantna?
dana postupnost je konstantna?
Pre ake 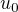 dana postupnost sa stane stacionarna?
dana postupnost sa stane stacionarna?
( vsetko je potrebne dokazat).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#162 08. 11. 2018 08:39 — Editoval krakonoš (08. 11. 2018 08:58)
Re: Limitny maraton
↑ vanok:
Pro ktera u0 pisloupnost konverguje,urcuje jednoznacne BolzanovoCauchyho kriterium.To je dukaz.Tato metoda je vseobecne uznavana a je popsana v kazde ucebnici analyzy,i v Jarnikovi.Zadnou grafiku jsem nepouzila.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#163 08. 11. 2018 10:12 — Editoval vanok (08. 11. 2018 10:41)
Re: Limitny maraton
Cau ↑ krakonoš:,
Tak pockaj na uplny dokaz, za urcity cas ho sem dam.
Inac co sa stane v pripade ak napr. 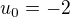 ? ( o ktorom nic nepises)
? ( o ktorom nic nepises)
Male poznamky.
Vysetrit postupnost znamena, ze potom citatel jeho “vysetrenia” bude vediet potom ako sa sprava ta postupnost pre kazde 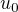 .
.
Citat nejaku knihu, aj od na genialnejsieho autora nestaci na to, ze jeho citatelia budu vediet vsetko riesit bez prace a podrobneho vysvetlenia.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#164 08. 11. 2018 10:31
#165 11. 11. 2018 23:38 — Editoval vanok (13. 11. 2018 08:37)
Re: Limitny maraton
Problem (43) riesenie.
Uz vyssie som napisal, co znamena vyraz vysetrit. ( to nie je hadanie a napisanie nejakej nepresnej odpovedi ... aspon ak hladate mat vyborne hodnotenie od vasho skusajuceho )
Tiez, som napisem, co iste kazdy skusajuci by chcel vidiet od poctiveho studenta. ( Pozor, nejake jednoduche uvahy necham doplnit citatelovy).
Najprv je jasne, ze mozne hodnoty pre pripadnu hodnotu limity  splnuju
splnuju  co je ekvivalentne (overte ) z
co je ekvivalentne (overte ) z  alebo
alebo  .
.
Tiez lahko ukazeme, ze 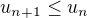 len a len ak
len a len ak ![kopírovat do textarea $ u_n \in [-4;1]$](/mathtex/8c/8c83e7c8825e1bf037c16cd4bc736251.gif) .
.
I) Ak  dana postupnost diverguje k
dana postupnost diverguje k  .
.
Mat. indukciou ukazeme ze dana postupnost je klesajuca a ze nie je dolno ohranicena, ak by bola tak tak by bola konvergentna a jej limita  co je nemozne. Tak je divergentna.
co je nemozne. Tak je divergentna.
II) Ak  , tak
, tak  a mozme s inspirovat uvahou v I)
a mozme s inspirovat uvahou v I)
III) ![kopírovat do textarea $u_0 \in ]-4;0]$](/mathtex/07/075dc3dbf380a719e856dbdf8305db4b.gif) ; funkcia
; funkcia 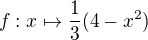 je rastuca na
je rastuca na ![kopírovat do textarea $[-4 ;1]$](/mathtex/7f/7ff677a18657c0b947e399e3397224e4.gif) vtedy prve cleny postupnosti su rastuce no vsak
vtedy prve cleny postupnosti su rastuce no vsak  nemoze byt jeho majorant (tak nie je mozne, ze jeho limita je v
nemoze byt jeho majorant (tak nie je mozne, ze jeho limita je v ![kopírovat do textarea $]-4;0]$](/mathtex/d9/d9a782d007a2d0a0d99c25ae95f42847.gif) ) a preto existuje prirodzene
) a preto existuje prirodzene 
take, ze  a
a 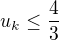 ( lebo
( lebo  je maximum funkcie
je maximum funkcie  )
)
To doriesime v V).
IV) Ak 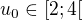 , tak
, tak ![kopírovat do textarea $u_1 \in ]-4;0]$](/mathtex/b7/b7354fd8327b4100b988606ea43a46ce.gif) a sme v situacii III) ( vdaka zmene indexov).
a sme v situacii III) ( vdaka zmene indexov).
V) Pre ![kopírovat do textarea $u_0 \in [0;2]$](/mathtex/7f/7fb2f988ad8691e6e36bf33537273404.gif) vsetko cleny postupnosti su v intervale vzdy
vsetko cleny postupnosti su v intervale vzdy ![kopírovat do textarea $[0;2]$](/mathtex/06/064c9662b565be74e19f087835d479aa.gif) .
.
Funkcia  je na nom klesajuca, a preto postupnost
je na nom klesajuca, a preto postupnost 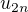 je rastuca pre
je rastuca pre ![kopírovat do textarea $u_0 \in [0;1]$](/mathtex/28/28c97221203edf2f5539d48a561d17ec.gif) (lebo ak
(lebo ak  tak
tak  )
)
Mozne limity pre tuto postupnost splnuju 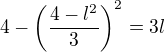 co da
co da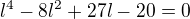 a este
a este 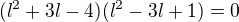 ; realne korene poslednej rovnice su
; realne korene poslednej rovnice su  a
a  . A tu vyhovuje len
. A tu vyhovuje len  .
.
A tak tu tato rastuca postupnost ma majorant  a jej limita je
a jej limita je  .
.
Postupnost 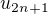 ma tu istu limitu.
ma tu istu limitu.
Cize postupnost  konverguje v tomto pripade k
konverguje v tomto pripade k  .
.
VI) Na viac:
Pre  dana postupnost je konstantna
dana postupnost je konstantna 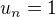 .
.
Pre 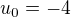 dana postupnost je tiez konstantna.
dana postupnost je tiez konstantna.
Pre  dana postupnost je stacionarna od
dana postupnost je stacionarna od 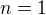 .
.
Zhrnutie.
Pre  postupnost diverguje (k
postupnost diverguje (k  ),
),
pre  postupnost konverguje k
postupnost konverguje k  .
.
A pre 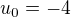 dana postupnost je konstantna
dana postupnost je konstantna 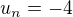 .
.
Pre  dana postupnost je stacionarna od
dana postupnost je stacionarna od 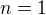 .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#166 14. 11. 2018 18:04
Re: Limitny maraton
Problem (44).
Nech je dana postupnost 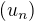 taka, ze
taka, ze

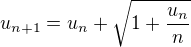 , n nenulove prirodzene cislo .
, n nenulove prirodzene cislo .
Dokazte, ze postupnost  konverguje.
konverguje.
Vieme nast jej linitu?
Poznamka. Problem z webu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#167 15. 11. 2018 02:00
Re: Limitny maraton
↑ vanok:
Ahoj, ja bych rekl, ze kdyz  , potom
, potom  pro velka
pro velka  . Kdyz to dosadim do rovnice, potom ziskam
. Kdyz to dosadim do rovnice, potom ziskam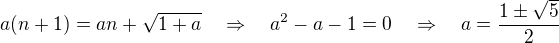 .
.
Protoze jsou evidentne vsechna  kladna, je
kladna, je 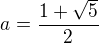 .
.
Zlaty rez je tedy jedina mozna limita 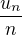 . Zbyva ukazat, ze tomu tak doopravdy je:
. Zbyva ukazat, ze tomu tak doopravdy je:
Offline
#168 15. 11. 2018 04:03 — Editoval vanok (15. 11. 2018 08:54)
Re: Limitny maraton
Servus ↑ laszky:,
Dakujem, ze ta moje problemy zaujimaju.
Skutocne si ukazal, ze mozna limita je a ( zlaty rez). ( cize 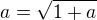 ). Co si potom dokazal.
). Co si potom dokazal.
Druhy dokaz.
No vsak, zda sa mi, ze tento dokaz je jednoduchsi.
Polozim, 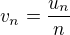 .
.
Mame, ak  ,tak aj
,tak aj  .
.
Tiez mame rekurentnu relaciu : 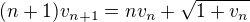 .
.
Indukciou ukazeme, ze  je dolna hranica pre
je dolna hranica pre 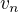 .
.
Preto aj  , co da, ze postupnost
, co da, ze postupnost 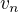 je klesajuca....a tak konverguje ....oznacme jej limitu
je klesajuca....a tak konverguje ....oznacme jej limitu  .
.
A  .
.
Akoze  , konverguje ku
, konverguje ku  ,
,
a  musi byt
musi byt  inac mame spor (
inac mame spor (  by divergovala ).
by divergovala ).
Co da 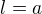 .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#169 15. 11. 2018 15:27 — Editoval krakonoš (15. 11. 2018 15:53)
Re: Limitny maraton
↑ laszky:Ahoj.
Nad timto problemem jsem premyslela take.Posloupnost un ma kladne cleny a je rostouci,kdyby byla shora omezena,mela by mit konecnou limitu . Rozdil clenu u( n plus 1)- u(n) ale jde k nule,zatimco vyraz pod odmocninou jde k 1.Z toho usuzuji ,ze un neni omezena shora.
Co kdyby vsak un mela limitu nekonecno?To by tez vyhovovalo rovnici jako a.A jak vyvratit,ze neni radove vic jak n,to by limita podilu un/n sla do nekonecna.Jedine to asi zkusit pro to vase a konecne,a tim to cele vyvratit,protoze nemuze mit dve ruzne limity.
Diky.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#170 17. 11. 2018 16:16
Re: Limitny maraton
Problem (44).
Ahoj ↑ krakonoš:,
Zaujimat sa o postupnost  je iste zabavne, ale pozor tu nam ide o
je iste zabavne, ale pozor tu nam ide o 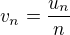 .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#171 17. 11. 2018 18:47
Re: Limitny maraton
↑ vanok:
Ahoj.
Ja totiz myslela,ze kdyz limita un existuje a je nekonecno ( viz vyse) a ze zadani je patrne,ze u(n) je radu n.Tak to dokazuje i existenci a konvergenci limity u(n)/n.A zlaty rez(t.j.a) musi byt limitou u(n)/n.,protoze jediny vyhovuje rovnici ,kde figuruje u(n)/n pak by se uz asi nemuselo dokazovat,ze u(n)/n jde v absolutni hodnote k nule???
Lida
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#172 18. 11. 2018 00:34
Re: Limitny maraton
↑ krakonoš:, prestuduj si .↑ vanok:
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#173 19. 11. 2018 16:22 — Editoval krakonoš (19. 11. 2018 16:32)
Re: Limitny maraton
↑ vanok:
Ahoj.
Prostudovala jsem si peclive tvuj dukaz.To,ze je posloupnost v(n) konvergentni,uz vyplyva Jen z toho,ze je klesajici a zdola omezena,protoze neni zaporna.Takze musi mit limitu a,tam vyhovuje ta rovnice popsana vyse.
Lida
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#174 24. 11. 2018 13:34 — Editoval vanok (24. 11. 2018 13:35)
Re: Limitny maraton
Problem (45)
Vysetrite 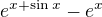 v okoli
v okoli  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#175 26. 11. 2018 20:42
Re: Limitny maraton
Problem(45)
Hint. Ukazte, ze limita v  nexistuje.
nexistuje.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

 a
a 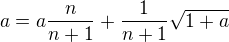 ziskame
ziskame