Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#51 14. 11. 2018 18:08
Re: Různé napětí - stejný proud?
↑↑ KennyMcCormick:
Co na to mám říct? Možná se někdy v historii takovýto přístup používal, ale podle mě je to nesmysl.
Cituji:
Skutečnost, že uvnitř článku je E=0 lze považovat za výsledek složení dvou elektrických polí, a to pole o intenzitě Est, které je vyvoláno náboji těles A, B (to jsou póly zdroje) a pole o intenzitě Ei, které není elektrostatického původu. Platí tedy E = Est + Ei = 0.
To je sice super, a já i do jisté míry chápu, odkud to pochází (popíši později), ale žádné elektrické pole E neelektrického původu prostě neexistuje, takže takže to celé nedává smysl.
Intenzita elektrického pole E je definována tím, že je to síla působící na malý testovací náboj (můj náboj, který já si zvolím a použiji jako testovací či měřící přístroj). A zdrojem elektrického pole je jen elektrický náboj (nebo změna B), nic jiného pole E nemůže vytvořit.
Ale odkud to všechno pochází - v elektrochemii existuje pojem zvaný "elektrochemický potenciál". Jde o to, že částice roztoku (iont, nebo třeba i samotný elektron) může být "poháněn" jak elektrickým polem, tak koncentračním gradientem. A obě působení se chovají do jisté míry stejně, nelze je od sebe oddělit. Běžně k tomu dochází třeba na buněčných membránách různých buněčných organel. Na nabité částice působí jak osmotický tlak, tak elektrické pole. A jejich účinky se sčítají (pro konkrétní typ částice - to je dost podstatná věc, na jinou částici může osmotický tlak působit jinak, závisí na koncentraci těch částic, zatímco elektrická síla závisí jen na náboji).
Takže pokud bychom nemluvili o elektrickém potenciálu, ale o elektrochemickém, zavedli si nějakou intenzitu elektrochemického pole ECH, a udělali z ní integrál po uzavřené křivce, tak by zřejmě vyšel roven tomu napětí naprázdno, či elektrochemickému napětí. Já ale nevím, jestli to lze udělat takto jednoduše, protože eletkrochemický potenciál je obecně jiný pro každou částici, a nevím, jestli jej lze nějak definovat i uvnitř kovu nebo v izolantu. Je to věc, která se týká chemických roztoků.
Dělat z toho nějakou "intenzitu el. pole neelektrického původu" je podle mě nesmysl. Elektrické pole musí působit na částice jen podle jejich náboje. Nicméně to (ten elektrochemický potenciál, a z něj plynoucí představa elektrochemické intenzity silového pole) dává celkem smysl - ale jen pro elektrochemické zdroje.
PS: co jsem napsal o elektrochemii není určitě zcela správně. Za napětí chemického článku asi nemůže koncentrační gradient, nýbrž to, co nazval Nernst jako "rozpouštěcí tlak"...já nevím, jestli je to úplně to samé, nebo něco úplně jiného, nebo se to do jisté míry podobá...
Já to vidím asi tak, že na nabité částice v roztoku působí ten chemický potenciál - ten přesouvá náboje z jedné elektrody na druhou - a proti tomu působé elektrický potenciál, který náboje, jež už byly přesunuty, vytváří. Až se ty potenciály vyrovnají, tak už se žádné další náboje nepřesouvají. V tom ustáleném stavu je tedy rozdíl elektrických potenciálů to, co nazýváme napětí naprázdno, a rozdíl chemických potenciálů tím elektromotorickým napětím (i když by zde byl mnohem lepší výraz "chemické napětí").
No a pak nastoupí ta abstraktní představa, že když náboje mezi elektrodami bude přenášet něco jiné, než rozdíl chemických potenciálů, budeme to nazývat také elektromotorické napětí. Jenže se nějak nedomyslelo, že existují i jiné varianty než ustálený rovnovážný stav statistické mechaniky (to je ta chemie), a že v proměnném el. mag. poli platí trochu složitější zákony a elektrický potenciál tam vůbec nelze zavést.
Offline
#52 15. 11. 2018 02:49
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
Já bych tedy řek, že z toho nafoceného textu plyne, že EMN je na výstupu zdroje, pokud je úbytek napětí na vnitřním odporu 0. Když ho zatížím, je tam napětí menší.
Myslel jsem ideální zdroj (bez vnitřního odporu) v obvodu, nebo jakýkoliv otevřený zdroj.
Máš pravdu, že zdroj s vnitřním odporem připojený do obvodu bude mít jiné svorkové napětí.
↑ MichalAld:
Co na to mám říct?
Tím jsem myslel, jestli to považuješ za správné/chybné. 🙂
elektrické pole E neelektrického původu prostě neexistuje
Oni píšou elektrické pole neelektrostatického původu, což chápu jako elektrické pole nevyvolané stojícími náboji.
(Ještě může být vyvolané pohybujícími se el. náboji, nebo proměnným mag. polem.)
Takže pokud bychom nemluvili o elektrickém potenciálu, ale o elektrochemickém, zavedli si nějakou intenzitu elektrochemického pole ECH, a udělali z ní integrál po uzavřené křivce, tak by zřejmě vyšel roven tomu napětí naprázdno, či elektrochemickému napětí.
Tak jsem to pochopil taky.
Buď zahrnu do  i elektromotorické síly, a celkové
i elektromotorické síly, a celkové  bude nula, čímž vysvětlím, že je to ustálený stav.
bude nula, čímž vysvětlím, že je to ustálený stav.
Nebo je tam nezahrnu, a v tom případě  nebude nula.
nebude nula.
Je to otázka názvosloví, jestli elektromotorické síly sečtu s elektrostatickými silami, nebo ne, tudíž je to rozdíl v sémantice, a ne ve fyzice. Je to tak?
(V tom případě by to, zda definice EMN přes práci je ekvivalentní definici  , byla také otázka názvosloví.)
, byla také otázka názvosloví.)
a že v proměnném el. mag. poli platí trochu složitější zákony a elektrický potenciál tam vůbec nelze zavést
Jak to vypadá v případě stejnosměrných zdrojů, které obsahují střídavý proud?
U stejnosměrných zdrojů je mi to jasné - elektrostatická síla je konzervativní, takže pokud chci vytvořit stálé napětí, musí být kompletně udržováno neelektrostatickými silami. Tudíž napětí vyvolané neelektrostatickými silami musí být přesně rovno (u ideálního zdroje) napětí na svorkách zdroje kvůli zákonu zachování energie.
Platí stejný princip (přes zákon zachování energie) i u stejnosměrných zdrojů obsahujících střídavý proud? (Jako je obvod na obrázku?) Zdá se mi, že by měl(?)
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#53 15. 11. 2018 17:03 — Editoval MichalAld (15. 11. 2018 17:03)
Re: Různé napětí - stejný proud?
Mám několik dost pádných důvodů, proč by se takovýto přístup používat neměl.
1) Představa "pole neelektrostatického původu" nebo obecně jakéhokoliv původu je úplně proti představě pole samotného. Myšlenka pole je taková, že když už jej známe, nemusíme se starat o to, jakého je "původu", čím bylo vytvořené. Pokud známe rozložení intenzity E a B v prostoru a čase, je to vše, co potřebujeme znát. Výsledek experimentu nemůže záviset na tom, jakého je pole původu, čím bylo vytvořeno. Ne - závisí jen na vlastnostech toho pole.
Dokonce je snaha, aby experimen závisel na vlastnostech pole LOKÁLNĚ. Tj síla, která působí na nabitou částici v nějakém místě je určena jen vlastnostmi pole v tom místě. Tohle se však né vždy daří - v kvantové mechanice je znám experiment, kdy pole (alespoň tedy pole E a B) působí na částici nelokálně. Ale to už s tímhle nesouvisí.
2) Dále - k té představě "pole neelektrostatického původu" - elektrostatické pole existuje jen v učebnicích. Ve skutečném světě nic takového neexistuje. Veškeré pole pochází od nabitých částic tohoto světa (elektronů, protonů a možná i dalších) a tyhle částice se trvale pohybují.
A jak už jsem zmínil, můžeme definovat elektrostatické pole (takové, že dE/dt = 0), ale nemůžeme požadovat jeho "původ", pole si nepamatuje svůj původ. Musíme si vystačit s tím, co je teď.
Ale ten nejzákladnější problém - nemůžeme si s fyzikálními veličinami dělat takovéto psí kousky. Do veličiny E nemůžeme zahrnout něco jen proto, že se nám to zrovna hodí. Veličina E je zcela přesně definována, jako síla působící na velmi malý zkušební náboj (a přepočtená na jednotkový náboj). Veličina E musí splňovat Maxwellovy rovnice a potažmo tedy také třeba Lorentzovskou invarianci. Nemůžeme si k ní přidat jinou veličinu jen proto, že je zrovna taky konzervativní. To je podle mě úplně špatně - a určitě to nepomůže žádnému pochopení problému.
Navíc - my nevíme, jestli se ta neelektrická síla chová stejně jako elektrická. To bych mohl za chvíli říkat, že část elektrického pole pochází od pole vytvořeného náboji a část pochází od gravitačního pole. Speciálně jsem kvůli tomu vymyslel i "gravitační baterii" abych to mohl demonstrovat - možná to sem později napíši.
Z toho, že můžu sčítat síly působící na částici neplyne, že můžu bez problému sečíst i ta silová pole. Já si třeba myslím, že ta chemická část síly, co působí na částici, nezávisí nijak zvlášť na jejím náboji, zatímco elektrická složka síly ano. Takže když použiji dvě různé testovací čátice, jednu s nábojem e- a druhou s nábojem 2e-, dostanu pokaždé jinou hodnotu takovéto intenzity - což je úplně špatně, protože intenzita by neměla na testovací částici záviset.
Všechno je to prostě narafičené jen na jednu konkrétní situaci a nemá to obecnou platnost. A navíc to celou situaci jen zamlžuje, namísto aby ji to osvětlovalo.
Offline
#54 15. 11. 2018 17:16 — Editoval MichalAld (15. 11. 2018 17:20)
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
Oni píšou elektrické pole neelektrostatického původu, což chápu jako elektrické pole nevyvolané stojícími náboji.
Já ten pojem odmítám používat, protože je nesmyslný.
Jak se pozná, že náboje "stojí" ? Máme teorii relativity, akumulátor musí fungovat i když jej povezu v autě...
A pokud tím chtěl básník říci, že příčinou vzniku napětí v baterii je pohyb těch částic (že ta neelektrostatická složka E, co nám vlastně tvoří EMN, je způsobená pohybem částic v roztoku) tak je to taky špatně.
Offline
#55 16. 11. 2018 04:26
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
Ale ten nejzákladnější problém - nemůžeme si s fyzikálními veličinami dělat takovéto psí kousky. Do veličiny E nemůžeme zahrnout něco jen proto, že se nám to zrovna hodí.
Původně jsem si myslel, že tahle intenzita je něco, co bych měl možnost - alespoň v principu - připočíst k elektrostatické intenzitě (a získat nulu), protože ve zdroji (v galvanickém článku) netečou v odpojeném stavu žádné proudy (nebo každý proud, který teče, je vykompenzovaný opačným proudem).
Ale to by zase protiřečilo Maxwellovým rovnicím, takže to asi není pedagogicky vhodné...
(Minimálně část toho pole  by měla být elektrická (protože chemické reakce jsou poháněny elektrickými interakcemi), ale chemické reakce (asi) částečně vyžadují i síly, které nejsou elektrické, a hlavně nejsou vysvětlitelné klasickým elektromagnetismem)
by měla být elektrická (protože chemické reakce jsou poháněny elektrickými interakcemi), ale chemické reakce (asi) částečně vyžadují i síly, které nejsou elektrické, a hlavně nejsou vysvětlitelné klasickým elektromagnetismem)
Tohle se však né vždy daří - v kvantové mechanice je znám experiment, kdy pole (alespoň tedy pole E a B) působí na částici nelokálně.
Myslel jsem, že i v kvantové mechanice je všechno přesně lokální (jinak by byla narušena kauzalita), ale se zakládáním nového vlákna na tohle téma budu muset počkat na příští rok, až se začnu učit kvantovou mechaniku...
Z toho, že můžu sčítat síly působící na částici neplyne, že můžu bez problému sečíst i ta silová pole. Já si třeba myslím, že ta chemická část síly, co působí na částici, nezávisí nijak zvlášť na jejím náboji, zatímco elektrická složka síly ano. Takže když použiji dvě různé testovací čátice, jednu s nábojem e- a druhou s nábojem 2e-, dostanu pokaždé jinou hodnotu takovéto intenzity - což je úplně špatně, protože intenzita by neměla na testovací částici záviset.
To by mělo být ultimátně vykompenzované něčím jiným, protože v ustáleném stavu tam žádný celkový proud neteče, takže by to (v nějakém smyslu) mělo být ekvivalentní situaci, kdy (na dostatečně velkém měřítku) je intenzita nula. Ale ve skutečnosti to tak stejně není, takže to asi nemá cenu hlouběji rozebírat.
↑ MichalAld:
Jak se pozná, že náboje "stojí" ? Máme teorii relativity, akumulátor musí fungovat i když jej povezu v autě...
Oni to mysleli takhle: Představ si elektrický obvod, ve kterém se pokusíme napětí udržet pouze pomocí dvou stojících nábojů - kladného a záporného (připojených k obvodu v místě, kde obvykle stává zdroj).
Tyto stojící náboje působí na volné elektrony v obvodu kovu elektrostatickou silou a v důsledku toho všechny elektrony v obvodu rychle zaujmou rovnovážnou pozici a proud už protékat nebude.
Proto v každém zdroji musí být napětí udržováno silami, které nejsou elektrostatické.
Autoři to vysvětlili na příkladu se dvěma stojícími náboji, takže bych interpretoval "elektrostatická síla" = "síla způsobená stojícím elektrickým nábojem".
Speciální teorie relativity na tom tím pádem nic nemění.
Ale můžu svojí otázku přefrázovat, tak, že:
elektrické := elekrostatické
a
elektromotorické := neelektrostatické
V tom případě bych se ptal:
Jak to vypadá v případě stejnosměrných zdrojů, které obsahují střídavý proud?
U stejnosměrných zdrojů je mi to jasné - elektrická síla je konzervativní (pokud se nemění magnetické pole), takže pokud chci vytvořit stálé napětí, musí být kompletně udržováno neelektrickými (elektromotorickými) silami. Tudíž napětí vyvolané elektromotorickými silami musí být přesně rovno (u ideálního zdroje) napětí na svorkách zdroje kvůli zákonu zachování energie.
Platí stejný princip (přes zákon zachování energie) i u stejnosměrných zdrojů obsahujících střídavý proud? (Jako je obvod na obrázku?) Zdá se mi, že by měl(?)
Přemýšlel jsem, jestli proměnné magnetické pole v takovém zdroji nezpůsobí, že nemůžu tentýž argument použít, ale nakonec jsem došel k závěru, že ne - protože potřebuju jenom konzervativnost  podél obvodu, abych řekl, že rozdíl potenciálů v místě zdroje je možné udržet pouze neelektrickými (elektromotorickými) silami.
podél obvodu, abych řekl, že rozdíl potenciálů v místě zdroje je možné udržet pouze neelektrickými (elektromotorickými) silami.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#56 16. 11. 2018 09:14
Re: Různé napětí - stejný proud?
Tak jsem to konečně pochopil...důkazem toho, že celá ta argumentace v uvedené knížce je extrémně zavádějící je i to, že to popoletlo i mě...jak by řekl Hujer "I já jsem s tím měl problém". Je to nakonec docela jednoduché:
Pokud si důsledně představíme, že ve zdroji (třeba tom chemickém) působí na nabité částice krom elektrického pole E ještě i nějaké jiné pole, označme jej třeba D (a nebudeme jej v žádném případě považovat za nějakou část E), musíme se prostě ptát, jaké má to pole D vlastnosti, dříve, než s ním začneme počítat.
První, co nás napadne (zejména když člověk čte takový nápad, že D je taková část E) že by tedy mohlo mít obdobné vlastnosti jako E, jen bude mířit opačným směrem. Tedy že by to mohlo být konzervativní pole, nejlépe potenciálové pole (když o něm mluvíme jako o potenciálu, či napětí). Takže by mělo platit, stejně jako v elektrostatice, že
rot D = 0,
div D = něco.
Potom můžeme tedy i pole D vyjádřit jako gradient nějakého chemického potenciálu.
To je ale úplně špatně !!!
Kdyby to tak bylo, potom by integrál po (libovolné) uzavřené křivce musel být nulový (když rot D = 0). A zdroj by žádné napětí nedával, protože když rot E = 0 i rod D = 0, tak i rot (E+D) = 0.
Plyne z toho jediný závěr - v každém případě potřebujeme, aby rod D nulové nebylo. Potřebujeme pole D, které NENÍ KONZERVATIVNÍ. Ono to taky nakonec dává smysl, žejo, když z toho máme brát energii, nemůže to být konzervativní. Potom tedy nemůžeme mluvit o žádném potenciálu - kde je nenulová rotace pole, nelze potenciál zavést.
Pak už je to snadné - integrál z tohoto pole D po uzavřené smyčce vyjde nějaké číslo, a to je přesně to, čemu říkáme elektromotorické napětí.
Na první pohled je vidět, že pro indukované napětí (napětí indukované změnou magnetického toku) dostáváme to, na co jsme zvyklí.
Takže máme konečně univerzální definici, na které můžeme stavět. Já samozřejmě nevím, jak přesně to je, pokud je D proměnné v čase. Ale pokud je statické (dD/dt = 0), je to celkem snadné, a můžeme klidně vypočítat elektromotorické napětí i nějakého složitého zdroje. Jen si musíme dát pozor, že integrál závisí na zvolené uzavřené křivce - obecně je pro každou křivku jiný.
A teď se konečně dostáváme k tomu nejzajímavějšímu - jak toto pole D v chemickém článku vlatně vypadá.
PS: z výše uvedené argumentace na první pohled plyne, že "gravitační článek" co jsem zmińoval v předchozím příspěvku, by nemohl fungovat. Gravitační pole je konzervativní, má nulovou rotaci.
Offline
#57 16. 11. 2018 10:57
Re: Různé napětí - stejný proud?
Myslím, že ten obrázek 3.8 je prostě blbě a tudíž je blbě i celý text co se na něj odkazuje. Reálně máme sériově zapojené dva poločlánky a mezi nimi je elektrolyt. V nezatíženém stavu v elektrolytu není E, ani žádná protichůdná pole. Podmínky v něm jsou stejné, jako kdyby tam elektrody nebyly.
Samozřejmě se mohu mýlit, ale tuto chybu bych byl ochoten uznat jedině tehdy, kdyby za objev toho záhadného "protipole" (já bych ho značil M, abychom z E a M dostali EM napětí) autor knihy dostal nobelovku (spolu s teoretikem, který by k tomu odvodil polní částice) po té, co by v Cernu našli ty částice. :-)
Offline
#58 16. 11. 2018 14:33
Re: Různé napětí - stejný proud?
↑ edison:
Ten fyzik se jmenoval Walther Hermann Nernst, nobelovku dostal 1920, hi.
Také viz Nernstova rovnice
Offline
#60 16. 11. 2018 15:06 — Editoval edison (16. 11. 2018 15:07)
Re: Různé napětí - stejný proud?
Nernstova rovnice v sobě má běžné E, jen 2x a v sérii, takže tam je vše v pořádku. V opačném případě by měl problém prof. Kulhánek, že by ten jeho oblíbený obrázek s kostičkami obsahujícími jednotlivé částice mělo ještě jednu navíc, co by vyčnívala:-)
Autor knížky (nebo ten od koho obrázek převzal), ovšem udělal to záhadné antiparalelní pole situované do elektrolytu, čímž se dostal do rozporu s Nernstem i Maxwellem.
Offline
#61 16. 11. 2018 17:55
Re: Různé napětí - stejný proud?
Pole v elektrolytu je samozřejmě nesmysl, pole je jen ve velmi tenké vrstvě na povrchu elektrod.
Jinak to pole co z něj plyne elektromotorické napětí je pole pocházející ze statistické mechaniky. Není to zas až tak moc fundamentální fyzikální pole. Je to podobné, jako třeba teplotní pole - a gradient teploty nám také dokáže pohánět přenos tepla - a dokonce tak dokáže i vytvářet elektřinu, na termočlánku - a také na to nepotřebuješ žádné speciální částice.
Podobně je to s koncentračním polem - gradient koncentrace nám také dokáže pohánět částice.
Všechna tahle "statisticko-mechanická pole" mají svoji fundamentální příčinu, nejsou sama o sobě fundametání fyzikou. Akorát že to nedokážeme matematicky zvládnout (spočítat tepelný pohyb miliard částic) - takže nám nezbude než zavést pár dodatečných axiomů ohledně statistických vlastností těch částic a brát to jako fundamentální fyziku, i když víme, že ve skutenosti to tak úplně není.
Offline
#62 17. 11. 2018 04:48 — Editoval KennyMcCormick (17. 11. 2018 04:51)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
Potřebujeme pole D, které NENÍ KONZERVATIVNÍ.
Ano, správně. 🙂
Btw, našel jsem tady jednu z dalších rovnic (ale ne o chemickém článku), ve které se pole EM sil připočítává přímo k elektrické intenzitě, takže se to asi někdy dělá a někdy nedělá.
Taky jsem našel obecnou definici EM napětí:![kopírovat do textarea $\mathcal{E}=\oint[\textbf{E}+\textbf{v}\times\textbf{B}]\d\textbf{l}+\frac1 q\oint(\text{efektivní chemické síly})\d\textbf{l}+\frac1 q\oint(\text{efektivní termální síly})\d\textbf{l}$](/mathtex/cb/cb34e1330809a3e2e77d50e96993283f.gif)
Přemýšlel jsem nad tím, proč je indukovaná část EMN rovna ![kopírovat do textarea $\oint[\textbf{E}+\textbf{v}\times\textbf{B}]\d\textbf{l}$](/mathtex/61/61e6ce97eba6921c9b1638c94a82091b.gif) , a ne
, a ne  , a došel jsem k závěru, že je to kvůli případům, kdy vektor rychlosti není rovnoběžný/protiběžný s
, a došel jsem k závěru, že je to kvůli případům, kdy vektor rychlosti není rovnoběžný/protiběžný s 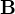 .
.
Zdá se mi, že tahle obecná definice EMN je ekvivalentní té definici přes práci. Je to tak?
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#63 17. 11. 2018 10:49
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
Btw, našel jsem tady jednu z dalších rovnic (ale ne o chemickém článku), ve které se pole EM sil připočítává přímo k elektrické intenzitě, takže se to asi někdy dělá a někdy nedělá.
Ono když už tomu člověk rozumí, a je si vědom omezení, jaké takové úvahy mají, tak to sečíst může. Ale obecně je to nesmysl.
Například intenzita elektrického pole E působí nějakým způsobem i na pohybující se permanentní magnet (pokud je pole homogenní, tak jen momentem, pokud je nehomogenní, tak možná i silou). A jsem si téměř jistý, že pole koncentračního gradientu nechá pohybující se permanentní magnet zcela chladným...
Prostě je třeba mít na paměti, že intenzita el. pole E není samostatná veličina, je to jen složka tenzoru elektromagnetického pole, a podle toho s ní také musíme zacházet. Zatímco pole koncentračního gradientu je skalární pole (správně tedy pole získané gradientem skalárního pole) a tím je plně určeno.
Takže sčítat to můžeme jen tehdy, když B = 0, což je právě ta situace, kterou nazýváme elektrostatika. Prostě když zapomeneme, že náboje v pohybu, nebo i jen soustava v pohybu nám vytvoří i magnetické pole.
Takže já bych to moc nesčítal. Aspoň pokud nám jde o fyzikální podstatu.
Offline
#64 17. 11. 2018 10:54
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
Taky jsem našel obecnou definici EM napětí:
Přemýšlel jsem nad tím, proč je indukovaná část EMN rovna, a ne
, a došel jsem k závěru, že je to kvůli případům, kdy vektor rychlosti není rovnoběžný/protiběžný s
.
Jo, to je dobrá definice. Ten člen v x B je tam pro situace, kdy se nám ta smyčka, podél které počítáme integrál, pohybuje. Je to sice z matematického hlediska trochu divoké, nicméně se nám to v praxi často stává - je to zrovna případ generátoru, kde se točí cívka v magnetickém poli. Ono by to šlo i bez toho, mohli bychom s cívkou spojit souřadnou soustavu a ono by se nám v ní objevilo elektrické pole. Akorát že ta soustava by nebyla inerciální, a běžní lidé (mezi které se počám třeba i já) neví, jak v takové soustavě vypadají zákony elektromagnetismu. Z hlediska pole se ale asi nakonec neděje vůbec nic zvláštního, pole se transformuje dle okamžité rychlosti, jen v každém bodě jinak - protože je v každém bodě jiná rychlost. Ale obecně je jednodušší si to napsat takto.
Offline
#65 17. 11. 2018 11:08
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
Zdá se mi, že tahle obecná definice EMN je ekvivalentní té definici přes práci. Je to tak?
To posoudíme, až ji napíšeš - přesnou formulaci.
V každém případě, když máme teď přesnou definici, můžeme snadno zodpovědět otázky kolem elektromotorického napětí sofistikovaných zdrojů.
Pokud náš zdroj obsahuje chemický článek - a k tomu ještě kupu dalších pasivních součástek, tak celkem snadno ukážeme, že jediný nenulový přírustek podél libovolné smyčky vzniká právě na elektrodách toho chemického článku. Je úplně jedno, jakou smyčku si zvolíme - pokud bude procházet elektrodami chemického článku, dostaneme jeho elektromotorické napětí, pokud bude procházet jinudy, dostaneme mulu.
Z toho můžeme snadno odvodit, za jakých podmínek je napětí na výstupu zdroje rovno jeho elektromotorickému napětí - zřejmě dojdeme k tomu, že když nám tam netečou žádné proudy. Nechce se mi to teď moc do detailu rozebírat, každopádně zdroj obsahující chemický článek a nějaký obvod, který jej zatěžuje, už na výstupu elektromotorické napětí nemá (napětí zdroje naprázdno se nerovná jeho elektromotorickému napětí).
Stejně tak - pokud zdroj obsahuje transformátor, je jeho elektromotorické napětí (za předpokladu, že zvolená smyčka prochází podél sekundárního vinutí) je střídavé. To jsem říkal už na začátku, protože u indukovaného napětí je to celkem zjevné.
Vždy je ale třeba mít na paměti, že elektromotorické napětí závisí na tom, jak si zvolíme tu smyčku, podél které integrujeme. A není až takový problém vymyslet situace, kdy je variant více. Stačí pospojovat pár chemických článků (v sérii s rezistory) PARALELNĚ. Potom si můžeme zovlit smyčku, jež bude procházet kterýmkoliv ze článků - a pro každou volbu dostaneme obecně jiné elektromotorické napětí. Nelze zavést něco jako univerzální elektromotorické napětí takovéto sady.
Stejně tak násobič napětí (složeny z diod a kondenzátorů) mám elektromotorické napětí nezmění. Žádná kombinac e pasivních el. součástek nedokáže zařídit, aby napětí podél uzavřené smyčky bylo nenulové.
Offline
#66 17. 11. 2018 11:13 — Editoval edison (17. 11. 2018 11:16)
Re: Různé napětí - stejný proud?
Mě je ten skalární součin jasný, je to síla zatěžující zdroj mechanického pohybu vodiče přepočtená na jednotkový proud, nebo síla působící na jednotkový náboj, takže je to lorenzova síla pro q=1. Ale zaujalo mě, proč ty ostatní členy mají vytknuto 1/q.
Offline
#67 17. 11. 2018 11:20
Re: Různé napětí - stejný proud?
Ještě je docela zajímavé se zamyslet nad tím, jak to pole galvanického článku vlastně vypadá, a kde že má tu nenulovou rotaci - kterou potřebujeme, abychom dostali nenulový příspěvek podél uzavřené smyčky. A zjistíme celkem zajímavou věc.
Pole se nachází na povrchu elektrody, a z důvodů symetrie lze celkem opravněně předpokládat, že je na její povrch kolmé (kdyby nebylo - jak poznáme, kterým směrem by se u koule mělo sklánět ?). A nenulovou velikost má jen ve velmi tenké vrstvě na povrchu elektrody - vrstvě o tloušťce několika molekul. Je to tedy v podstatě homogenní pole - a takové má rotaci nulovou. Jediné místo, kde rotace nulová není je v místě, kde elektroda vystupuje z elektrolytu. Jen tam - kousek pod hladinou pole je, kousek nad hladinou už není. Celý příspěvek integrálu podél smyčky pochází z tohoto kousku, kde elektroda vystupuje nad hladinu.
Z hlediska výpočtu tak vlastně elektroda nepředstavuje žádný užitek, he.
U elektrického (statického) pole by se nám tohle nikdy nepřihodilo. Taková situace, kdy by pole E pod hladinou bylo a nad hladinou už né - takové el. pole nikdy nevytvoříme. Přesněji tedy - aby vektor E mířil tečně s hladinou. Kolmo na rozhranní se nám to podařit může - ale pak zase nezískáme tu nenulovou rotaci.
Offline
#68 17. 11. 2018 11:27
Re: Různé napětí - stejný proud?
edison napsal(a):
Ale zaujalo mě, proč ty ostatní členy mají vytknuto 1/q.
No protože ta ostaní silová pole (chemické, tepelné) nepůsobí na náboj, ale přímo na částici - dá se říct mechanickým způsobem. Takže to musíme podělit nábojem té částice, abychom získali sílu působící na jednotkový náboj. A tam si také musíme dát pozor na to, že pro částice s nábojem třeba -e dostaneme jiné pole než pro částici s nábojem -2e.
Také bychom to tím nábojem dělit nemuseli, a naopak elektrickou intenzitu E bychom nábojem vynásobili - jenže výsledek by nebyl v jednotkách napětí, ale v jednotkách energie či práce. Protože napětí je práce vztažená na přenos jednotkového náboje.
Offline
#69 18. 11. 2018 03:35
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
To posoudíme, až ji napíšeš - přesnou formulaci.
"Velikost práce, kterou vykonávají vnější síly při přemisťování jednotkového náboje."
Teď si všímám, že EM napětí podle této definice je konstanta pro daný zdroj, zatímco napětí podle definice v ↑ KennyMcCormick: je závislé na konkrétní křivce procházející zdrojem.
Můžu si představit takový zdroj, kde náboj protéká jen po jedné konkrétní křivce a v takovém případě by byly obě definice ekvivalentní.
Takže máme-li zdroj, skrze který po každé křivce (spojující oba póly zdroje) protéká infinitezimální množství náboje, můžu definovat pravděpodobnostní míru na množině všech těchto křivek (úměrnou náboji, který po každé křivce proteče) a střední hodnota takto definovaného EMN by pak měla být rovna hodnotě EMN definovaného prostřednictvím práce. Je to tak?
(Do konkrétních příkladů bych se pustil, až vyřešíme vztah mezi oběma definicemi.)
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#70 18. 11. 2018 12:57
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
To posoudíme, až ji napíšeš - přesnou formulaci.
"Velikost práce, kterou vykonávají vnější síly při přemisťování jednotkového náboje."
Teď si všímám, že EM napětí podle této definice je konstanta pro daný zdroj, zatímco napětí podle definice v ↑ KennyMcCormick: je závislé na konkrétní křivce procházející zdrojem.
Já bych řekl, že ekvivalentní definice je, že to je velikost práce vnějších sil při přenosu náboje podél uzavřené křivky. A pak se nemusíme omezovat na "vnější síly", protože se to těžko posuzuje, co je a co není "vnější síla". Klidně to můžeme vynechat a říct, že je to velikost práce, která je vykonána při přenosu náboje podél uzavřené křivky.
Pokud je možných křivek více - a dávají netriviální hodnoty (tj jiné než nulu nebo EMN), tak to podle mě nemá smysl definovat nějaké "střední EMN", protože stejně nevíme, co to znamená - a obecně bude záviset na tom, co na zdroj připojíme.
Složením vhodných kousků kovu dohromady můžeme třeba vytvořit spalovací motor - a je asi celkem pramálo užitečné zavádět v takovém případě něco jako "průměrný kousek kovu".
Tohle je přesně to, čím se zabývali filozofové - že z pojmu, který dával smysl jen v určité konkrétní situaci se pokoušeli vytvořit pojem univerzální, který bude dávat smysl vždycky. Moc úspěšní s tím ale nebyli...
Nicméně dle teorie obvodů libovolnou kombinaci lineárních prvků (zdroje, odpory, řízené zdroje atd) lze nahradit jedním ideálním zdrojem a jedním sériovým odporem. Stejně dobře to ovšem můžeme nahradit ideálním zdrojem proudu a paralelním odporem. Ekvivalentem je to ovšem pouze z pohledu připojovacích svorek, není to fyzikální ekvivalent.
Dále - nezapomeň, že ta definice by neměla být omezena na statická pole - a pak už je otázka, co tou "prací vykonanou při přenesení náboje" myslíme, protože žádný náboj není možné přenést nekonečně rychle. Nezbude nám, než si tu dráhu rozdělit na malinkaté kousky a počítat to v každém zvlášť. Čímž se dostáváme zpátky k té definici pomocí dráhového integrálu.
Offline
#71 18. 11. 2018 16:57
Re: Různé napětí - stejný proud?
↑ KennyMcCormick:
Také jsi ještě často zmiňoval pojem "neelektrostatické síly". Ale zase, když se nad tím zamyslíme ve světle toho, co už jsme "odhalili", zjistíme, že my vlastně nepotřebujeme "nestaticitu", tj aby dE/dt <> 0, ale potřebujeme aby rot E <> 0.
K tomu bych podotknul, že vektorové pole je celkem plně určené, pokud známe jeho divergenci a rotaci. Je možné, že ještě musíme specifikovat nějakou multiplitkaviní či aditivní konstantu, ale jinak nám to stačí, znát rotaci a divergenci.
Ono se tak nějak mlčky vychází z toho, že když je pole E nestatické, tak musí mít nutně nenulovou rotaci, ale není to až tak úplně pravda. Dají se vymyslet pole, které proměnné jsou, a přitom mají rotaci nulovou. Pořád mluvím o elektromagnetismu, samozřejmě. Pokud budeme například nabíjet kondenzátor (třeba deskový, nebo dvě koule vedle sebe) konstantním proudem, nikdo na světě nemůže tvrdit, že pole mezi elektrodami je konstantní (statické). Ne - bude se v čase lineárně zvětšovat. To možná vyvolá nějaké magnetické pole (ve skutečnosti né, ale to je na jinou kapitolu) - ale tohle magnetické pole bude už v čase konstantní - a tudíž nám žádné indukované napětí (pole s nenulovou rotací) nevytvoří.
Takže takovéto, lineárně narůstající el. pole je určitě "neelektroastatické", ale přitom nám žádné elektromotorické napětí nevytváří. Prostě - ať na to půjdeme z jakékoliv strany, vždycky dojdeme k tomu, že potřebujem pole (či síly) NEKONZERVATIVNÍ, tj silové pole s nenulovou rotací.
Offline
#72 19. 11. 2018 04:47
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
Já bych řekl, že ekvivalentní definice je, že to je velikost práce vnějších sil při přenosu náboje podél uzavřené křivky. A pak se nemusíme omezovat na "vnější síly", protože se to těžko posuzuje, co je a co není "vnější síla". Klidně to můžeme vynechat a říct, že je to velikost práce, která je vykonána při přenosu náboje podél uzavřené křivky.
(To jedno "vnější" je tam asi navíc.) 🙂
Můžeme říct, že je to práce sil při přenosu jednotkového náboje podél uzavřené křivky (procházející póly zdroje a vnitřkem zdroje).
(Btw, může zdroj působit elektromotorickou silou i na náboje mimo zdroj? (Např. v obvodech se střídavým proudem? (Nebo ne?)))
↑ MichalAld:
To možná vyvolá nějaké magnetické pole (ve skutečnosti né, ale to je na jinou kapitolu)
K tomu se někdy později vrátím (v jiném vlákně)...
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#75 19. 11. 2018 15:19
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
(To jedno "vnější" je tam asi navíc.) 🙂
Ale né, to jen ukazuje myšlenkový proces...
KennyMcCormick napsal(a):
Můžeme říct, že je to práce sil při přenosu jednotkového náboje podél uzavřené křivky (procházející póly zdroje a vnitřkem zdroje).
Vnitřek zdroje - to je taky takový přesně definovaný pojem...
Všechno bude fajn, když nebude záležet na tom, kudy smyčka povede. V opačném případě stejně asi žádnou kloudnou a univerzální definici nevymyslíš.
KennyMcCormick napsal(a):
(Btw, může zdroj působit elektromotorickou silou i na náboje mimo zdroj? (Např. v obvodech se střídavým proudem? (Nebo ne?)))
Dosud jsme mluvili o elektromotorickém napětí - a to je nějaká veličina, jež se vztahuje na konkrétní uzavřenou smyčku. Ovšem - pořád mluvíme o obvodech - tj předpokládáme, že ta smyčka vede vnitřkem nějakého vodiče.
Pokud povede smyčka vzduchem - no, není to nic proti ničemu, ale v takových případech už se zpravidla pojem elektromotorického npětí nepoužívá - nikdy jsem například neslyšel o elektromotorickém napětí antény. Ale nicméně takové působení na dálku je samozřejmě možné - můžeš si vyzkoušet vložit žádrovku do mikrovlnné trouby a uvidíš to sám (doporučuji ji tam nenechávat moc dlouho, jen zlomek vteřiny - ona pak bouchne a ty střepy se hrozně blbě uklízí....).
Dále - použil jsi pojem "elektromotorická síla" a já zase tradičně budu otravovat s tím, že nevím, co to vlastně je. Elektromotorické napětí je jasné. Ale pokud jde o sílu - síla působí v jednom konkrétním bodě - a v jednom bodě nepoznáme, jestli je ta síla "elektromotorická" nebo né - nepoznáme, jestli je silové pole konzervativní, nebo není.
Obecně ale střídavé proudy mohou vytvářet elektromagnetické pole, které se šíří prázdným prostorem a může ovlivňovat nabité částice na dálku a předávat jim energii - a dokonce může docházet k vyzařování energie i když tam žádné částice nejsou (el. mag. vlny). A ano - všechno to mohou dělat i zařízení, které jinak využíváme jen jako zdroje napětí. Pokud ovšem elektrické pole nemění svoji velikost, tak k žádnému takovému efektu docházet nemůže.
Offline
