Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 11. 2018 19:33
Olympicke cvicenie
Pozdravujem.
Nech je 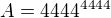 .
. ciferny sucet cisla
ciferny sucet cisla  ,
, ciferny sucet cisla
ciferny sucet cisla  ,
, ciferny sucet cisla
ciferny sucet cisla  .
.
Vypocitajte  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 20. 11. 2018 10:49
Re: Olympicke cvicenie
Offline
#3 22. 11. 2018 01:46
- check_drummer

- Příspěvky: 5168
- Reputace: 106
Re: Olympicke cvicenie
"Máte úhel beta." "No to nemám."
Offline
#4 22. 11. 2018 05:09 — Editoval vanok (22. 11. 2018 07:59)
Re: Olympicke cvicenie
Komentar a jedno riesenie ( bez akejkolvek kalkulacky, ktore su zakazane na olympiadach).
Staci vediet ze
A) sucet cislic daneho prirodzeneho cisla  a cisla
a cisla  maju rovnaky zvysok po deleni cislom 9.
maju rovnaky zvysok po deleni cislom 9.
Co da 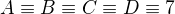 mod 9
mod 9
B) nie je nutne robit presne vypocty, lebo odhady cisiel A, B, C, D postacia
Tak 
 ma menej ako
ma menej ako 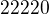 cislic ktore su najviac
cislic ktore su najviac 
Preto  ,
,  ma prvu cislicu najviac
ma prvu cislicu najviac  a ostatne najviac
a ostatne najviac 
co sa 
Podobne 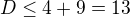
C) Akoze mod 9 existuje jedine cislo mensie ako 13 a rovne cislu 7, mame 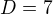
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 27. 11. 2018 12:09
Re: Olympicke cvicenie
Pozdravujem ↑ Honzc:,
Mysli na kriterium delitelnosti cislom 9.
Potrebujes podrobny dokaz?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 28. 11. 2018 13:34
Re: Olympicke cvicenie
Ahoj ↑ Honzc:,
Tak dobre., napisem ti viac podrobnosti, zo zaciatkom dokazu.
Co sa tyka 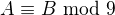 (1) to ti urcite jasne, ze.
(1) to ti urcite jasne, ze.
Primeniem este dalsiu velmi znamu vlasnost
Ak mame pre cele cisla 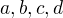 take, ze
take, ze 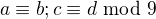 potom
potom 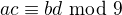
. (2)
Tak mas vdaka (1), 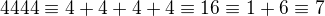
A zvysok vdaka (2):
Najprv 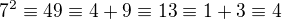
Potom 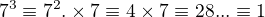
A tiez 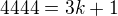
Staci?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline