Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 11. 2018 17:45 — Editoval Peterslovak (22. 11. 2018 17:52)
- Peterslovak
- Příspěvky: 270
- Škola: gymnázium
- Pozice: student
- Reputace: 3
Komplexne cisla
Dobry vecer, mohli by ste mi pomoct s tymito dvomi prikladmi? V prvom mi vychádza t^2>-16. Co s tym dalej?
1.) x^2 + (t-4)x - 2t = 0
2.) (5t+1)x^2 + (7t+3)x + 3t = 0
Pre ktoré t∈R majú nasledujúce rovnice dva reálne a pre ktoré dva imaginárne korene?
„Představivost je důležitější než vědomosti.“- Albert Einstein
Offline
#2 22. 11. 2018 17:53 — Editoval Jj (22. 11. 2018 17:54) Příspěvek uživatele Jj byl skryt uživatelem Jj.
#4 22. 11. 2018 18:15
- Peterslovak
- Příspěvky: 270
- Škola: gymnázium
- Pozice: student
- Reputace: 3
Re: Komplexne cisla
po uprave z: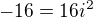
??
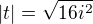
„Představivost je důležitější než vědomosti.“- Albert Einstein
Offline
#5 22. 11. 2018 18:15 — Editoval misaH (22. 11. 2018 18:19)
- misaH
- Příspěvky: 13459
Re: Komplexne cisla
↑ Peterslovak:
Podľa mňa to komplikuješ.
Otázka je jasná.
Pre ktoré reálne t má rovnica 2 rôzne reálne korene.
No pre to t, pre ktoré je D kladný.
A pre ktoré reálne t má rovnica komplexné korene?
No pre to t, pre ktoré je D<0.
To je všetko.
Offline
#6 22. 11. 2018 18:17
- Peterslovak
- Příspěvky: 270
- Škola: gymnázium
- Pozice: student
- Reputace: 3
Re: Komplexne cisla
D<0 ?
„Představivost je důležitější než vědomosti.“- Albert Einstein
Offline
?#8 22. 11. 2018 18:19
- Peterslovak
- Příspěvky: 270
- Škola: gymnázium
- Pozice: student
- Reputace: 3
Re: Komplexne cisla
t∈R
„Představivost je důležitější než vědomosti.“- Albert Einstein
Offline
#9 22. 11. 2018 18:21
- misaH
- Příspěvky: 13459
Re: Komplexne cisla
↑ Peterslovak:
No vidíš...
Takže rovnica 1 má vždy D>0, takže má (podľa mňa, snáď sa nemýlim) vždy 2 reálne korene.
Offline
#10 22. 11. 2018 18:27
- Peterslovak
- Příspěvky: 270
- Škola: gymnázium
- Pozice: student
- Reputace: 3
Re: Komplexne cisla
V riešeniach mám napísané že má 2 reálne ak 
, dva imaginarne ak 
, dvojnasobny ak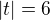 
„Představivost je důležitější než vědomosti.“- Albert Einstein
Offline
#12 22. 11. 2018 18:31
- Peterslovak
- Příspěvky: 270
- Škola: gymnázium
- Pozice: student
- Reputace: 3
Re: Komplexne cisla
Ale proc zrovna 6?
„Představivost je důležitější než vědomosti.“- Albert Einstein
Offline
#13 22. 11. 2018 18:34 — Editoval misaH (22. 11. 2018 18:35)
- misaH
- Příspěvky: 13459
Re: Komplexne cisla
↑ Peterslovak:
Veď si to napísal:
V riešeniach mám napísané že má 2 reálne ak
Tak skontroluj to posledné tvrdenie, teda že pre |t|=6 (teda t=6 alebo t=-6) vychádza jeden dvojnásobný koreň.
Dosádzať mínus 6 by sa mi nechcelo, skontrolovala by som radšej najprv t=6.
Offline
#14 22. 11. 2018 18:43
- Peterslovak
- Příspěvky: 270
- Škola: gymnázium
- Pozice: student
- Reputace: 3
Re: Komplexne cisla
Dosadil som do povodnej rovnice za t cislo 6 a vysiel mi diskriminant 52, co mi neda 1 dvojnasobny koren
„Představivost je důležitější než vědomosti.“- Albert Einstein
Offline
#15 22. 11. 2018 18:51 — Editoval misaH (22. 11. 2018 18:53)
- misaH
- Příspěvky: 13459
Re: Komplexne cisla
↑ Peterslovak:
Tak vidíš.
Nedá sa vždy veriť tomu, čo je napísané...
Offline
nedává smysl. Pomocí symbolů „menší (nebo rovno)“ a „větší (nebo rovno)“ můžeme porovnávat jen reálná čísla.