Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#76 21. 11. 2018 01:37
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
Obecně ale střídavé proudy mohou vytvářet elektromagnetické pole, které se šíří prázdným prostorem a může ovlivňovat nabité částice na dálku a předávat jim energii - a dokonce může docházet k vyzařování energie i když tam žádné částice nejsou (el. mag. vlny). A ano - všechno to mohou dělat i zařízení, které jinak využíváme jen jako zdroje napětí. Pokud ovšem elektrické pole nemění svoji velikost, tak k žádnému takovému efektu docházet nemůže.
To je vlastně pravda. Takže kdybych měl obvod se střídavým proudem, působil by zdroj silou i na náboje v jiných částech obvodu, je to tak?
Dále - použil jsi pojem "elektromotorická síla" a já zase tradičně budu otravovat s tím, že nevím, co to vlastně je. Elektromotorické napětí je jasné. Ale pokud jde o sílu - síla působí v jednom konkrétním bodě - a v jednom bodě nepoznáme, jestli je ta síla "elektromotorická" nebo né - nepoznáme, jestli je silové pole konzervativní, nebo není.
Proč ne? Nemůžeme od celkového pole odečíst konzervativní pole, nekonzervativní pole nezpůsobená zdrojem a být zanecháni s elektromotorickým polem?
(Mimochodem, napadlo mě, že elektromotorické pole může být v rámci zdroje konzervativní (i když ve skutečnosti asi není), protože my potřebujeme pouze nekonzervativnost v prostoru "vnitřek zdroje + zbytek obvodu", nikoliv nekonzervativnost v prostoru "vnitřek zdroje".)
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#77 21. 11. 2018 19:31
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
To je vlastně pravda. Takže kdybych měl obvod se střídavým proudem, působil by zdroj silou i na náboje v jiných částech obvodu, je to tak?
Áno, a také se to dost často stává, že nám, zejména při vyšších frekvencích vznikají v obvodech vazby, které jsme nezamýšleli a které tam nechceme. Může jít jako o působení elektrické (kapacitní) tak i magnetické (indukční) a při vyšších frekvencích i o elektromagnetické vyzařování.
K tomu bych ještě připoměl, že celá teorie obvodů stojí na tom, že se signály šíří "nekonečně rychle". V obvodech střídavého proudu vystupuje čas, ale né poloha. To platí jen pokud použitý kmitočet je dostatečně nízký - rozměry obvodu jsou mnohem větší než vlnová délka odpovídající frekvence. Pokud to tak není, tak se to musí analyzovat a zejména navrhovat úplně jinak. Šíření signálu kabelové televize nebo ethernetu se už těmi jednoduchými principy neřídí - tam už musíme použít vlnovou rovnici (telegrafní rovnice).
A to samé platí o elektromotorickém napětí - pokud začnou být rozměry té smyčky srovnatelné nebo větší s vlnovou délkou použité frekvence, tak se to bude chovat mnohem zajímavějším způsbem, než jsme zvyklí - napětí se bude periodicky měnit pokaždé když rozměr smyčky dosáhne n-násobku délky vlny.
KennyMcCormick napsal(a):
Dále - použil jsi pojem "elektromotorická síla" a já zase tradičně budu otravovat s tím, že nevím, co to vlastně je. Elektromotorické napětí je jasné. Ale pokud jde o sílu - síla působí v jednom konkrétním bodě - a v jednom bodě nepoznáme, jestli je ta síla "elektromotorická" nebo né - nepoznáme, jestli je silové pole konzervativní, nebo není.
Proč ne? Nemůžeme od celkového pole odečíst konzervativní pole, nekonzervativní pole nezpůsobená zdrojem a být zanecháni s elektromotorickým polem?
(Mimochodem, napadlo mě, že elektromotorické pole může být v rámci zdroje konzervativní (i když ve skutečnosti asi není), protože my potřebujeme pouze nekonzervativnost v prostoru "vnitřek zdroje + zbytek obvodu", nikoliv nekonzervativnost v prostoru "vnitřek zdroje".)
1) Už jsem to zmínil jednou, když už máme pole, neměly bychom se starat o to, co nám tohle pole vytvořilo. Takže nějaké "pole nezpůsobené zdrojem" bychom měli ze svých úvah vynechat.
2) Můžeme od celkového pole odečíst nějaké konzervativní pole, otázka ovšem je, jestli to lze provést jednoznačně. Nejlépe to pochopíš, když si to sám zkusíš na nějakém příkladě.
3) "elektromotorické pole" je pojem, který nejspíš nic neznamená.
4) Pokud jde o tu nekonzervativnost - pokud do úlohy zahrneme opravdu všechny síly, tak jsou vždycky konzervativní. Žádné nekonzervativní síly v našem vesmíru neexistují. Nekonzervativnost je vždycky výsledkem toho, že bereme v úvahu vždy jen část našeho světa.
Na závěr malou ukázku - představ si el. pole jehož siločáry tvoří soustředné kružnice, stejně jako magnetické pole kolem (nekonečně) tenkého vodiče (jako tady). Na první pohled je zřejmé, že pole je nekonzervativní, integrál po každé z těch kružnic dává nenulovou hodnotu (vždy stejnou, mmch).
Pokud se ale pokusíme zjistit, kde přesně se ta nekonzervativnost nachází, začne to být zajímavé. Prostě - pokud nám smyčka neobtáčí střed, tak má EMN = 0, pokud střed obtáčí, tak je rovné nějaké hodnotě.
Když se spočítáme rotaci toho pole (v každém bodě) tak zjistíme, že je všude nulová, jen ve středu těch kruhů neexistuje. Ten jediný bod může za tu nekonzervativnost.
Konzervativnost je prostě taková "nelokální vlastnost". Z nějaké části toho pole nepoznáme, jestli je nebo není.
Offline
#78 25. 11. 2018 16:38 — Editoval KennyMcCormick (25. 11. 2018 16:47)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
3) "elektromotorické pole" je pojem, který nejspíš nic neznamená.
To je prostor, ve kterém působí síly, kterými je realizovaná elektromotorické síla. Takže pokud budeme definovat![kopírovat do textarea $\mathcal{E}\equiv\oint\limits_\mathcal{C}[\textbf{E}+\textbf{v}\times\textbf{B}]\d\textbf{l}+\frac1 q\oint\limits_\mathcal{C}(\text{efektivní chemické síly})\d\textbf{l}+\frac1 q\oint\limits_\mathcal{C}(\text{efektivní termální síly})\d\textbf{l}$](/mathtex/d9/d9364e20275dc4805161a69fcd0682bb.gif) , tak elektromotorická síla se skládá z
, tak elektromotorická síla se skládá z 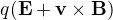 , efektivních chemických sil a efektivních termálních sil.
, efektivních chemických sil a efektivních termálních sil.
Vím, že konzervativnosti je otázka celého pole, ne konkrétního bodu. 🙂
Mě by zajímal tenhle zjednodušený příklad:
Mějme obvod se zdrojem stejnosměrného napětí, jehož póly mají potenciál  a
a  a který přesouvá náboj pouze po jedné konkrétní křivce
a který přesouvá náboj pouze po jedné konkrétní křivce 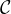 . Elektrické pole způsobené póly zdroje (
. Elektrické pole způsobené póly zdroje ( ) je konzervativní.
) je konzervativní.
Vnitřkem zdroje přesune zdroj náboj  ze záporného pólu zdroje na kladný po křivce
ze záporného pólu zdroje na kladný po křivce 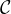 .
.
V každém bodě této křivky na náboj působí elektrická síla o velikosti  , ve směru vektoru
, ve směru vektoru  . Takže v každém bodě bude zdroj působit silou o velikosti
. Takže v každém bodě bude zdroj působit silou o velikosti  ve směru
ve směru  .
.
Práce vykonaná zdrojem je . Je to tak?
. Je to tak?
Edit: Přidáno "a který přesouvá náboj pouze po jedné konkrétní křivce 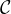 "
"
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#79 25. 11. 2018 16:48
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
3) "elektromotorické pole" je pojem, který nejspíš nic neznamená.
To je prostor, ve kterém působí síly, kterými je realizovaná elektromotorické síla. Takže pokud budeme definovat
, tak elektromotorická síla se skládá z
, efektivních chemických sil a efektivních termálních sil.
Já bych uvítal, kdybys používal pojmy, které jsou ve fyzice běžné, a nevymýšlel zbytečně nové, zejména když z toho není žádný užitek. Konkrétně "pole je prostor, který..." - pole není prostor, pole je funkce prostorových (časoprostorových) souřadnic. Může to být skalární funkce (pak je to skalární pole) nebo vektorová funkce (vektorové pole) atd.
Takže stačí říct silové pole - případně, pokud bez toho nemůžeš žít, tak pole elektromotorických sil.
Offline
#80 25. 11. 2018 16:54 — Editoval MichalAld (25. 11. 2018 17:01)
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
Vnitřkem zdroje přesune zdroj náboj
ze záporného pólu zdroje na kladný po křivce
.
Je otázka, jestli se fyzický náboj bude přesouvat zrovna ze záporného pólu na kladný, ale v rámci teorie obvodů je to jedno.
KennyMcCormick napsal(a):
V každém bodě této křivky na náboj působí elektrická síla o velikosti
,
To je hodně obecně řečeno - "o velikosti E", "velikost E" může být cokoliv.
V každém případě - tam, kde bude vnitřek zdroje tvořen vodiči, bude tato síla nulová.
Zbytek je asi v pořádku. Až na jednu malou, ale důležitou věc. Pro pole E musí platit rot E = 0, jinak ty elektrické potenciály nemůžeme používat. Ale pokud tam nebude žádné jiné el. pole než to vytvořené póly zdroje, tak je to OK.
Offline
#81 27. 11. 2018 22:56
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
pole není prostor, pole je funkce prostorových (časoprostorových) souřadnic
To je totéž. Pole je oblast prostoru, pro kterou platí, že v každém bodě působí na částici s odpovídajícím nábojem síla, a zároveň je to funkce časoprostorových souřadnic. (Kdybys chtěl, můžu to najít v nějakých učebnicích.)
(Máš pravdu, že můžu mít i pole, ve kterých nepůsobí na testovací částici síla (např. teplotní pole), ale v tomhle případě mluvíme o silových polích, tak jsem to nechtěl brát takhle obecně.)
Může to být skalární funkce (pak je to skalární pole) nebo vektorová funkce (vektorové pole) atd.
Ano.
↑ MichalAld:
Je otázka, jestli se fyzický náboj bude přesouvat zrovna ze záporného pólu na kladný, ale v rámci teorie obvodů je to jedno.
Ano, fyzický náboj se bude pohybovat opačným směrem.
To je hodně obecně řečeno - "o velikosti E", "velikost E" může být cokoliv.
 je intenzita elektrického pole v daném bodě, tj.
je intenzita elektrického pole v daném bodě, tj.  je velikost této intenzity v daném bodě.
je velikost této intenzity v daném bodě.
V každém případě - tam, kde bude vnitřek zdroje tvořen vodiči, bude tato síla nulová.
Elektrická síla bude v těchto částech zdroje nulová? Takže když jsi předtím psal, že integrál  skrz zdroj není nulový, tak jsi to myslel tak, že nenulová hodnota integrálu je způsobena těmi částmi, které nejsou vnitřkem vodiče?
skrz zdroj není nulový, tak jsi to myslel tak, že nenulová hodnota integrálu je způsobena těmi částmi, které nejsou vnitřkem vodiče?
(Chápu to správně, že v ideálním vodiči není (pokud budeme předstírat, že se změny v  šíří nekonečně rychle) žádné
šíří nekonečně rychle) žádné  ?)
?)
Pro pole E musí platit rot E = 0, jinak ty elektrické potenciály nemůžeme používat.
Ale asi to není potřeba v celém prostoru, protože na obrázku s naším obvodem se v levé polovině mění  , a zároveň má horní pól potenciál o 33V vyšší než spodní pól (nebo není potenciál definovaný ani v tomhle případě, a je to jenom napětí 33V?)
, a zároveň má horní pól potenciál o 33V vyšší než spodní pól (nebo není potenciál definovaný ani v tomhle případě, a je to jenom napětí 33V?)
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#82 27. 11. 2018 23:36
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
V každém případě - tam, kde bude vnitřek zdroje tvořen vodiči, bude tato síla nulová.
Elektrická síla bude v těchto částech zdroje nulová? Takže když jsi předtím psal, že integrál
skrz zdroj není nulový, tak jsi to myslel tak, že nenulová hodnota integrálu je způsobena těmi částmi, které nejsou vnitřkem vodiče
Né, myslel jsem to prostě jen tak, že pokud ta trasa povede vnitřkem vodiče, tak tam bude E=0. V případě chemického zdroje je to skoro všude - uvnitř elektrod i uvnitř elektrolytu. Jediné místo, kde je nenulové E je velmi tenká vrstva na povrchu elektrod.
KennyMcCormick napsal(a):
(Chápu to správně, že v ideálním vodiči není (pokud budeme předstírat, že se změny v
šíří nekonečně rychle) žádné
?)
Jo. Má to jistá omezení, zejména nesmí vodičem protékat žádný velký proud (nebo musí mít vodič velmi malý odpor) - ale pro začátek je velmi dobré si tohle uvědomit. Ve vodiči nemůže existovat el. pole - uvedlo by do pohybu volné náboje - a ty by se přesouvaly tak dlouho, dokud by pole nezmizelo - sami totiž vytvářejí své vlastní pole - která v ustáleném stavu vyruší to původní. A změny klidně necháme šířit jen rychlostí světla. Důležité je jen to, aby bylo ve vodiči dostatek volných nábojů. V kovu je jich opravdu dostatek.
(určitě se za chvíli najde někdo, kdo to bude rozporovat...ale tím se nenench odradit)
KennyMcCormick napsal(a):
Pro pole E musí platit rot E = 0, jinak ty elektrické potenciály nemůžeme používat.
Ale asi to není potřeba v celém prostoru, protože na obrázku s naším obvodem se v levé polovině mění
, a zároveň má horní pól potenciál o 33V vyšší než spodní pól (nebo není potenciál definovaný ani v tomhle případě, a je to jenom napětí 33V?)
Jestli to musí platit v celém prostoru .... to je zajímavá otázka. Abychom mohli používat představu potenciálu (a tedy i napětí), nesmí výsledek záviset na integrační cestě, kterou si zvolíme. Ale nic nám obecně nebrání si říct, že v jisté části prostoru si integrační cesty volit nebudeme - a v té části prostoru to potom platit nemusí (to rot E = 0). Ale v té části, kde to neplatí, pak nemůžeme používat představu napětí.
No a problém může snadno vzniknout, pokud ta část prostoru, kde to platí, nebude jednoduše souvislá. Ve 2D by stačilo, aby rot E = 0 nebylo splněno v jediném bodě - a čára obkličující tento bod bude dávat jinou hodnotu napětí než čára mimo tento bod.
Když si uvědomíš, jak se měří napětí, bude ti to hned jasné. Vezmeme dva hroty - od kterých vedou vodiče až k měřáku - a přiložíme je na nějaké dva kovové vývody zdroje. A určitě by se ti nelíbilo, když by naměřená hodnota závisela na tom, kudy vedou ty dráty od měřících hrotů k voltmetru.
Při měření vysokofrekvenčních napětí se ti to ovšem velmi často stává, vlastně úplně vždycky - představa, že budeš měřit sinusové napětí o kmitočtu 100 nebo 1000 Mhz dvěma dráty vedoucími k měřáku je úplně nesmyslná.
Offline
#83 28. 11. 2018 01:04
Re: Různé napětí - stejný proud?
MichalAld napsal(a):
Při měření vysokofrekvenčních napětí se ti to ovšem velmi často stává, vlastně úplně vždycky - představa, že budeš měřit sinusové napětí o kmitočtu 100 nebo 1000 Mhz dvěma dráty vedoucími k měřáku je úplně nesmyslná.
Já bych tuhle představu úplně nezatracoval:-) Jen je potřeba, aby měřák i dráty splňovaly určité netriviální podmínky. Proto osciloskop do 10 GHz stojí pár desítek mega a sonda (včetně kabelu) k němu určená, desítky tisíc.
Offline
#84 28. 11. 2018 18:22 — Editoval MichalAld (28. 11. 2018 18:23)
Re: Různé napětí - stejný proud?
↑ edison:
Do 4GHz (20 Gsamples/s) stojí jen asi 700KKC...https://www.rohde-schwarz.com/us/produc … 91808.html
Offline
#85 29. 11. 2018 03:08 — Editoval KennyMcCormick (29. 11. 2018 04:38)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
Takže když jsi předtím psal, že integrál
skrz zdroj není nulový, tak jsi to myslel tak, že nenulová hodnota integrálu je způsobena těmi částmi, které nejsou vnitřkem vodiče
Né, myslel jsem to prostě jen tak, že pokud ta trasa povede vnitřkem vodiče, tak tam bude E=0.
To je totéž - "pokud se bod nachází uvnitř vodiče, pak  ".
".
(nebo musí mít vodič velmi malý odpor)
To je jasné, protože Ohmův zákon se na mikroskopické úrovni odvozuje tak, že mezi srážkami na vodivostní elektrony působí  , takže v případě přítomnosti odporu musí být ve vodiči
, takže v případě přítomnosti odporu musí být ve vodiči  .
.
Ve vodiči nemůže existovat el. pole - uvedlo by do pohybu volné náboje (...)
Tohle vysvětluje jenom to, proč ve stacionárním stavu (a pro 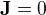 ) není ve vodiči elektrické pole, ne to, proč není v ideálním vodiči elektrické pole za žádných podmínek.
) není ve vodiči elektrické pole, ne to, proč není v ideálním vodiči elektrické pole za žádných podmínek.
Ale tohle jsem četl i z jiných zdrojů, takže ti věřím. 🙂
(Edit: Btw, pokud by někomu vrtalo hlavou (jako mě), co se děje v situacích s nestacionárním proudem, tak v ideálním vodiči může existovat nenulové  , dokud se elektrony nepřeskupí, aby ho vyrušily. I v případě stacionárního proudu může být nenulové
, dokud se elektrony nepřeskupí, aby ho vyrušily. I v případě stacionárního proudu může být nenulové  , pokud je drát (ideální vodič) zahnutý (aby elektrony mohly v drátu zatáčet). Abychom mohli mít skutečně nulové
, pokud je drát (ideální vodič) zahnutý (aby elektrony mohly v drátu zatáčet). Abychom mohli mít skutečně nulové  za všech okolností (s výjimkou nekonečně krátkého okamžiku, kdy se náboje přeskupí, aby mohly toto
za všech okolností (s výjimkou nekonečně krátkého okamžiku, kdy se náboje přeskupí, aby mohly toto  vykompenzovat), museli bychom mít nehmotné náboje, nikoliv elektrony.)
vykompenzovat), museli bychom mít nehmotné náboje, nikoliv elektrony.)
Jestli to musí platit v celém prostoru .... to je zajímavá otázka. Abychom mohli používat představu potenciálu (a tedy i napětí), nesmí výsledek záviset na integrační cestě, kterou si zvolíme. Ale nic nám obecně nebrání si říct, že v jisté části prostoru si integrační cesty volit nebudeme - a v té části prostoru to potom platit nemusí (to rot E = 0). Ale v té části, kde to neplatí, pak nemůžeme používat představu napětí.
Teď bych představil druhý příklad:
V prvním případě (to je ten, který jsem napsal v ↑ KennyMcCormick:) je elektrické pole statické, a náboj je přesunutý neelektrickou silou. Vykonaná práce je rovna napětí na zdroji.
Ve druhém případě bude náboj přesouvaný elektrickou silou po stejné trajektorii. Elektrické pole se už v čase mění, ale jen následkem toho, že zdroj působí na náboj silou, která je elektrická (nebo silou, jejiž jedna složka je elektrická). V každém bodě trajektorie je síla stále stejná jako v předchozím případě, jen se liší její druh (neelektrická => elektrická). Takže i vykonaná práce při přemístění jednotkového náboje by měla být stejná, přestože se celkové elektrické pole (vzniklé složením statického pole tvořeného póly zdroje a proměnného pole tvořeného zdrojem samotným) mění v čase. Je to tak?
(Obecně: není mi jasné, jak může zdroj při přesunu jednotkového náboje mezi póly na obrázku vykonat jakouliv jinou práci než 33J, aniž bys vytvořil perpetuum mobile.)
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#86 29. 11. 2018 21:55
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
. Abychom mohli mít skutečně nulové
za všech okolností (s výjimkou nekonečně krátkého okamžiku, kdy se náboje přeskupí, aby mohly toto
vykompenzovat), museli bychom mít nehmotné náboje, nikoliv elektrony.)
Pokud na elektrony ve vodiči budeme koukat jako na harmonický oscilátor (je to takový ten univerzitní zákon - že vše lze modelovat linární diferenciání rovnicí druhého řádu...) tak tu rychlost reakce neurčuje jen hmotnost elektronů, ale také tuhost té pružiny - elektrického pole, které se vytváří při vychýlení elektronů z jejich rovnovážných poloh.
A mezní kmitočet závisí na obojím, čím nižší hmotnost, a čím vyšší tuhost - tuhost je určená koncentrací těch elektronů a konstantami el. pole. No a dokud jsem hluboko pod mezním kmitočtem, tak se tam žádné znatelné "zpoždění" neprojevuje. Otázka je, jak je ten mezní kmitočet vysoký. Ale minimálně na kmitočtu 100GHz se vodič ještě stále chová jako standarvní vodič. A je klidně možné, že ještě i pro řádově vyšší kmitočty se tak chovat bude - možná i pro kmitočty odpovídající viditelnému světlu se stále ještě chová jako vodič - jinak by světlo tak hezky vodiče neodrážely. Ale je možné, že na těchto kmitočtech se už uplaťňují jiné mechanismy, na úrovni atomů. Alespoň z části.
Takže pro nějaké běžné obvody, o kterých se tady bavíme, je tahle představa více než vyhovující.
Tady je asi vhodný bod si uvědomit, že žádný fyzikální zákon nepopisuje náš svět úplně přesně. Vše je jen nějaké zjednodušení - o tom celá fyzika je. A i když máme zákony, které považujeme za úplně správné (snad kvantová teorie elektromagnetického pole) tak je v nějakých složitějších případech nedokážeme použít a musíme si vymyslet nějaké jednodušší modely).
Co chci říct - že zatímco tady do subtilních detailů řešíme, jestli je ve vodiči nulové E i v případě střídavého napětí - přitom třeba samotné Maxwellovy rovnice nejsou správným modelem pro střídavé napětí (střídavá pole). A to tě třeba vůbec netrápí.
U viditelného světla se už jednoznačně projevuje jeho kvantová povaha - zatímco představa nulového E ve vodiči může i na světelných frekvencích fungovat ještě docela dobře.
Já ze zkušenosti vím, že spousta lidí nemá představu nulového E ve vodiči vůbec zažitou - nakonec i ty sám jsi odkazoval nějakou učebnici, kde bylo zmíněno E v celém objemu elektrolytu chemického článku - což je úplný nesmysl. Stejně tak má někdo problém při popisu transformátoru, že ve vodiči je E = 0. Jasně, je to zjednodušení, ale né principiální. Je to nakonec docela dobré přiblížení - a pokud dodržíme vhodné podmínky - aby nám tam netekly moc velké proudy, je dobré minimálně do stovek GHz. A možná i mnohem dál.
Offline
#87 29. 11. 2018 21:59
Re: Různé napětí - stejný proud?
Také jsi zmiňoval nějaké nenulové E když nám vodič zatáčí.
To ale mmch také nemusí být pravda. Ono nám tam vzniká také ještě i magnetické pole, a to se obecně snaží udržet proud jaký je, a nejen co do velikosti, ale někdy i co do směru.
Vzpomínám si, že lze vytvořit plazmové útvary co vypadají trochu jako šroubovice (jako pružina...) - a jsou v podstatě stabilní. Je to prostě výboj ve tvaru spirály - a proud částic je držen pohromadě jen magnetickým polem, co proud vytváří. Není tam žádná izolace která by určovala, kudy se má proud ubírat. Respektive je (okolní vzduch není úplně vodivý) ale je to plyn - výboj by se klidně mohl někam přesouvat, narovnat se nebo tak - ale on je celkem dlouhodobě stabilní. Je to ale jen jedna speciální stabilní konfigurace.
Offline
#89 05. 12. 2018 02:02
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
Takže pro nějaké běžné obvody, o kterých se tady bavíme, je tahle představa více než vyhovující.
Ano. 🙂
Tady je asi vhodný bod si uvědomit, že žádný fyzikální zákon nepopisuje náš svět úplně přesně.
Ano. (Je zajímavé, že kvantová fyzika popisuje náš svět úplně přesně v limitě gravitačního pole jdoucího k nule (pokud vím).)
Já ze zkušenosti vím, že spousta lidí nemá představu nulového E ve vodiči vůbec zažitou - nakonec i ty sám jsi odkazoval nějakou učebnici, kde bylo zmíněno E v celém objemu elektrolytu chemického článku - což je úplný nesmysl.
Detail: Oni právě psali, že celkové E je nula, a ty jsi psal, že vnitřkem zdroje je nenulový integrál E (což implikuje nejméně jeden bod s nenulovým E).
(Ale to jsme si už vyjasnili.)
↑ MichalAld:
Také jsi zmiňoval nějaké nenulové E když nám vodič zatáčí.
To ale mmch také nemusí být pravda. Ono nám tam vzniká také ještě i magnetické pole, a to se obecně snaží udržet proud jaký je, a nejen co do velikosti, ale někdy i co do směru.
Aha. 🙂
Když budu mít ohnutý ideální vodič, nebude hustota magnetických siločar ve vnější části zatáčky nižší než ve vnitřní části (a jestli ano, nebude to mít za následek, že proud bude tlačen ven více než dovnitř)?
Vzpomínám si, že lze vytvořit plazmové útvary co vypadají trochu jako šroubovice (jako pružina...) - a jsou v podstatě stabilní. Je to prostě výboj ve tvaru spirály - a proud částic je držen pohromadě jen magnetickým polem, co proud vytváří. Není tam žádná izolace která by určovala, kudy se má proud ubírat. Respektive je (okolní vzduch není úplně vodivý) ale je to plyn - výboj by se klidně mohl někam přesouvat, narovnat se nebo tak - ale on je celkem dlouhodobě stabilní. Je to ale jen jedna speciální stabilní konfigurace.
To je zajímavé - myslel jsem, že to magnetické pole musí být udržované vnějších zdrojem. 🙂
↑ MichalAld:
Tohle moc nechápu, asi budeš muset nějak srozumitelněji. Vztahuje se to k něčemu dřívějšímu?
Ne nezbytně.
Obecně, mějme DC zdroj, uvnitř kterého zdroj púsobí na náboj silou, jejíž jedna složka je elektrická, a tahle síla závisí na čase (takže v konečném důsledku, pokud síly, kterými zdroj působí, znázorníme pomocí pole, tak jedna složka pole bude střídavé E). Ale protože zdroj nepohybuje nábojem ve střídavém poli, ale pohybuje jím v konstantním poli proměnnou silou, nebude fakt, že jedna složka této síly je proměnná elektrická síla, mít vliv na práci vykonanou zdrojem.* (Vliv by to mělo, pouze pokud by to střídavé pole bylo způsobené něčím jiným, a nebylo by pouze znázorněním proměnné síly zdroje.)
(Předtím jsi psal, že bychom neměli mluvit o "poli způsobeném zdrojem", ale v tomhle případě o něm mluvit musíme, protože mluvíme o práci vykonané zdrojem, což vyžaduje sílu působící zdrojem po dráze, tuto sílu můžeme zapsat jako pole (vydělením síly jednotkovým nábojem).)
*Proto jsem psal:
(Obecně: není mi jasné, jak může zdroj při přesunu jednotkového náboje mezi póly na obrázku vykonat jakouliv jinou práci než 33J, aniž bys vytvořil perpetuum mobile.)
(což už se vztahuje k našemu obvodu na obrázku).
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#90 05. 12. 2018 10:18
Re: Různé napětí - stejný proud?
↑ KennyMcCormick:
Tato diskuze je pro mně moc oduševnělá a moc jsem ji nezkoumal, dovolím si zareagovat jen na dvě věci z posledního příspěvku:
Když budu mít ohnutý ideální vodič, nebude hustota magnetických siločar ve vnější části zatáčky nižší než ve vnitřní části (a jestli ano, nebude to mít za následek, že proud bude tlačen ven více než dovnitř)?
Ano, bude. Právě jsi popsal jednu z mnoha nestabilit v plazmatu, která utlumila počáteční optimismus při výzkumu fúze. Konkrétně je to kink instability. Viz např. obrázek.
To je zajímavé - myslel jsem, že to magnetické pole musí být udržované vnějších zdrojem.
V plazmatu se celkově různé věci chovají zvláštně. Doporučuji knížku Úvod do teorie plazmatu od Petra Kulhánka, kde se o tomto mluví. Zejména jde o oddíly 3.1.2. (Rovnice pro magnetické pole) a 3.2.3. (Helicita). V páté kapitole se mluví i o těch nestabilitách, ale to je jen pro trpělivé.
Offline
#91 08. 12. 2018 21:48
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
(Obecně: není mi jasné, jak může zdroj při přesunu jednotkového náboje mezi póly na obrázku vykonat jakouliv jinou práci než 33J, aniž bys vytvořil perpetuum mobile.)
Já už asi trochu chápu, co tě trápí. Ona se práce 33J vykoná, při přenosu jednotkového náboje, jenže k přenosu náboje nedochází konstantní rychlostí (proudem).
Pokud chceme mluvit o napětí proměnném v čase, musíme si vymyslet lepší definici než přenos jednotkového (nebo ji jakéhokoliv jiného) náboje od jednoho pólu ke druhému - protože náboj nedokážeme přenášet nekonečně rychle.
Musíme používat takovou definici napětí, abychom ho dokázali stanovit v nekonečně krátkém čase. A nepředpokládám, že vymyslíš něco lepšího než dráhový integrál E, kde E lze definovat klidně jako U/d, jenže to d je nekonečně malé, takže není až takový problém náboj přenést nekonečně rychle. Nebo můžeme E definovat podle síly působící na náboj, jenže sílu poznáme také jen tak, že nám těleso během pohybu po dráze d změní rychlost (hybnost).
Offline
#92 09. 12. 2018 00:48 — Editoval KennyMcCormick (09. 12. 2018 00:49)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
Ona se práce 33J vykoná, při přenosu jednotkového náboje
OK. 🙂
jenže k přenosu náboje nedochází konstantní rychlostí (proudem).
Pokud chceme mluvit o napětí proměnném v čase
Ah - ale napětí mezi póly DC zdroje se nemění - je to stále 33V. (Abych si byl 100% jistý, že si rozumíme - práce vykonaná zdrojem při přesunu jednotkového náboje je definice (jedna z definic) EM napětí - ne nezbytně jakéhokoliv napětí. Takže to, že se uvnitř zdroje samotného mění napětí mezi různými dvojicemi bodů (protože tam je i AC zdroj) nemusí nezbytně vadit.)
Takže teď se (snad) shodujeme, že pokud definujeme EM napětí jako práci vykonanou zdrojem při přesunu jednotkového náboje, všechny ideální DC zdroje mají EM napětí rovny napětí na svorkách.
Co se týče DC zdroje s proměnným E ve svém vnitřku, kde se náboj přenáší jen po jediné křivce, není v každém okamžiku  křivkový integrál (pokud definujeme EM napětí tímhle křivkovým integrálem: ↑ KennyMcCormick:) roven práci vykonané při přesunu jednotkového náboje? (Ať už můžeme, nebo nemůžeme náboj přenášet nekonečně rychle?)
křivkový integrál (pokud definujeme EM napětí tímhle křivkovým integrálem: ↑ KennyMcCormick:) roven práci vykonané při přesunu jednotkového náboje? (Ať už můžeme, nebo nemůžeme náboj přenášet nekonečně rychle?)
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#93 09. 12. 2018 10:00
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
Ah - ale napětí mezi póly DC zdroje se nemění - je to stále 33V. (Abych si byl 100% jistý, že si rozumíme - práce vykonaná zdrojem při přesunu jednotkového náboje je definice (jedna z definic) EM napětí - ne nezbytně jakéhokoliv napětí. Takže to, že se uvnitř zdroje samotného mění napětí mezi různými dvojicemi bodů (protože tam je i AC zdroj) nemusí nezbytně vadit.)
Tak je to špatná definice. Správná definice je skrze ten integrál všech sil působících na náboj po uzavřené křivce. Z ní plyne ta nekonzervativnost.
A obě definice platit nemohou, když dávají rozdílné výsledky - to bychom měli v systému vnitřní rozpory.
Offline
#94 09. 12. 2018 11:23 — Editoval MichalAld (09. 12. 2018 11:25)
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
Co se týče DC zdroje s proměnným E ve svém vnitřku, kde se náboj přenáší jen po jediné křivce, není v každém okamžiku
křivkový integrál (pokud definujeme EM napětí tímhle křivkovým integrálem: ↑ KennyMcCormick:) roven práci vykonané při přesunu jednotkového náboje? (Ať už můžeme, nebo nemůžeme náboj přenášet nekonečně rychle?)
Je, ale přesunu náboje podél té křivky. Né přesunu náboje mezi póly zdroje.
Napětí mezi póly zdroje nemá na hodnotu integrálu po UZAVŘENÉ křivce žádný vliv. Stejně tak napětí na jakémkoliv jiném pasivním prvku v obvodu.
Jen prostě, za jistých speciálních podmínek, je napětí na svorkách zdroje rovno tomu elektromotorickému. Ale je to jen za jistých podmínek, tím pádem to neplatí vždycky - takže z toho nemůžeme dělat definici.
Offline
#95 10. 12. 2018 05:45
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
Je, ale přesunu náboje podél té křivky. Né přesunu náboje mezi póly zdroje.
Já myslím mezi při přesunu mezi póly zdroje vnitřkem zdroje.
Máme dva zdroje sil: DC zdroj samotný (působí na náboj silou uvnitř zdroje) a póly DC zdroje (působí na náboj elektrickou silou v každém bodě křivky). Celkovou práci získám sečtením prací vykonané oběma silami. Práce vykonaná póly DC zdroje po uzavřené křivce je rovna nule, zbývá tedy jenom práce vykonaná zdrojem mezi póly zdroje. Nebo ne?
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#96 10. 12. 2018 09:11
Re: Různé napětí - stejný proud?
Takže - z práce po uzavřené křivce (obvodu) dostaneme Uem, po křivce venkem zdroje dostaneme U, takže napětí vnitřkem zdroje musí být
Uem = U - Uvnitr, případně Uem = U + Uvnitr, podle toho, jak si zvolíme směry na dílčích cestách.
Když víme, že Uem není v čase konstantní, a svorkové napětí U je v čase konstantní, nutně z toho plyne, že Uvnitr také nemůže být konstantní. Pokud do něj tedy zahrnujeme i ty nekonzervativní síly co tvoří Uem.
Offline
#97 11. 12. 2018 01:48
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
Uem = U + Uvnitr
Ano.
Když víme, že Uem není v čase konstantní
Já tohle ještě nevím. 🙂
Psal jsem:
Máme dva zdroje sil: DC zdroj samotný (působí na náboj silou uvnitř zdroje) a póly DC zdroje (působí na náboj elektrickou silou v každém bodě křivky). Celkovou práci získám sečtením prací vykonané oběma silami. Práce vykonaná póly DC zdroje po uzavřené křivce je rovna nule, zbývá tedy jenom práce vykonaná zdrojem mezi póly zdroje [vnitřkem zdroje]. Nebo ne?
Z toho by plynulo, že práce vykonaná DC zdrojem při přesunu jednotkového náboje mezi póly zdroje vnitřkem zdroje je rovna práci vykonané na jednotkovém náboji při přesunu náboje po uzavřené křivce.
Jestli je to špatně, která část z toho je špatně?
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#98 12. 12. 2018 00:46
Re: Různé napětí - stejný proud?
Ale né....(nemyslím si, že bys neuměl sčítat/odčítat), jen se tvůj mozek nějak brání přijmout ten výsledek).
Máme tedy hezký chemický DC zdroj napětí, který má na svorkách třeba 5 voltů....
Práce kterou by vykonal přenesením jednotkového náboje VNĚ zdroje, od kladného pólu k zápornému bude 5J (jinak by nemohl mít napětí 5V). Tohle napětí označme tedy Uout.
Práci, kterou by vykonal přenesením jednotkového náboje VNITŘKEM zdroje, od kladného pólu k zápornému, zatím neznáme, ale napětí označíme jako Uin.
Elektromotorické napětí zdroje je práce potřebná k přenesení jednotkového náboje z kladného pólu na záporný vnějškem zdroje a pak zase ze záporného na kladný vnitřkem zdroje. Označíme Uemn. Vzhledem k tomu, jak jsme definovali ta předchozí napětí, bude platit
Uemn = Uout - Uin.
Kdybychom si Uin nadefinovali ze záporného pólu na kladný, bylo by tam znaménko plus. Ale na výsledku to nic nemění.
Již dříve jsme se shodli, že u nezatíženého chemického zdroje napětí je svorkové napětí rovné elektromotorickému napětí, tedy Uemn = Uout.
Z toho tedy nutně plyne, že Uin je nulové - a práce vykonaná přenosem náboje vnitřkem zdroje je nulová taky.
Tohle je tedy třeba akceptovat a pochopit, proč to tak je. A není to zas až tak těžké. Uvnitř zdroje působí jednak elektrické síly dané rozdílem potenciálů kladného a záporného pólu - a potom ty neelektrické, nekonzervativní, co nám vlastně vytvářejí to napětí. A u nezatíženého zdroje jsou obě síly v rovnováze. Tudíž napětí je nulové. Nemůže být jiné, to by nám tam protékal proud - vnitřek zdroje je přece vodivý.
Ve skutečnosti bychom k tomu měli přistupovat naopak - z toho, že vnitřkem zdroje neprotéká proud plyne, že síly jsou v rovnováze, a napětí nulové - a z toho plyne, že svorkové napětí zdroje naprázdno je rovné tomu elektromotorickému.
Offline
#99 12. 12. 2018 03:21
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
Máme tedy hezký chemický DC zdroj napětí, který má na svorkách třeba 5 voltů....
Práce kterou by vykonal přenesením jednotkového náboje VNĚ zdroje, od kladného pólu k zápornému bude 5J (jinak by nemohl mít napětí 5V). Tohle napětí označme tedy Uout.
Práci, kterou by vykonal přenesením jednotkového náboje VNITŘKEM zdroje, od kladného pólu k zápornému, zatím neznáme, ale napětí označíme jako Uin.
Elektromotorické napětí zdroje je práce potřebná k přenesení jednotkového náboje z kladného pólu na záporný vnějškem zdroje a pak zase ze záporného na kladný vnitřkem zdroje. Označíme Uemn. Vzhledem k tomu, jak jsme definovali ta předchozí napětí, bude platit
Uemn = Uout - Uin.
Kdybychom si Uin nadefinovali ze záporného pólu na kladný, bylo by tam znaménko plus. Ale na výsledku to nic nemění.
Již dříve jsme se shodli, že u nezatíženého chemického zdroje napětí je svorkové napětí rovné elektromotorickému napětí, tedy Uemn = Uout.
Z toho tedy nutně plyne, že Uin je nulové - a práce vykonaná přenosem náboje vnitřkem zdroje je nulová taky.
To je všechno pravda, ale to není v rozporu s tím, co jsem napsal já. 🙂
Práce vykonaná při přesunu jednotkového náboje vnitřkem DC zdroje je sice nulová, ale to je důsledkem toho, že póly DC zdroje vykonaly práci  a DC zdroj samotný vykonal práci
a DC zdroj samotný vykonal práci  .
.
Celková vykonaná práce na jednotkovém náboji při přesunu náboje vnitřkem DC zdroje je tedy  .
.
Takže to neprotiřečí tomu, co jsem napsal.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#100 12. 12. 2018 08:42
Re: Různé napětí - stejný proud?
No jo, až na ten pojem "práce vykonaná DC zdrojem", který víš přesně jen ty sám, co znamená.
A já už teda ani nevím, co vlastně řešíme.
Jeden čas to bylo o tom, když ten zdroj nebude DC zdroj, ale AC zdroj, a abude mít v sérii diodu a za ní kondenzátor, jestli je jeho elektromotorické napětí stejnosměrné nebo střídavá - no a pak je jasné, že EMN zůstane střídavé vždycky, a o zbytek se postará to "napětí pocházející od pólů" a napětí na diodě.
U DC zdroje vlatně nevím, k čemu se chceme dopacovat.
Ještě mám takový pocit, že se snažíš nějak zařídit definici EMN jen z práce uvnitř zdroje, aby ses vyhnoul tomu integrálu po uzavřené smyčce - ale to bude těžké, protože ty detaily polí uvnitř zdroje prostě neznáme. Zatímco uzavřené smyčce je znát tak úplně nepotřebujeme. Protože uzavřená smyčka nám konzervativní elektrická (a třeba i neelektrická) pole vynuluje automaticky.
Offline
