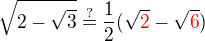Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 12. 2018 21:45
Rovnost komplexních čísel
Zdravím,
Prosím o pomoc s tímto příkladem : Mám zjistit, jestli se čísla rovnají (mělo by vyjít, že ano) 
Někde se našel postup, kde se u Z1 první roznásobí závorky a zjednoduší odmocnina nad 3. Potud bych to zvládla. Ale další krok je dát to celé pod velkou odmocninu, pod kterou tedy je:
((2+6)/4) + (2+odmocnina3)
to se následně upraví do konečného výsledku odmocnina(4+odmocnina 3). Obdobně i se Z2.
Co nechápu je ale jak se mezi ty 2 členy, původně reálnou a imaginární část, dostalo +. i^2 = -1, proto bych čekala že se u 2, odmocnina3 změní znaménka. Nedává mi ani smysl, že původně je to + a -, a po vynásobení stejným členem je zničehonic znaménko stejné....
Snažila jsem se na to přijít s pomocí internetu. Paradoxně, když jsem Z1=Z2 napsala do Mathway, odpovědělo mi to že se ta čísla nerovnají....
Když jsem to zkoušela spočítat sama, s tím že i^2 = -1 a tím tedy pak roznásobím to, co k i patřilo, vyšlo mi z1=odmocnina 3 a Z2=odmocnina(1+odmocnina 3). To se též nerovná.
Tak vůbec nevím, co s tím....
"Když ji miluješ, je pořád co řešit..."
Offline
- (téma jako vyřešené označil(a) Kate X)

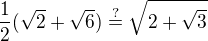 a
a