Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 12. 2018 22:03
loďka, proud
Ahojte ,
Mám seminární práci na fyziku a nejsem si jistá jestli to mám dobře . Najde se tu někdo kdo by mi napsal správný postup? Zadání : Přes řeku širokou 120m, jejíž proud má rychlost 2 m/s, pluje loďka vlastní rychlosti 3 m/s kolmo ke břehům. 1.vypoctete celkovou rychlost loďky
2. Vypoctete čas potřebný k cestě z jednoho břehu na druhy břeh
3. Vypoctete dráhu, kterou loďka urazí při cestě z jednoho břehu na druhy břeh .
Vim ze to je primitivní ale chtěla bych si někde ověřit jestli to mám správně . Dekuju za odpovědi )
Offline
#4 08. 12. 2018 08:59
Re: loďka, proud
Vidím tady problémy ve způsobu zápisu i ve způsobu výpočtu.
Do vzorců je třeba dosazovat hodnoty i s jednotkami. Když se za fyzikální veličiny, které mají jednotky, dosazují jen čísla bez jednotek, učitel to může hodnotit negativně.
nesprávně po stránce zápisu: v = 2 + 3 = 5 m/s, t = 120/5 = 24 s
správně (ale jen po stránce zápisu):  nebo
nebo 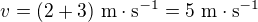 ,
, 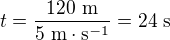
Vlastní rychlost loďky má směr kolmý ke břehům a rychlost proudu má směr rovnoběžný s břehy, takže pro výpočet celkové rychlosti loďky skládáme dvě na sebe kolmé rychlosti, čili počítáme podle Pythagorovy věty, jako když počítáme přeponu pravoúhlého trojúhelníku z odvěsen, tedy nemůžeme je jednoduše sečíst.
Pro výpočet doby plavby použijeme jen vlastní rychlost loďky (v příčném směru, kolmou ke břehům). Rychlejší proud v podélném směru neumožní rychlejší překonání řeky v příčném směru.
Z celkové rychlosti loďky (složené z těch dvou složek rychlosti) a doby plavby vypočítáme ujetou vzdálenost od místa vyplutí k místu doplutí.
Offline
#6 08. 12. 2018 11:17
Re: loďka, proud
↑ Naymar:
Není to tak trošku divné?
Řekněme, že jsem plavec v řece a chci kolmo doplavat na druhý břeh.
Z toho co jste napsali mi přijde, že čím rychlejší je proud, tím rychleji tam budu.
To je vážně divné.
Nicméně pokud se podíváš do sbírky z fyziky od Lepila, tak bz to tam mohlo být.
Jinak existují řešené sbírky od Bartošky.
Offline
#7 08. 12. 2018 13:16
Re: loďka, proud
↑ Pomeranc:
Ja jsem to totiž špatně pochopila, mylslela jsem že loďka pluje po proudu a ne z jednoho na druhy břeh . Dobře dekuju)
Offline
#10 09. 12. 2018 12:22
#11 09. 12. 2018 13:14 — Editoval Jj (09. 12. 2018 13:19)
Re: loďka, proud
↑ Naymar:
Zdravím.
Ano, celková rychlost podle náčrtku ↑ Pomeranc: je v = 2.24 m/s. Jen bych řekl, že ve vzorečku tady ↑ Naymar: je překlep, že má být  .
.
Pokud se tedy nemýlím.
Offline


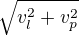


 ,
,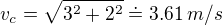 ,
, ,
,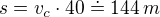 .
.