Matematické Fórum

vonSternberk · 24. 05. 2009 20:46

můžete někdo napovědět s rovnicí:
$3(logx+1)=logx-1$
...já počítal dalej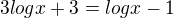
$3logx+3=logx-1$
$2logx+4$
$logx+2$
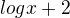
..a co dalej?

gadgetka · 24. 05. 2009 20:55

$\log x=-2\nl10^{-2}=x\nl0,01=x$

vonSternberk · 26. 05. 2009 18:17

můžete mi někdo poradit s tímto příkladem?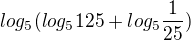
$log_5(log_5125+log_5\frac{1}{25})$
můžu to počítat takto?
$0(125+\frac{1}{25})$
$0$

Alivendes · 26. 05. 2009 18:30

myslím,že pro většinu z nás je mnohem lepší to skenovat než psát...žijem v moderní době :D

vonSternberk · 26. 05. 2009 18:55

↑ Alivendes:
?

gadgetka · 26. 05. 2009 19:06

$\log_5(\log_5 125+\log_5 {\frac{1}{25}})=\log_5 (\log_5 125\cdot \frac{1}{25})=\log_5 (\log_5 5)=\log_5 1=0$

vonSternberk · 26. 05. 2009 19:14

tak toto nechapu:
1) ve druhém kroku jaktoze to muzu nasobit snad potrebuju mit stejny zaklad
2) ve tretim kroku nechapu, kde jsem vzal tu jedničku

ttopi · 26. 05. 2009 19:15

1) Stejný základ máš - 5.
2) 5 na kolikátou je 5? Na prvou.

Zřejmě máš trochu zmatek v definici logaritmu, mrkni se na to ještě.

O.o · 26. 05. 2009 19:18

↑ vonSternberk:

Add 1)
Pokud jsi nějak záhadně nepřečaroval zadání, tak základy stejné jsou, násobit to tedy jde (všude je základem číslo pět).

Add 2)
Bojím se to napsat, protože to nosí poslední dobou méně užitku, ale zkus se rovzpomenout na toto:

$\log_a(b)=c \ \Leftrightarrow \ a^c=b$

vonSternberk · 26. 05. 2009 19:22

Pokud tedy mám stejné základy proč je nemuzu odstranit hned na zacatku rovnice a napsat $0(125+\frac{1}{25})$ ??

gadgetka · 26. 05. 2009 19:28

protože to, cos napsal je blbost, mrkni na pravidla logaritmování :)

vonSternberk · 26. 05. 2009 19:32

jj už rozumím...musím sčítat nebo odčítat abych mohl použít pravidlo pro stejný základ

O.o · 26. 05. 2009 19:36

↑ vonSternberk:

Jednoduché, zaprvé, žádná nula tam není, ty bys chtěl mít výsledek samé nuly, či co.

Po zaprvé má prý následovat zadruhé, tedy zadruhé: nemáš rovnici, máš jen výraz, ten můžeš upravovat, ale nic víc (ne že si tam z čista jasně vymyslíš rovná se nule, protože pak by šlo o něco jiného a v krajních případech bys mohl dostat příklad, kde by něco takového udělat nešlo!).

Za třetí, co jsi napsal (nekoukám se teď na nulu, opravdu ;-)) je celé špatně. ttopi ti poradil ať se podíváš na definici logaritmu, já ti ji napsal, tak se na to mrkni a pořádně si to vryj do hlavy, ve tři ráno tě probudí ledovou sprchou a ty budeš vědět, co s takovýmhle lgoaritmem můžeš dělat, oki? Budeš to potřebovat!

To, co se snažíš naznačit by šlo udělat v tomto případě:

$\log_5(\log_5(A)+\log_5(B))=\log_5(C) \ \Leftrightarrow \ \log_5(A)+\log_5(B)=C$

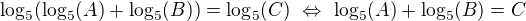
Nejlepší je, když to popíši slovně, tedy: výraz na levé straně se rovná výrazu na pravé straně právě tehdy, když se rovnají jejich argumenty (pro tebe doplním ještě: jen tehdy !, pokud budu mít na obou stranách rovnice samostatně logaritmy o stejném základu, není to železné pravidlo, můžeš porovnávat třeba koeficienty u polynomů, atp.., ale u těch logaritmů se to tak na střední dělá (kdy by to třeba nešlo viz. níže).

Kdy ti profesorka utrhne prsty a hlavu otočí o třistašedesát stupňů?
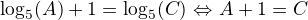$\log_5(A)+1=\log_5(C) \ \cancel{\Leftrightarrow} \ A+1=C$ - jak tohle uděláš, tak tě někdo zadupe, pamatovat si to, oki? Nejprve to chce udělat úpravy, abys "osamostatnil" logaritmy, rozumíme?

Správně by bylo:
$\log_5(A)+1=\log_5(C) \nl \log_5(A \cdot 5)=\log_5(C) \ \Leftrightarrow \ 5A=C$

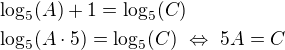
Heh snad jsem se někde nepřepsal =).

marnes · 26. 05. 2009 19:36

↑ vonSternberk:Hlavně musíš upravovat tak, aby jsi měl na obou stanách jen jeden logaritmus ( talíře ) a pak můžeš porovnávat to, co je na těch talířích. V zadání máš talíř, na tom tácek a ještě misku:-)

O.o · 26. 05. 2009 19:38 — Editoval O.o (26. 05. 2009 19:38)

↑ marnes:

OT:

=oD po misce by bylo co? Já už bych tam rád viděl třeba i steak (medium) s hranolkami, ale jak pak z těch logaritmů ty pochoutky dostat, to by byl zázrak ;-).

PS: Děkuji za pobavení, večer se hend lépe usíná..

marnes · 26. 05. 2009 19:40

↑ O.o:A pak že matika není zábavná:-) Doufám, že matici mě pochopili:-)

vonSternberk · 26. 05. 2009 19:41

muzu se jeste tedy zeptat mám-li toto:
$log_{0,5}(log_39)$
řeším:
$log_{0,5}(log_33^3)$
$log_{0,5}(log1^3)$
$log_{0,5}0$
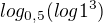
vysledek 0, ale to je bohuzel spatne:(

ttopi · 26. 05. 2009 19:44

3 na kolikátou je 9? na druhou, proto je hodnota závorky 2. Pak se ptáš, na kolikátou umocním 0,5 abych dostal 2?

gadgetka · 26. 05. 2009 20:00

$(\frac{1}{2})^x=2$
Kolik je x? :)

gadgetka · 26. 05. 2009 20:02

$\log_{0,5}(\log_3 9)=\log_{\frac{1}{2}}(2)=-1$

vonSternberk · 26. 05. 2009 20:04

-1:)

vonSternberk · 26. 05. 2009 20:11

a muzete jeste tento:
$log_2\frac{0.5^2}{\sqrt{8}}$

marnes · 26. 05. 2009 20:52

↑ vonSternberk:Uprav nejdříve zlomek
0,5^2=[1/2]^2=2^-2
odm8=odm[2^3]=2^[3/2]

cely zlomek 2^[-2-3/2]=2^[-7/2]
vysledek logaritmu -7/2

M@rvin · 26. 05. 2009 20:55

$log_2\frac{(\frac{1}{2})^2}{\sqrt{8}}\nl\frac{(\frac{1}{2})^2}{\sqrt{8}}=\frac{2^{-2}}{8^\frac{1}{2}}=\frac{2^{-2}}{2^\frac{3}{2}}=2^{-\frac{7}{2}}\nllog_22^{-\frac{7}{2}}=-\frac{7}{2}$

gadgetka · 27. 05. 2009 00:59

jen jsem si dovolila upravit tex :)

$\log_2\frac{(\frac{1}{2})^2}{\sqrt{8}}\nl\frac{(\frac{1}{2})^2}{\sqrt{8}}=\frac{2^{-2}}{8^{\frac{1}{2}}}=\frac{2^{-2}}{2^{\frac{3}{2}}}=2^{-\frac{7}{2}}\nl\log_22^{-{\frac{7}{2}}}=-\frac{7}{2}$

Matematické Fórum

#26 24. 05. 2009 20:46

Re: Logaritmická rovnice

#27 24. 05. 2009 20:55

Re: Logaritmická rovnice

#28 26. 05. 2009 18:17

Re: Logaritmická rovnice

#29 26. 05. 2009 18:30

Re: Logaritmická rovnice

#30 26. 05. 2009 18:55

Re: Logaritmická rovnice

#31 26. 05. 2009 19:06

Re: Logaritmická rovnice

#32 26. 05. 2009 19:14

Re: Logaritmická rovnice

#33 26. 05. 2009 19:15

Re: Logaritmická rovnice

#34 26. 05. 2009 19:18

Re: Logaritmická rovnice

#35 26. 05. 2009 19:22

Re: Logaritmická rovnice

#36 26. 05. 2009 19:28

Re: Logaritmická rovnice

#37 26. 05. 2009 19:32

Re: Logaritmická rovnice

#38 26. 05. 2009 19:36

Re: Logaritmická rovnice

#39 26. 05. 2009 19:36

Re: Logaritmická rovnice

#40 26. 05. 2009 19:38 — Editoval O.o (26. 05. 2009 19:38)

Re: Logaritmická rovnice

#41 26. 05. 2009 19:40

Re: Logaritmická rovnice

#42 26. 05. 2009 19:41

Re: Logaritmická rovnice

#43 26. 05. 2009 19:44

Re: Logaritmická rovnice

#44 26. 05. 2009 20:00

Re: Logaritmická rovnice

#45 26. 05. 2009 20:02

Re: Logaritmická rovnice

#46 26. 05. 2009 20:04

Re: Logaritmická rovnice

#47 26. 05. 2009 20:11

Re: Logaritmická rovnice

#48 26. 05. 2009 20:52

Re: Logaritmická rovnice

#49 26. 05. 2009 20:55

Re: Logaritmická rovnice

#50 27. 05. 2009 00:59

Re: Logaritmická rovnice

Zápatí