Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Limitny maraton
#201 16. 12. 2018 12:13 — Editoval vanok (16. 12. 2018 12:15)
Re: Limitny maraton
Pozdravujem ↑↑ krakonoš: ( ja vzdy pozdravim, aj ked nietori tu to nedokazu).
Nie to nie je dobra odpoved.
Tak dam prvy hint.
Ako prve mozte prestudovat 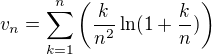
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#202 16. 12. 2018 13:03
Re: Limitny maraton
Ahoj ↑↑ vanok:↑↑ krakonoš:.
1/3 je hodne hruby horni odhad:
Pro clen 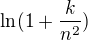 je tento odhad tesny (protoze druhy clen Taylorova rozvoje
je tento odhad tesny (protoze druhy clen Taylorova rozvoje 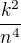 je zanedbatelny), ale pro clen
je zanedbatelny), ale pro clen  horni odhad nestaci.
horni odhad nestaci.
Proto staci opravdu zkoumat 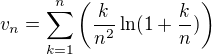 .
.
To je ale site na definici Riemannova integralu:![kopírovat do textarea $\lim_{n\to\infty}v_n=\int_0^1x\ln(1+x)\,\mathrm{d}x=[\tfrac12x^2\ln(1+x)]_0^1-\tfrac12\int_0^1\frac{x^2}{1+x}\,\mathrm{d}x\\
=\tfrac12\ln 2-\tfrac12\int_0^1(x-1)\,\mathrm{d}x-\tfrac12\int_0^1\frac1{x+1}\,\mathrm{d}x\\
=\frac14$](/mathtex/f1/f1f0833f2623b23fa576687c7579016a.gif) .
.
Oduvodneni  :
:
Z nerovnosti  ,
, 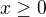 , zrejme plyne
, zrejme plyne 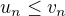 . Na druhou stranu vyuzijeme nerovnost
. Na druhou stranu vyuzijeme nerovnost 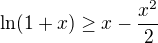 , ktera plyne napr. z vysetreni prubehu funkce
, ktera plyne napr. z vysetreni prubehu funkce 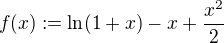 na
na 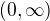 . Z teto nerovnosti dostaneme
. Z teto nerovnosti dostaneme ,
,
kde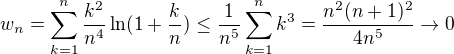 ,
, 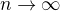 .
.
Pouzitim vety od 2 policajtech dostavame, co jsme chteli.
Offline
#203 16. 12. 2018 13:41
Re: Limitny maraton
Ahoj ↑ Bati:,
Ano to je dobra metoda a pochopitelne da aj cakanu dobru odpoved.
Len poznamenam, ze ani netreba pouzit Taylorov rozvoj: staci ukazat, ze pre kladne realne x, mame 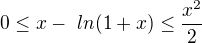 ( na to staci vysetrit vhodne funkcie, a tak takuto otazku mozme dat studentom, ktori poznaju Riemannovu sumu a vediet vysetrovat klasicke funkcie, ako si naznacil a pouzil; tiez mame trochu lepsiu nerovnost
( na to staci vysetrit vhodne funkcie, a tak takuto otazku mozme dat studentom, ktori poznaju Riemannovu sumu a vediet vysetrovat klasicke funkcie, ako si naznacil a pouzil; tiez mame trochu lepsiu nerovnost 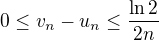 ...ktoru lahko ukazes, co da ze limita rozdielu je nulova a tak
...ktoru lahko ukazes, co da ze limita rozdielu je nulova a tak 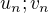 maju rovnake limity).
maju rovnake limity).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#204 16. 12. 2018 15:44
#205 16. 12. 2018 18:05
Re: Limitny maraton
Cau ↑ Bati:,
Rozvoj okolo 0, nam da okamzite nulovu limitu.
Ale mozno cakas na ine riesenie? Ake?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#206 16. 12. 2018 18:24
Re: Limitny maraton
↑ vanok:
Myslis nulovou limitu jmenovatele? Protoze pri prevedeni na spolecneho jmenovatele to je typu -360-360-720/0.Takze vysledna by mala byt nekonecno.Jestli jsem se nespletla v upravach.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#207 16. 12. 2018 18:42 — Editoval vanok (16. 12. 2018 18:43)
Re: Limitny maraton
Cau ↑ krakonoš:
Ked urobis rozvoj najed nulovu limitu. Staci to robit pre kazdy zlomok v zatvorke a uvidis, ze prve dva cleny sa potom anuluju. ( Mozes ist napr. do radu O(x^7), co staci).
Mocnina pred zatvorkou celeho vyrazu, nic nezmeni na vysledku. (Vsak 1/11<6).
No mozno kolega myslel na nejaku inu metodu. Iste na o tom napise. 😀
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#208 16. 12. 2018 20:08
#209 16. 12. 2018 20:23
Re: Limitny maraton
↑ Bati:,
Ano, mas pravdu, no na stastie je ta mocnina mensia ako 6.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#210 16. 12. 2018 20:44 — Editoval krakonoš (16. 12. 2018 21:02)
Re: Limitny maraton
Ja si nemuzu pomoct,ale vyjadrim-li hyperbolicky cosinus pomoci exponenciely a prevedu-li vse na spolecny zlomek,tak je to opravdu nekonecno t.j. limita zavorky.Navic vzhledem k druhe odmocnine ve jmenovateli ma spis smysl limita zprava k nule.Takze to beru jako chybu zaznamu ,ze tam chybi ten krizek.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#211 16. 12. 2018 22:57
Re: Limitny maraton
Pozdravujem ↑ krakonoš:,
To mas pravdu, to + v riguroznom pisani chyba. No vsak ten komentar, moze pytat skusajuci, aby overil, ci student isiel dostatocne do hlbky co sa tyka cvicenia.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#212 16. 12. 2018 23:47
Re: Limitny maraton
↑ vanok:
zalezi na tom jestli to Beti vymyslela sama a na krizek zapomnela,a nebo je to opsano z literatury a je to chytak(je tam ta 11mocnina licha).V prvni chvili jsem si to taky neuvedomila.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#213 17. 12. 2018 05:07
Re: Limitny maraton
Cau ↑ krakonoš:,
Takto mas material ako vymysliet sama cvicenia pre inych. Dobry pocit, ze.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#214 17. 12. 2018 05:27
Re: Limitny maraton
problem (50)
Najdite 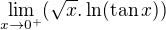 .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#215 17. 12. 2018 08:50
Re: Limitny maraton
↑ vanok:
Využijeme-li,ze tan(x) se na okolí nuly chová jako x a nasledně rozvedeme ln(x) na okolí bodu 1 v Taylorovu řadu,dostaneme,že limita je rovna nule.
Nebo můžeme limitu pro x jdouci k nule zprava převést na limitu typu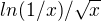 ,kde x konverguje do nekonecna a použít LHospitalovo pravidlo.
,kde x konverguje do nekonecna a použít LHospitalovo pravidlo.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#216 17. 12. 2018 09:43 — Editoval vanok (17. 12. 2018 09:44)
Re: Limitny maraton
Dobre rano ↑ krakonoš: ,
Co je zaujimave, tento problem sa da vyriesit o mnoho jednoduchsie.
Hint. Vyuzite, ze  (pre kladne dostatocne male
(pre kladne dostatocne male  ). Cakame dokaz, kde vsetko dokladne zvodnite.
). Cakame dokaz, kde vsetko dokladne zvodnite.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#217 17. 12. 2018 11:02
Re: Limitny maraton
↑ krakonoš:
Limitu jsem si vymyslel. Limita zavorky je samozrejme 0, ale jde o to ukazat, ze ani ta zaporna mocnina pred tim to nezkazi. Odmocninu zaporneho cisla jsem prehledl, ale pokud by to byla komplexni odmocnina, je to ok.
Offline
#219 17. 12. 2018 16:41
#220 18. 12. 2018 08:56
Re: Limitny maraton
Ahoj ↑ krakonoš:,
Taka myslienka, ak dobre rozumiem sa vola ekvivalencia funkcii.
Tak prva etapa je to najprv dokazat a potom pokracovat.
O tom som tu uz vela pisal, ( I ked bez vela uspechu, ale to je tiez velmi ucinna metoda, no zda sa, ze vobec neuci na sk, cz... skoda)
Ked budem mat cas pridam jedno cele riesenie problemu (50).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#221 18. 12. 2018 10:08
Re: Limitny maraton
Ahoj ↑ Pavel:,
Problem(51).
Myslim si, ze staci vysetrit v okoli nuly  a aj
a aj 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#222 18. 12. 2018 10:59
Re: Limitny maraton
↑ Pavel:
Ahoj
Ja si myslim,ze se to prevede na spolecny zlomek,rozdil logaritmu v citateli se vyjadri jako logaritmus podilu.Dostaneme jeden logaritmus v citateli a soucin dvou logaritmu ve jmenovateli.Kazdy argument logaritmu jde k jedne,takze muzeme vyuzit,ze
ln(argument) se chova na okoli 1 stejne jako (argument -1).Az se dostaneme k vyrazu ( cos(sinx)-cosx)/(cosx.(cosx-1).(cos(sinx)-1)),kde x jde k nule.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#223 18. 12. 2018 11:21
#224 18. 12. 2018 13:40 — Editoval Pavel (18. 12. 2018 13:44)
Re: Limitny maraton
↑ vanok:
Proč právě  ?
?
↑ krakonoš:
To by šlo. Co dál?
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#225 18. 12. 2018 15:12
Re: Limitny maraton
Cau ↑ Pavel:,
Pretoze potom tie ekvivalenty su 1/3 a-1/3.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Limitny maraton

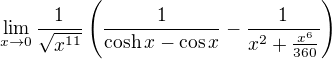 .
.![kopírovat do textarea $\frac{1}{\sqrt[11]x}$](/mathtex/16/1653beea6347fa89f1547277f595ec4b.gif) , ale
, ale 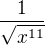 , ale jinak mas pravdu. Pro uplnost napisu podrobne reseni:
, ale jinak mas pravdu. Pro uplnost napisu podrobne reseni: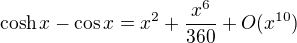 , takze s vyuzitim vzorce pro soucet geometricke rady dostaneme
, takze s vyuzitim vzorce pro soucet geometricke rady dostaneme . Proto
. Proto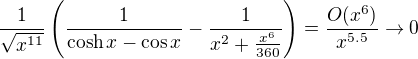 ,
,  .
.
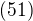 Finding
Finding 