Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Jednoduché nezáporné integrovatelné funkce (TOTO TÉMA JE VYŘEŠENÉ)
#2 23. 12. 2018 15:54 — Editoval jardofpr (26. 12. 2018 13:44)
Re: Jednoduché nezáporné integrovatelné funkce
ahoj ↑ Flaky:
mne to príde že si len zapísal tvrdenie ktoré sa snažíš dokázať, pričom mi nie je úplne jasné čo myslíš zápisom 
mimochodom JNI znamená len  a
a  ?
?
potom môžeš použiť napr. 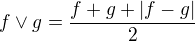 ,
,  (ak je
(ak je  JNI tak aj
JNI tak aj 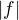 je JNI)
je JNI)
alebo použiť 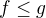 skoro všade, tak
skoro všade, tak 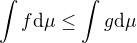

prípadne rozpis oboch funkcií na ich súčty cez charakteristické funkcie
Offline
#3 26. 12. 2018 10:21 — Editoval Flaky (26. 12. 2018 10:23)
Re: Jednoduché nezáporné integrovatelné funkce
Mno, kdybych si takto rozepsal danou funkci, pak tedy dostanu jednu polovinu ze součtu integrálů z f ,g a abs(f-g), o kterých lze říci , že jsou všechny menší, než nekonečno z integrovatelnosti obou funkcí f a g
a druhý případ se bude lišit akorát znaménkem před posledním sčítancem.
The only way to learn mathematics is to do mathematics.
- Paul Halmos -
Offline
#4 26. 12. 2018 13:48
Re: Jednoduché nezáporné integrovatelné funkce
↑ Flaky:
skoro tak, tú absolútnu hodnotu ešte rozbiť cez trojuholníkovú nerovnosť aby si to mal úplne čisté
ale reálne aj tak budeš potom potrebovať výsledok označený hviezdičkou v príspevku vyššie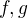 sú nezáporné okrem iného tak by mohlo byť jednoduchšie
sú nezáporné okrem iného tak by mohlo byť jednoduchšie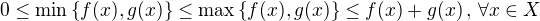
Offline
#5 26. 12. 2018 15:46
Re: Jednoduché nezáporné integrovatelné funkce
↑ jardofpr:
No, je to rozdil dvou jednoduchych meritelnych funkci, ktery je jednoducha meritelna funkce a meritelna funkce je integrovatelna prave tehdy, kdyz je jeji abs. Hodnota integrovatelna
The only way to learn mathematics is to do mathematics.
- Paul Halmos -
Offline
#7 26. 12. 2018 19:12
Re: Jednoduché nezáporné integrovatelné funkce
Ano, to jsem měl na mysli. Dostanu tedy ve výsledku jednu polovinu ze součtu integrálů, kde na poslední z nich aplikuji troj. nerovnost, čímž docílím toho, že bude ve všech vystupovat pouze funkce f či g a tedy budou všechny sčítance menší, než nekonečno z předpokladu
The only way to learn mathematics is to do mathematics.
- Paul Halmos -
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Jednoduché nezáporné integrovatelné funkce (TOTO TÉMA JE VYŘEŠENÉ)



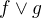 potrebuješ
potrebuješ  a máš k dispozícii
a máš k dispozícii  , preto to rozbitie absolútnej hodnoty
, preto to rozbitie absolútnej hodnoty