Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 12. 2018 10:35
JNI fce.
Zdravím,
mám tu ještě jeden příklad na stejné téma, a to sice, zda se dá něco říci o integrovatelnosti nezáporných jednoduchých měřitelných funkcí f a g, pakliže je funkce 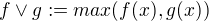 integrovatelná.
integrovatelná.
Vím tedy ze zadání, že integrál dle míry 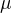 z této funkce
z této funkce 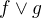 je menší, než
je menší, než  .
.
Proto mě napadlo, zda by nešlo vzít nějakou funkci, která bude menší rovna funkci 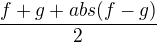 (vyjádření
(vyjádření 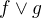 ), a poté využít toho, že platí- li nerovnost pro funkční hodnoty f(x), g(x), pak platí i pro integrály podle míry z těchto funkcí.
), a poté využít toho, že platí- li nerovnost pro funkční hodnoty f(x), g(x), pak platí i pro integrály podle míry z těchto funkcí.
The only way to learn mathematics is to do mathematics.
- Paul Halmos -
Offline
- (téma jako vyřešené označil(a) Flaky)
#3 27. 12. 2018 11:26
Re: JNI fce.
↑ Flaky:
Ahoj.
Z Tvých předpokladů plyne, že funkce  je nezáporná, měřitelná a má integrovatelnou
je nezáporná, měřitelná a má integrovatelnou
majorantu ( konkretně funkci 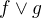 ). Z toho plyne, že
). Z toho plyne, že  je integrovatelná. Příslušnou
je integrovatelná. Příslušnou
větu s důkazem jistě nebude těžké najít v Jarníkově I2 .
Offline
#4 27. 12. 2018 16:53
Re: JNI fce.
no já jsem si vzal polovinu z f(x), aby bylo jasné, že je menší rovna (f v g) , pak pouze dostanu ze integrál z f je mensi roven, nez 2*integral z (fvg), který je mensi, nez nekonecno
The only way to learn mathematics is to do mathematics.
- Paul Halmos -
Offline
#5 27. 12. 2018 20:50
Re: JNI fce.
↑ Flaky:
ako píšeš je to tiež ok, čo som sa snažil povedať je len že ti netreba ten rozpis funkcie max
keďže platí priamo nerovnosť ktorú som napísal vyššie pre tvoje funkcie z predpokladov
ahoj ↑ Rumburak:
áno na tento výsledok som sa odvolával v predošlej téme ktorú kolega otvoril,
verím že už používa na štúdium iný ako Jarníkov materiál
Offline
#6 28. 12. 2018 10:17 — Editoval Flaky (28. 12. 2018 10:20)
Re: JNI fce.
↑ jardofpr:
Ano, to jistě také jde, já akorát pouzil rozpis, neb jsem ho pouzival i v oné minulé úloze, a tak me napadl jeste drive, nez triviální nahlédnutí. Kazdopádně děkuji za ověření.
The only way to learn mathematics is to do mathematics.
- Paul Halmos -
Offline

 )
)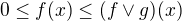 a to isté pre
a to isté pre