Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#101 29. 12. 2018 02:13 — Editoval KennyMcCormick (29. 12. 2018 02:15)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
přitom třeba samotné Maxwellovy rovnice nejsou správným modelem pro střídavé napětí (střídavá pole)
Jak to? Neplatí Maxwellovy rovnice v celém klasickém elektromagnetismu? Nebo mluvíš o případě, kdy klasický elektromagnetismus už neplatí?
↑↑ MichalAld:
Jeden čas to bylo o tom, když ten zdroj nebude DC zdroj, ale AC zdroj, a abude mít v sérii diodu a za ní kondenzátor, jestli je jeho elektromotorické napětí stejnosměrné nebo střídavá
To je taky DC zdroj, konkrétně DC zdroj, jehož jednou komponentou je AC zdroj. 🙂
No jo, až na ten pojem "práce vykonaná DC zdrojem", který víš přesně jen ty sám, co znamená.
Máme dva fyzikální systémy: póly DC zdroje a DC zdroj jako takový. Rozdíl mezi nimi je ten, že "póly DC zdroje" jsou kladný a záporný pól DC zdroje vytvářející elektrostatické (konzervativní) pole, zatímco "DC zdroj" je ten zbytek, který vytváří (nekonzervativní) pole elektromotorických sil.
Tj. protože jsem celý systém rozdělil na subsystémy "póly DC zdroje" a "DC zdroj" (jejichž sjednocením je celý systém), "práce vykonaná DC zdrojem" není totéž jako "vykonaná práce".
(Teď opakuju, co jsem napsal předtím.)
Teď se (snad) shodneme na tom, že v případě DC zdroje je práce vykonaná DC zdrojem při přesunu jednotkového náboje vnitřkem zdroje rovna celkové práci vykonané po celé uzavřené křivce.
(Tohle ale nebude důležité pro to, co píšu dál.)
A já už teda ani nevím, co vlastně řešíme.
Vztah mezi jednotlivými definicemi (čistě proto, abych tomu já osobně rozuměl).
Předtím jsme se shodli, že pro DC zdroje platí, že definice EMN coby "celková práce vykonaná při přesunu jednotkového náboje po uzavřené křivce" je rovna svorkovému napětí ideálního zdroje. Taky jsme se shodli, že EMN definované přes křivkový integrál je ekvivalentní definici EMN coby "celková práce vykonaná při přesunu jednotkového náboje po uzavřené křivce".
Z toho plyne, že pro DC zdroje platí, že EMN definované přes křivkový integrál je rovno svorkovému napětí ideálního zdroje.
Takže pro DC zdroje máme 2 definice EMN:
1. Celková práce vykonaná při přesunu jednotkového náboje po uzavřené křivce
2. Definice přes křivkový integrál
A pro obě tyto definice platí, že svorkové napětí ideálního DC zdroje je rovno EMN tohoto zdroje.
Pro AC zdroje mě napadají 2 možné definice EMN:
1. Záporně vzatá změna indukčního toku za čas: 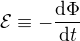
2. Přes křivkový integrál (stejně jako v případě DC zdrojů)
Pro definici 1 neplatí nezbytně, že svorkové napětí ideálního AC zdroje je rovno EMN (např. v případě elektronických AC zdrojů).
Pro definici 2 platí vždy, že svorkové napětí ideálního AC zdroje je rovno EMN. (Protože máme zákon zachování energie.)
(Oprav mě, jestli jsem se někde spletl.)
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#102 29. 12. 2018 13:27
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
Takže pro DC zdroje máme 2 definice EMN:
1. Celková práce vykonaná při přesunu jednotkového náboje po uzavřené křivce
2. Definice přes křivkový integrál
A pro obě tyto definice platí, že svorkové napětí ideálního DC zdroje je rovno EMN tohoto zdroje.
Jenomže ty definice nejsou obecně ekvivalentní - jedna (ta správná) využívá křivovký integrál elektrické intenzitý (nebo ekvivalentní neelektrické intenzity - tj síly vztažené na přenos jednotkového náboje) a ta druhá využívá práci. Ale práce není jen el. intenzita, je to taky proud.
A to je jádro problému - ty dvě definice budou ekvivalentní pouze za předpokladu, že dráha proudu bude identická s tou smyčkou, podél které počítáme integrál E.
Jenže to je splněno jen v nejjednodušších případech. Pokud dráhu proudu rozvětvíme, tak už to pravda nebude. Nejtriviálnější případ co mě napadá je zdroj opatřený odporovým děličem.
A stejné je to u toho AC zdroje, který jsme doplnili usměrňovací diodou a kondenzátorem. Část proudu teče přes ten fitrační kondenzátor a část odebíráme ze svorek zdroje.
A nemá žádný smysl vymýšlet 50 definic EMN, mnohem lepší je mít jen jednu, ale pořádnou (univerzální, co platí vždycky). A další věc je, že by z toho měl být nějaký užitek. Nás obecně nemusí zajímat nějaká "virtuální veličina", my potřebujeme dělat správné předpovědi. Pokud nám v tom ta veličina EMN nijak nepomůže, tak ji nemusíme zavádět vůbec.
Offline
#103 29. 12. 2018 13:33
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
Pro AC zdroje mě napadají 2 možné definice EMN:
1. Záporně vzatá změna indukčního toku za čas:
2. Přes křivkový integrál (stejně jako v případě DC zdrojů)
K definici 1. - nemůžeme obecně vědět, jestli nelze střídavé napětí vyrobit i jinak než el. mag. indukcí.
(lze to udělat třeba také na kondenzátoru s proměnnou kapacitou, nebo rovnou na piezoelektrickém měniči)
KennyMcCormick napsal(a):
Pro definici 1 neplatí nezbytně, že svorkové napětí ideálního AC zdroje je rovno EMN (např. v případě elektronických AC zdrojů).
Pro definici 2 platí vždy, že svorkové napětí ideálního AC zdroje je rovno EMN. (Protože máme zákon zachování energie.)
(Oprav mě, jestli jsem se někde spletl.)
Pro definici 2 to neplatí taky, protože jak už jsem zmiňoval, pokud dráha proudu nebude stejná jako dráha po které počítáme integrál (např. když dráhu proudu rozvětvíme) tak to také platit nebude.
Offline
#104 29. 12. 2018 13:38
Re: Různé napětí - stejný proud?
Mmch, není až tak velký problém si představit zdroj (mám ho zrovna na stole) který má vícero svorek a na každém páru svorek je jiné napětí. A přitom uvnitř zdroje může být jediné zdroj EMN, třeba transformátor s jediným sekundárním vinutím - a všechna ta svorková napětí jsou z něj odvozená.
Definice EMN (ať už bude jakákoliv) musí vycházet z toho, co zdroji zajišťuje ten "trvalý zdroj energie" a na svorkovém napětí to nemusí záviset vůbec. To je jen shoda okolností, že si to za jistých podmínek odpovídá.
Offline
#105 29. 12. 2018 14:08 — Editoval edison (29. 12. 2018 14:20)
Re: Různé napětí - stejný proud?
↑ MichalAld:Navíc to střídavé napětí může být generováno čistě elektronicky (procesor-DAC-zesilovač) a lézt z dalšího páru svorek na zmíněném vícenásobném zdroji. A když se bude jednat o zesilovač s DC vazbou, můžeme dokonce za chodu volit, zda bude na výstupu AC, DC, nebo obojí dohromady:-)
Edit: A jelikož je pravděpodobně více harddisků než aut s alternátorem, můžeme s jistotou tvrdit, že elektronických AC zdrojů je většina.
Edit2: A to jsem nějak zapomněl na zdroje AC signálů. Těch je od dob LVDS sběrnic v počítačích a telefonech hromada.
Offline
#106 30. 12. 2018 10:25 — Editoval KennyMcCormick (30. 12. 2018 10:30)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
A to je jádro problému - ty dvě definice budou ekvivalentní pouze za předpokladu, že dráha proudu bude identická s tou smyčkou, podél které počítáme integrál E. (...) Pro definici 2 to neplatí taky, protože jak už jsem zmiňoval, pokud dráha proudu nebude stejná jako dráha po které počítáme integrál (např. když dráhu proudu rozvětvíme) tak to také platit nebude.
Sorry, na to jsem zapomněl, i když jsme na tom už předtím shodli, tj. co jsem napsal o definici přes křivkový integrál platí jenom pro případy, kde se náboj pohybuje pouze po jedné křivce.
K definici 1. - nemůžeme obecně vědět, jestli nelze střídavé napětí vyrobit i jinak než el. mag. indukcí.
Díky, vím, že to jde i jinak - byla to jako jedna z rovnic (ne definic) v učebnici, ale jestli se to nepoužívá jako definice, tak to vyřadíme.
Takže, abych opravil, co jsem napsal v předchozím příspěvku:
Takže pro DC zdroje máme 2 definice EMN:
1. Celková práce vykonaná při přesunu jednotkového náboje po uzavřené křivce
2. Definice přes křivkový integrál
Pro první definici platí, že svorkové napětí ideálního DC zdroje je rovno EMN tohoto zdroje. Pro druhou definici platí, že svorkové napětí ideálního DC zdroje je rovno EMN tohoto zdroje, pokud se náboj přenáší pouze po jedné křivce.
Pro ideální AC zdroje bych použil stejnou definici přes křivkový integrál jako pro DC zdroje, a v případě náboje putujícího po jediné křivce opět platí, že EMN zdroje je rovno svorkovému napětí.
Teď už se na tom (snad) shodneme.
Co se týče definice přes křivkový integrál, myslím, že ji můžeme zobecnit na více cest tak, aby byla ekvivalentní definici přes práci - jednoduše tak, že budu integrovat přes všechny křivky, kterými náboj prochází. Takže pokud označím  množinu křivek, kterými náboj prochází, pak EMN definované jako
množinu křivek, kterými náboj prochází, pak EMN definované jako![kopírovat do textarea $\mathcal{E}\equiv\int\limits_\Omega\left(\oint\limits_\mathcal{C}[\textbf{E}+\textbf{v}\times\textbf{B}]\d\textbf{l}+\frac1 q\oint\limits_\mathcal{C}(\text{efektivní chemické síly})\d\textbf{l}+\frac1 q\oint\limits_\mathcal{C}(\text{efektivní termální síly})\d\textbf{l}\right)\d\Omega$](/mathtex/89/89be292ecf95bccac012306e4c3da5cd.gif)
by bylo ekvivalentní definici EMN přes práci. Je to tak?
Mmch, není až tak velký problém si představit zdroj (mám ho zrovna na stole) který má vícero svorek
Hm... není to z hlediska teorie více zdrojů v jediném fyzickém umístění?
Pokud je to jediný zdroj, tak máš samozřejmě pravdu, protože jedno číslo (EMN zdroje) nemůže být zároveň rovno více různým číslům (různým napětím na různých svorkách). To je jasné. 🙂
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#107 30. 12. 2018 18:07
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
Mmch, není až tak velký problém si představit zdroj (mám ho zrovna na stole) který má vícero svorek
Hm... není to z hlediska teorie více zdrojů v jediném fyzickém umístění?
Pokud je to jediný zdroj, tak máš samozřejmě pravdu, protože jedno číslo (EMN zdroje) nemůže být zároveň rovno více různým číslům (různým napětím na různých svorkách). To je jasné. 🙂
Z hlediska "teorie" to může být cokoliv, záleží na tom, jakou "teorii" budeme používat.
Ale z hlediska fyziky není těžké si představit zdroj, obsahující jeden olověný akumulátor - což je to jediné, co má nějaké elektromotorické napětí - ze kterého budeme napájet tři lineární stabilizátory (doufám že víš, co to je), každý na jiné napětí.
Offline
#108 30. 12. 2018 18:10
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
Takže, abych opravil, co jsem napsal v předchozím příspěvku:
Takže pro DC zdroje máme 2 definice EMN:
1. Celková práce vykonaná při přesunu jednotkového náboje po uzavřené křivce
2. Definice přes křivkový integrál
Pro první definici platí, že svorkové napětí ideálního DC zdroje je rovno EMN tohoto zdroje. Pro druhou definici platí, že svorkové napětí ideálního DC zdroje je rovno EMN tohoto zdroje, pokud se náboj přenáší pouze po jedné křivce.
Ale né, je to přesně naopak - definice pomocí křivového integrálu je univerzální a definice pomocí práce vyžaduje přenos (veškerého) náboje po jedné křivce.
Pro ideální AC zdroje bych použil stejnou definici přes křivkový integrál jako pro DC zdroje, a v případě náboje putujícího po jediné křivce opět platí, že EMN zdroje je rovno svorkovému napětí.Teď už se na tom (snad) shodneme.
Offline
#109 30. 12. 2018 18:19
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
Co se týče definice přes křivkový integrál, myslím, že ji můžeme zobecnit na více cest tak, aby byla ekvivalentní definici přes práci - jednoduše tak, že budu integrovat přes všechny křivky, kterými náboj prochází.
Tohle vůbec nemusíme dělat - křivkový integrál nám dá buď správnou hodnotu, nebo nulu.
A pokud né - když naše krabička obsahuje více nějakých zdrojů nebo komplikované proměnné pole - no tak o nějakém EMN už asi nemůžeme mluvit vůbec.
Jinak ještě upozorňuji, že tvá představa o "integrování přes více smyček" není asi úplně korektní. Já sám moc nechápu, jak si to představuješ.
Navíc mi uniká proč - při definici EMN přes křivkový integrál nemáme problém s tím, že bychom museli procházet všechny cesty - s tím máme problém jen při té definici skrze práci.
Offline
#110 31. 12. 2018 05:29 — Editoval KennyMcCormick (31. 12. 2018 05:42)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
Ale né, je to přesně naopak - definice pomocí křivového integrálu je univerzální a definice pomocí práce vyžaduje přenos (veškerého) náboje po jedné křivce.
1. Aha. Proč by definice přes práci vyžadovala přenos po jedné křivce? Resp. pokud by v případě přenosu jednotkového náboje po více křivkách neplatilo, že se práce vykonaná při přenosu jednotkového náboje rovná svorkovému napětí, jak to jde dohromady se zákonem zachování energie?
2. Předtím jsi psal (editováno pro přehlednost)
KennyMcCormick napsal(a):
1. Záporně vzatá změna indukčního toku za čas:
2. Přes křivkový integrál (stejně jako v případě DC zdrojů)
Pro definici 1 neplatí nezbytně, že svorkové napětí ideálního AC zdroje je rovno EMN (např. v případě elektronických AC zdrojů).
Pro definici 2 platí vždy, že svorkové napětí ideálního AC zdroje je rovno EMN. (Protože máme zákon zachování energie.)Pro definici 2 to neplatí taky, protože jak už jsem zmiňoval, pokud dráha proudu nebude stejná jako dráha po které počítáme integrál (např. když dráhu proudu rozvětvíme) tak to také platit nebude.
Takže tady jsem myslel, že píšeš, že se definice přes křivkový integrál nerovná svorkovému napětí v případě, že rozvětvíme dráhu proudu.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#111 31. 12. 2018 11:52
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
Ale né, je to přesně naopak - definice pomocí křivového integrálu je univerzální a definice pomocí práce vyžaduje přenos (veškerého) náboje po jedné křivce.
1. Aha. Proč by definice přes práci vyžadovala přenos po jedné křivce? Resp. pokud by v případě přenosu jednotkového náboje po více křivkách neplatilo, že se práce vykonaná při přenosu jednotkového náboje rovná svorkovému napětí, jak to jde dohromady se zákonem zachování energie?
No tak nějakou práci vykoná přece ten proud, co teče jinou cestou než skrze svorky zdroje.
Já mám pořád pocit, že si pod pojmem "zdroj" představuješ skutečný zdroj EMN (třeba akumulátor) a od něj vedoucí 2 dráty ke svorkám. Pak to samozřejmě bude vycházet stejně.
Ale zkusi si představit, že mezi vývody toho zdroje EMN bude zapojená relativně komplikovaná odporová síť - přes kterou samozřejmě bude protékat nějaký proud. A libovolné dva uzly té odporové sítě můžeme vyvést na fyzické svorky a napětí mezi nimi prohlásit za "svorkové napětí". Těch napětí může být dost velký počet - dle složitosti naší sítě. Není to ničím omezené. Nedokážu si představit, jak ze svorkového napětí určíš to EMN, bez detailní znalosti té odporové sítě.
Zatímco při použití toho smyčkového integrálu jsou jen dvě možnosti - buď smyčka prochází i tím "skutečným zdrojem EMN", potom dá integrál jeho hodnotu, a nebo jím neprochází, a potom dá nulu. Jasně, hypoteticky by jím také mohla procházet 2x nebo i vícekrát, potom by byla hodnota pochopitelně n-násobná. Ale to se dá omezit požadavky na topologii smyčky.
Offline
#112 31. 12. 2018 11:56 — Editoval MichalAld (31. 12. 2018 11:56)
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
Takže tady jsem myslel, že píšeš, že se definice přes křivkový integrál nerovná svorkovému napětí v případě, že rozvětvíme dráhu proudu.
Já jsem nikdy (doufám) nepsal, že hodnota napětí vypočtená přes křivkový integrál se rovná svorkovému napětí. Vždycky jsem (douvám) psal, že hodnota vypočtená přes křivkový integrál se rovná elektromotorickému napětí.
Svorkové napětí a definice EMN vycházející ze svorkového napětí je tvůj vynález, né můj.
Offline
#113 31. 12. 2018 12:02
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
1. Záporně vzatá změna indukčního toku za čas:
2. Přes křivkový integrál (stejně jako v případě DC zdrojů)
Pokud jde o tohle - ty dva výrazy dávají zcela identickou hodnotu - je to přímo jedna z maxwellových rovnic - v integrálním tvaru. Pochopitelně za předpokladu, že ten křivkový integrál je křivkový integrál E (a né nějakých dalších neelektrických sil). Takže takto vypočtená napětí musejí mít stejné vlastnosti.
Offline
#114 01. 01. 2019 04:43
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
Ale zkus si představit, že mezi vývody toho zdroje EMN bude zapojená relativně komplikovaná odporová síť - přes kterou samozřejmě bude protékat nějaký proud. A libovolné dva uzly té odporové sítě můžeme vyvést na fyzické svorky a napětí mezi nimi prohlásit za "svorkové napětí". Těch napětí může být dost velký počet - dle složitosti naší sítě. Není to ničím omezené. Nedokážu si představit, jak ze svorkového napětí určíš to EMN, bez detailní znalosti té odporové sítě.
Myslíš to tak, že ke zdroji je připojená odporová síť a k odporové síti svorky, takže můžu měnit svorkové napětí posouváním svorek?
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#115 01. 01. 2019 13:32
#116 02. 01. 2019 07:26
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
Aha, tj. něco takového, takže by proud procházel jednak obvodem (ve směru modré šipky  ) a jednak odporem (skrz
) a jednak odporem (skrz 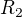 shora dolů)?
shora dolů)?
V tom případě zdroj + odporová síť je zdroj, který nás zajímá. Řekl bych, že autoři definice "práce vykonaná při přenosu jednotkového náboje" měli na mysli práci vykonanou při přenosu na okruhu první svorka zdroje -> obvod -> druhá svorka zdroje -> zdroj -> první svorka zdroje, tj. za "práci" považují práci vykonanou na přenos náboje tímhle okruhem. Energie ztracená na přenos náboje uvnitř zdroje opačným směrem (skrze 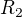 ) by byly v tomto kontextu "ztráty".
) by byly v tomto kontextu "ztráty".
Tj. "vykonaná práce na přenos jednotkového náboje" by byla vlastnost obvodu jako takového, a ne nějaké konkrétní křivky. (Byť vím, že v širší rovině je "práce elektrického proudu" pojem aplikovatelný na každý elektrický proud, ne jenom na ten, na kterém je konána pro nás užitečná práce.)
Teď je tedy otázka, zda pod takovým chápáním vykonané práce můžeme říct, že práce vykonaná při přenosu jednotkového náboje je rovna svorkovému napětí, což myslím, že je (kvůli zákonu zachování energie).
Dává to smysl, nebo jsem tě pochopil špatně?
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#117 02. 01. 2019 17:15
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
Řekl bych, že autoři definice "práce vykonaná při přenosu jednotkového náboje" měli na mysli ...
Řekl bych, že když už si někdo dá tu práci aby vymyslel nějakou definici, měl by ji vymyslet tak, aby dávala smysl. Pokud se musí používat úvahy typu "autoři měli nespíš na mysli že..." - no tak je to definice naprd.
U lineárních obvodů platí také (určitě to víš) Théveninova věta - každý lineární obvod lze nahradit zdrojem napětí a sériovým odporem. A vůbec nic špatného se nestane, když řekneme že každý obvod lze nahradit zdrojem elektromotorického napětí a sériovým odporem.
Tak nějak mi přijde, že to je to, k čemu se snažíš celou dobu nějak dobrat - že EMN uvnitř komplikovaného zdroje lze nějak "definovat" tak, aby vyšlo to EMN ekvivalentního náhradního zdroje - čili napětí zdroje naprázdno.
V rámci teorie obvodů je to určitě možné, z fyzikálního hlediska je to podle mě nesmysl. EMN je důsledkem fyzikálního procesu, který poskytuje (nepřetržitě) tu energii. Nevidím nejmenší důvod proč by EMN mělo nějak záviset na součástkách co navěsíme kolem toho.
Dále - věta platí jen v lineárních obvodech (i ve střídavých), ale máme také nelineární prvky (diody např.). A tam už to takhle není.
Offline
#118 03. 01. 2019 06:32
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
Jestli jsem pochopil tvůj příspěvek správně, tak píšeš, že:
1. Můžeme chápat práci tak, aby práce vykonaná při přenosu jednotkového náboje byla rovna napětí na svorkách, ale je to zbytečně nepřirozené chápání pojmu práce.
2. V lineárních obvodech můžeme definovat EMN tak, aby bylo rovno napětí zdroje naprázdno.
(Jestli jsem to špatně pochopil, tak mě oprav.)
Co se týče bodu 2. - máš na mysli tu definici EMN přes práci vykonanou při přenosu jednotkového náboje?
Další otázka: V případě nelineárních obvodů, pokud budu práci vykonanou na proudu, který nepřispívá k přenosu náboje obvodem (jako je ten, který na obrázku z předchozího komentáře prochází odporem 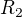 ), považovat za ztráty (a ne za vykonanou práci), bude vykonaná práce rovna svorkovému napětí?
), považovat za ztráty (a ne za vykonanou práci), bude vykonaná práce rovna svorkovému napětí?
(Je intuitivně jasné, jakou práci myslím, nebo je potřeba to rigorózně definovat?)
EMN je důsledkem fyzikálního procesu, který poskytuje (nepřetržitě) tu energii. Nevidím nejmenší důvod proč by EMN mělo nějak záviset na součástkách co navěsíme kolem toho.
Protože jenom část té energie koná práci. Pokud připojíš další součástky a výsledný systém použiješ jako zdroj, tvůj nový zdroj bude "původní zdroj + součástky", což je fyzikální systém, který nemusí nezbytně vykonat tutéž práci jako původní zdroj.
Takže pokud budeme, jako moje učebnice, definovat EMN vykonanou prací, může se změnit EMN.
V tomhle případě např. - pokud  a (jako limitní případ)
a (jako limitní případ) 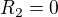 , pak je napětí na svorkách nulové, takže pokud připojím ideální vodič na svorky a bude procházet proud, tak práce vykonaná elektromotorickými silami je rovna nule (protože mezi 2 body vyvedenými na svorky není žádné elektrostatické napětí, které by elektromotorické síly musely překonávat).
, pak je napětí na svorkách nulové, takže pokud připojím ideální vodič na svorky a bude procházet proud, tak práce vykonaná elektromotorickými silami je rovna nule (protože mezi 2 body vyvedenými na svorky není žádné elektrostatické napětí, které by elektromotorické síly musely překonávat).
Vykonaná práce při přenosu jednotkového náboje je tedy nula. Přidáním jednoho odporu (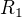 ) a jednoho vodiče se tak změnila práce vykonaná při přenosu jednotkového náboje.
) a jednoho vodiče se tak změnila práce vykonaná při přenosu jednotkového náboje.
Takže část toho důvodu, proč jsi psal, že práce nemusí být rovna svorkovému napětí, je ten, že jsi práci definoval jako práci elektrického proudu. Teď zbývá odhalit, jestli spolu nesouhlasíme i z jiného důvodu (např. jestli jsem něco napsal špatně), nebo jestli to byl jenom terminologický rozdíl. 🙂
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#119 03. 01. 2019 17:40 — Editoval MichalAld (03. 01. 2019 17:42)
Re: Různé napětí - stejný proud?
KennyMcCormick napsal(a):
Protože jenom část té energie koná práci. Pokud připojíš další součástky a výsledný systém použiješ jako zdroj, tvůj nový zdroj bude "původní zdroj + součástky", což je fyzikální systém, který nemusí nezbytně vykonat tutéž práci jako původní zdroj.
No a to je podle mě špatně.
Z pohledu fyziky je celkem jedno, jesti ty součástky považujeme za "část zdroje" a energii, která se na nich promění v teplo označíme za "ztráty zdroje" nebo jestli součástky považujeme za "spotřebič" a energii jež se na nich propálí budeme považovat za "vykonanou práci". Nebo cokoliv mezi tím.
Podstatný je ten fyzikální mechanismus poskytující energii, ať už se pak změní ve "ztráty" nebo "vykonanou práci" nebo obojí. A EMN by mělo být vlastností toho mechanismu, né těch součástek za tím (ať už je počítáme do zdroje nebo né).
Pokud na to máš jiný názor, já ti ho neberu. Až dodnes jsem žil bez toho, že bych vůbec věděl, co to nějaké EMN je, a nijak zvlášť mi to nechybělo.
Ale přijde mi neobyčejně kouzelné, že lze tohle EMN určit pomocí křivkového integrálu nezávisle na té kupě součástek, kterou k tomu připojíme.
Pokud chceš mít EMN závislé na těch součástkách, proč né, ale mohlo by se to nazývat třeba náhradní EMN, nebo EMN náhradního zdroje. A nebo prostě jen "napětí naprázdno" - stejně se to tak dělá.
Pokud chceš definici skrze práci - měla by to být práce SPOTŘEBOVANÁ zdrojem, né "vykonaná". Jenže u zdroje, který obnáší svůj vnitřní odběr (ztráty) skrze tu síť těch součástek, bychom ty ztráty museli znát. A pak to na základě jejich znalostí nějak složitě definovat. Zatímco smyčkový integrál - tomu je to všechno jedno. Proto se mi to líbí - na ničem to nezávisí.
Offline
#120 04. 01. 2019 16:24
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
Protože jenom část té energie koná práci. Pokud připojíš další součástky a výsledný systém použiješ jako zdroj, tvůj nový zdroj bude "původní zdroj + součástky", což je fyzikální systém, který nemusí nezbytně vykonat tutéž práci jako původní zdroj.
No a to je podle mě špatně.
Z pohledu fyziky je celkem jedno, jesti ty součástky považujeme za "část zdroje" a energii, která se na nich promění v teplo označíme za "ztráty zdroje" nebo jestli součástky považujeme za "spotřebič" a energii jež se na nich propálí budeme považovat za "vykonanou práci". Nebo cokoliv mezi tím.
Podstatný je ten fyzikální mechanismus poskytující energii, ať už se pak změní ve "ztráty" nebo "vykonanou práci" nebo obojí. A EMN by mělo být vlastností toho mechanismu, né těch součástek za tím (ať už je počítáme do zdroje nebo né).
Můžeme definovat EMN tak, aby nemohlo být změněno ani pasivními součástkami, ani tím, kde ke zdroji připojíme svorky, ale v takovém případě to bude jiné EMN než u těch autorů učebnice, kteří napsali tu větu, že EMN je rovno svorkovému napětí zdroje naprázdno (je vidět z toho odvození, že integrují po cestě, která vede skrz zdroj mezi svorkami, takže to, jestli je někde mimo tu cestu nějaká další část zdroje napětí, která působí na náboje elektromotorickou silou způsobem "mimo" ten obvod, podél kterého integrují, se do výsledku už neprojeví (je to vidět na tom příkladu v minulém příspěvku s  a
a 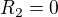 , kde dostanu nulové EMN, protože mezi svorkami skrze zdroj nekonají elektromotorické síly žádnou práci (protože to není potřeba, když mezi těmi dvěma body nepůsobí žádná elektrostatická síla)).
, kde dostanu nulové EMN, protože mezi svorkami skrze zdroj nekonají elektromotorické síly žádnou práci (protože to není potřeba, když mezi těmi dvěma body nepůsobí žádná elektrostatická síla)).
Myslím, že jsem to už pochopil.
(Mně je jasné, že ta definice, která bere v úvahu jenom "zdroj" jako takový, je určitě lepší.)
Jestli jsem to správně pochopil, tak to byl jenom rozdíl v sémantice (a v tom, která definice má praktický smysl, protože když definovali EMN tak, aby platila věta, že EMN je ekvivalentní napětí naprázdno, tak ta definice může být zbytečná), takže to asi můžeme uzavřít. 🙂
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#121 04. 01. 2019 22:55
Re: Různé napětí - stejný proud?
No jo, asi už toho necháme.
Já sice nechápu, jak mohli (u zdroje doplněného nějakými odpory, kterými protéká proud) provádět integraci (předpokládám že integraci E a analogických neelektrických veličin) a dostat při tom napětí na svorkách (naprázdno) a zároveň procházet tím vnitřním skutečným zdrojem EMN - protože podle mě to není možné, ale co, svět se asi kvůli tomu nezhroutí.
Offline
#122 04. 01. 2019 23:11
Re: Různé napětí - stejný proud?
Já bych řek, že je to důsledek souhry historických okolností:
- V okolním světě používají eletromotorickou sílu a proto je ani nenapadne to cpát někam do obvodů místo napětí a tak to používají jen tam, kde je k tomu vážný důvod.
- U nás vymysleli vhodnější termín, který se jako napětí používat dá a učitelům se zalíbil (prostě další termín, ze kterého se dá snadno zkoušet), tak ho začali cpát všude.
Celkově mi přijde, že na učivu nižších stupňů (nevím zda jen našich) škol je do značné míry vidět, že optimalizace pro snadné zkoušení převažuje nad praktickou použitelností.
Offline
#123 06. 01. 2019 16:23
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Různé napětí - stejný proud?
Já sice nechápu, jak mohli (u zdroje doplněného nějakými odpory, kterými protéká proud) provádět integraci (předpokládám že integraci E a analogických neelektrických veličin)
Ale ne, já jsem myslel to první odvození z té knihy, kterou jsem tu fotil předtím. Na koncích zdroje jsou dva náboje vytvářející elektrostatické pole, vnitřkem (odpojeného) zdroje neprotéká proud, takže když budu integrovat elektromotorickou intenzitu vnitřkem zdroje, dostanu napětí na svorkách (protože když integruju elektrostatickou intenzitu, taky dostanu napětí na svorkách). Tam odpor nebyl explicitně součástí zdroje.
Já sice nechápu, jak mohli (u zdroje doplněného nějakými odpory, kterými protéká proud) provádět integraci (předpokládám že integraci E a analogických neelektrických veličin) a dostat při tom napětí na svorkách (naprázdno) a zároveň procházet tím vnitřním skutečným zdrojem EMN
Když si vezmeme ten příklad tady, a  a
a 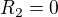 , tak svorkové napětí bude
, tak svorkové napětí bude 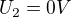 ,
, 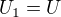 . Když budeme integrovat práci vykonanou vnějšími silami na jednotkovém náboji a půjdeme skrz "skutečný" zdroj, dostaneme
. Když budeme integrovat práci vykonanou vnějšími silami na jednotkovém náboji a půjdeme skrz "skutečný" zdroj, dostaneme  , potom projdeme odporem
, potom projdeme odporem 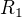 a dostaneme
a dostaneme 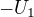 , takže celková práce vykonaná vnějšími silami na jednotkovém náboji při integraci "celým" zdrojem bude
, takže celková práce vykonaná vnějšími silami na jednotkovém náboji při integraci "celým" zdrojem bude 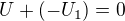 . Naproti tomu, pokud budu integrovat jenom skrz (nulový) odpor
. Naproti tomu, pokud budu integrovat jenom skrz (nulový) odpor 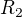 , dostanu taky práci vnějších sil rovnu nule (protože tam není žádné elektrostatické pole, které by vnější síly musely přemáhat (není tam napětí)).
, dostanu taky práci vnějších sil rovnu nule (protože tam není žádné elektrostatické pole, které by vnější síly musely přemáhat (není tam napětí)).
Takže ať už jsem integroval skrz "skutečný" zdroj, nebo ne, dostal jsem stejnou hodnotu vykonané práce (tj. 0 J), což odpovídá tomu, že je nulové svorkové napětí.
Dává to smysl, nebo jsem něco někde napsal špatně?
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
