Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 30. 12. 2018 18:34
Re: Vyjádření neznámé
↑ zzzz1:
A ptát se na důvod, proč nějaký matematický problém (třeba rovnici) nelze analyticky vyřešit je trochu nesmyslná otázka. Většina rovnic, které dokážeme vymyslet, NEMÁ analytické řešení. Jen velmi speciální případy jej mají. Akorát že ve škole se setkáváš jen s těmi speciálními případy - takže si možná myslíš, že i všechny ostatní rovnice jdou takto jednoduše vyřešit - jenže to tak není.
Můžeš na to také koukat tak, že namísto rovnice si to napíšeš jako funkci, třeba 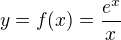
a ty chceš najít tzv. inverzní funkci, tj 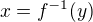
Ale teď je otázka, jestli se ti podaří vyjádřit tuto novu funkci jako nějakou kombinaci funkcí, které už znáš (sčítání, násobení, mocnění, exponenciální fce, logaritmy, goniometrické funkce atd).
Ve většíně případů se ti to nepodaří - funkcí je nekonečné množství, takže si lze myslím celkem snadno představit, že je asi nejde všechny poskládat z několika základních.
Offline

 z rovnice
z rovnice 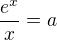 . Pokud to nejde tak by mě zajímal důvod.
. Pokud to nejde tak by mě zajímal důvod.
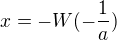 kde
kde